九年级(上)数学期末摸拟测试题
一、填空题（每小题3分，共36分）
1、方程 x 2 = x 的解是______________________
2、若
，则
_________。
3、圆和圆有不同的位置关系.与下图不同的圆和圆的位置关系是_____.(只填一种)
 |
4、若方程kx2–6x+1=0有两个实数根，则k的取值范围是 .
5、已知函数
的图象关于y轴对称，则m＝________；
6、已知一条弧的长是3
厘米, 弧的半径是6厘米,则这条弧所对的圆心角是 度
7、形状与
的图象形状相同，但开口方向不同，顶点坐标是（0，5）的抛物线的解析式 。
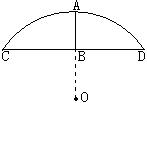
8、如图，有一圆弧形门拱的拱高AB为1m，跨度CD为4m，则这个门拱的半径为 m。
9、二次函数
与一次函数
只有唯一公共点，则
_______
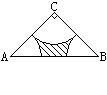10、如图，在Rt△ABC中，∠C=90°，CA=CB=2。分别以A、B、C为圆心，以
AC为半径画弧，三条弧与边AB所围成的阴影部分的面积是______.
11、已知：如图，等腰三角形ABC中，AB=AC=4，若以AB为直径的⊙O与BC相交于点D，DE∥AB，DE与AC相交于点E，则DE=____________。
12、若实数a、b满足
，则a+b的值为________．
二、选择题（每小题4分，共20分）
13、要使二次根式
有意义，那么x的取值范围是（ ）
（A）x＞－1 （B） x＜1 （C） x≥1 （D）x≤1
14、下列几个图形是国际通用的交通标志，其中不是中心对称图形的是（ ）
A B C D
15、有6张写有数字的卡片，它们的背面都相同，现将它们背面朝上（如图），从中任意选一张是数字3的概率是（ ）
A、
B、
C、 D、
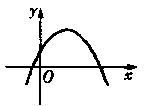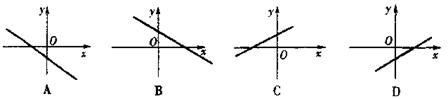
16、已知函数
的图象如图所示，则函数
的图象是（ ）
 |
三、解答题
18、（6分）计算：．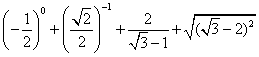 
19、解下列一元二次方程：（每题6分，共12分）
（1）、
（配方法） （2）、
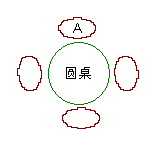
20、（6分）一张圆桌旁有四个座位，A先坐在如图所示的座位上，
B、C、D三人随机坐到其他三个座位上。求A与B不相邻而坐的概率。
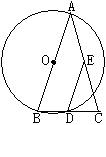
21、（8分）如图，四边形ABCD内接于⊙O，并且AD是⊙O的直径，
C是弧BD的中点，AB和DC的延长线交⊙O外一点E.求证：BC=EC.
22、（8分）一个小球以10m/s的速度在平坦地面上开始滚动，并且均匀减速，滚动20m后小球停下来．（1）小球滚动了多少时间?（2）平均每秒小球的运动速度减少多少?
（3）小球滚动到5m时约用了多少时间（精确到0.1s）?
23、（10分）如图，已知抛物线过点A(―1,0)、B(4,0)、
(1) 求抛物线对应的函数关系式及对称轴；
(2) 
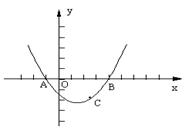点C′是点C关于抛物线对称轴的对称点，证明直线
必经过点C′。
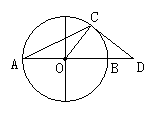
24、（10分）如图，AB为⊙O的直径，C是⊙O上一点，D在AB的延长线上，且∠DCB=∠A．
（1）CD与⊙O相切吗？如果相切，请你加以证明，如果不相切，请说明理由．
（2）若CD与⊙O相切，且∠D=30°，BD=10，求⊙O的半径．
25、（10分）某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价一元，日销售量将减少20千克。
（1）现要保证每天盈利6000元，同时又要让顾客得到实惠，那么每千克应涨价多少元？
（2）若该商场单纯从经济角度看，那么每千克应涨价多少元，能使商场获利最多。
26、（12分）数学活动小组接受学校的一项任务：在紧靠围墙的空地上，利用围墙及一段长为6０米的木栅栏围成一块生物园地，请设计一个方案使生物园的面积尽可能大．
(1)活动小组提交如图的方案。设靠墙的一边长为 x 米，则不靠墙的一边长为(60－2x)米，面积y= (60－2x) x米2．当x=15时，y最大值 =450米2．
(2)机灵的小明想：如果改变生物园的形状，围成的面积会更大吗？请你帮小明设计两个方案，要求画出图形，算出面积大小；并找出面积最大的方案．
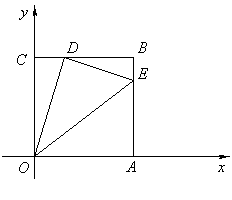
27、（12分）如图，边长为4的正方形OABC的顶点O为坐标原点，点A在x轴的正半轴上，点C在y轴的正半轴上．动点D在线段BC上移动（不与B，C重合），连接OD，过点D作DE⊥OD，交边AB于点E，连接OE．
（1）当CD=1时，求点E的坐标；
（2）如果设CD=t，梯形COEB的面积为S，那么是否存在S的最大值？若存在，请求出这个最大值及此时t的值；若不存在，请说明理由．
