九年级（上）数学期末模拟试卷2
_____班学生________成绩_____
一选择题：（每道小题3分，共30分）
1.下列等式一定成立的是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
2.时钟上的分针匀速旋转一周需要60min则经过10min，分针旋转了 （ ）
A、100 B、200 C、300 D、600
3.平面直角坐标系内一点P（－2,3）关于原点对称点的坐标是 （ ）
A、（3，－2） B、（2,3） C、（－2，－3） D、（2，－3）
4.若式子
有意义，则x的取值范围为（ ）
（A）x≥2 （B）x≠3 （C）x≥2或x≠3 （D）x≥2且x≠3
5.关于x的一元二次方程kx2-6x+1=0有两个不相等的实数根,则k 的取值范围是( )
A. k≥9
B. k<9;
C. k≤9且k≠0 D.
k<9且k≠0
6.下列图形中，既是轴对称图形又是中心对称图形的是（ ）
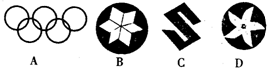图1
图2
7.如图2所示,EF为⊙O的直径,OE=5cm,弦MN=8cm,那么E、F两点到直线MN的距离之和等于 ( )
A. 12cm B. 8cm C. 6cm D. 3cm
8.下面是李刚同学在一次测验中解答的填空题，其中答对的是（ ）．
A、若x2=4，则x＝2 B、方程x(2x－1)＝2x－1的解为x＝1
C、若x2+2x+k=0的一个根为1，则
D、若分式
的值为零，则x＝1，2
9..关于
的一元二次方程
的一个根是0，则
的值为（ ）
A、1 B 、-1 C、1或-1 D、0.5
10.已知在⊙O中，弦AB的长为8厘米,圆心O到AB的距离为3厘米, 则⊙O的半径是（
）
A.3厘米 B. 4厘米 C. 5厘米 D. 8厘米
二.填空：（每小题3分，共24分）
1.若 
，则 
。
2.最简根式
和
是同类根式，则a=__________，b=__________．
3.AB是⊙O直径，AB=4，F是OB中点，弦CD⊥AB于F，则CD=_________
4.如图所示，下列各图中， 绕一点旋转1800后能与原来位置重合。
5..如图，AB是⊙O的直径，弦CD垂直平分OB，则∠BDC=__________ （5题）
6.△ABC内接于⊙O，∠ACB＝36°，那么∠AOB的度数为__________
7.三角形两边长分别为3和6，第三边是方程
的解，则这个三角形的周长是___。
8.口袋中放有3只红球和11只黄球，这两种球除颜色外没有任何区别，随机从口袋中任取一只球，取得黄球的概率是_________．
三、解答题：（每小题4分，共24分）
1.、解下列方程：
（1）用直接开平方法解方程：
（2）用配方法解方程：
（3）解方程: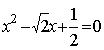 
2.计算题：
（1）．
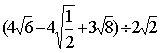（2）． 
3.、如图，画出△ABC关于原点O对称的△A1B1C1，并求出点A1，B1，C1的坐标。
 |
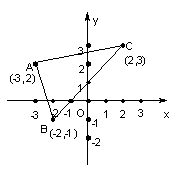四、(本题6分) 如图，在Rt△ABC中，∠B=90°，∠A的平分线交BC于D，E为AB上一点，DE=DC，以D为圆心，以DB的长为半径画圆。
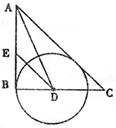求证：（1）AC是⊙D的切线；
（2）AB+EB=AC。
五 （本题4分）如图是从一副扑克牌中取出的两组牌，分别是黑桃1、2、3、4和方块1、2、3、4，将它们背面朝上分别重新洗牌后，从两组牌中各摸出一张，那么摸出的两张牌的牌面数字之和等于5的概率是多少？请你用列举法（列表或画树状图）加以分析说明．
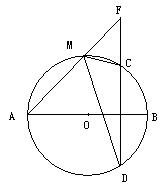六：(本题6分)已知：⊙O的直径AB和弦CD，且AB⊥CD于E，F为DC延长线上一点，连结AF交⊙O于M。求证：∠AMD＝∠FMC。
七、 (本题6分)某商场销售一批名牌衬衣,平均每天可售出20件,每件衬衣盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施. 经调查发现,如果每件衬衣降价1元,商场平均每天可多售出2件.
(1)若商场平均每天盈利1200元,每件衬衣应降价多少元?
(2)若要使商场平场每天的盈利最多,请你为商场设计降价方案.