九年级期末数学模拟试卷（2）

第一学期

九年级期末数学模拟试卷（2）

班级　　　　　　 　姓名　　　　　　 　成绩　　　　　　　　　

一、填空题（1----6题每题3分，7----10题每题4分满分34分）

1. 的平方根是　　　　 ；的算术平方根是　　　　  ；二次根式有意义，x的变化范围是　　　　　 。

2、直接写出答案：；＝　　　　

3、下列二次根式中，与是同类二次根式的是（　　　）。

A、　　 B、　　C、　　 D、

4、下列一元二次方程中，两根之和为2的是（　　）

A、　B、　C、　D、

5.若 ，则 　　　　　　　 。

6．方程的解是　　　　　　　　　 。

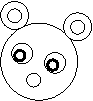
7．两圆的位置关系有多种，图中的卡通形象中不存在

的位置关系是　　　　　 。

8．在汉语拼音“SHUXUE”（数学）中任意选择一个字母，则字母为“U”的概率等于　　　　　 。

9、已知m是方程x²－x－1＝0的一个根，则代数式m²－m的值等于　　　　　  。

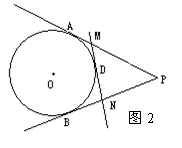10.如图，直线PA、PB、MN分别与⊙O相切于点A、B、D，若PA=PB＝8cm，则△PMN的周长是　　　　　　　 。

二、选择题：本大题共6小题，每小题4分，计24分。在每小题给出的四个选项中，只有一项是符合题目要求的。

11.平面直角坐标系内一点P（－2,3）关于原点对称点的坐标是　　　　　（　　）

A、（3，－2）　　　　B、（2,3）　　　 　C、（－2，－3）　　　D、（2，－3）

12.关于的一元二次方程的一个根是0，则的值为（　　　）

（A）1　　　　　 （B）　-1　　　 （C）1或-1　　　　（D）0.5

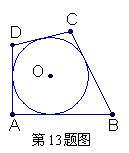
13．如图，一圆内切四边形ABCD，且AB=16，CD=10，

则四边形的周长为（　　）

A．50　　　　　　　B．52　　　　　　　 C．54　　　　　D．56

14. ⊙O的半径为5cm，弦AB//CD，且AB=8cm,CD=6cm,则AB与CD之间的距离为(　　 )

(A ) 1 cm　 (B ) 7cm　C．　3 cm或4 cm　 D． 1cm 或7cm

15．某种冰淇淋纸筒为圆锥形，其底面半径为3cm，母线长为8cm，则制作这个纸筒纸片的面积（不计加工余料）为（　　  ）

　  A．24cm²　　B．48cm²　　C．30cm²　　D．36cm²

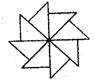
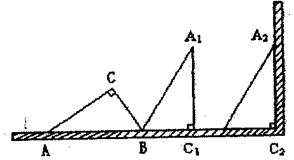
16. 如图：图可以看作是一个等腰直角三角形旋转若干次而生成的，

则每次旋转的度数可以是  （　　 ）。

A、90⁰  B、60⁰ C、45⁰ D、30⁰

三、解答题：本大题共10小题，计92分。解答应写出说理、证明过程或演算步骤

17、（每题3分，共计6分）计算下列各式：

⑴、　　　　　　　　  ⑵、

18、解方程：

19、已知关于x的一元二次方程。

　  (I)求证方程有两个不相等的实数根：

　  (2)设的方程有两根分别为日满足 求k的值。

20.如图，在一个横断面为Rt△ABC的物体中，∠ACB＝90°，∠CAB＝30°，BC＝1米，工人师傅要把此物体搬到墙边，先将AB边放在地面（直线l）上，再按顺时针方向绕点B翻转到△A₁BC₁位置（BC₁在l上），最后沿BC₁的方向平移到△A₂B₂C₂的位置，其平移的距离为线段AC的长度(此时A₂C₂恰好靠在墙边)。

（1）请直接写出AB、AC的长；

（2）画出在搬动此物的整个过程中，A点所经过的路径，并求出该路径的长度。

21.如图，OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点，BP的延长线交⊙O于点Q，过点Q的⊙O的直线交OA延长线于点R，且RP＝RQ

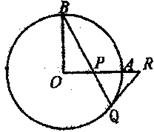（1）求证：直线QR是⊙O的切线；

（2）若OP＝PA＝1，试求RQ的长

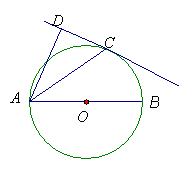22、(8分)如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．

（1）　　求证：AD⊥DC；

（2）　　若AD＝ ，AC＝2，求AB的长．

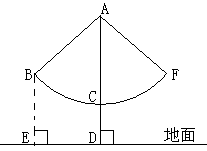23、（本题8分）如图，秋千拉绳长AB为3米，静止时踩板离地面0.5米，某小朋友荡该秋千时，秋千在最高处时踩板离地面2米(左右对称)，请计算该秋千所荡过的圆弧长(结果保留π)

 

24 (本题8分)某商场销售一批名牌衬衣,平均每天可售出20件,每件衬衣盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施. 经调查发现,如果每件衬衣降价1元,商场平均每天可多售出2件.

　　(1)若商场平均每天盈利1200元,每件衬衣应降价多少元?

(2)若要使商场平场每天的盈利最多,请你为商场设计降价方案.

25、田忌赛马是一个为人熟知的故事．传说战国时期，齐王与田忌各有上、中、下三匹马，同等级的马中，齐王的马比田忌的马强．有一天，齐王要与田忌赛马，双方约定：比赛三局，每局各出一匹，每匹马赛一次，赢得两局者为胜．看样子田忌似乎没有什么胜的希望，但是田忌的谋士了解到主人的上、中等马分别比齐王的中、下等马要强 … …

( 1 )如果齐王将马按上中下的顺序出阵比赛，那么田忌的马如何出阵，田忌才能取胜？ ( 2 )如果齐王将马按上中下的顺序出阵，而田忌的马随机出阵比赛，田忌获胜的概率是多少？（要求写出双方对阵的所有情况）

26．（本题满分8分）

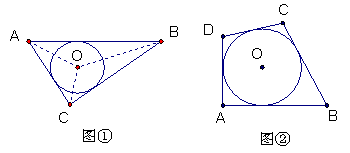
阅读材料：如图①，△ABC的周长为，内切圆O的半径为r,连结OA、OB、OC，△ABC被划分为三个小三角形，用表示△ABC的面积。

∵

又∵, ,

∴++= (可作为三角形内切圆半径公式)

（1）　  理解与应用：利用公式计算边长分为5、12、13的三角形内切圆半径；

（2）类比与推理：若四边形ABCD存在内切圆(与各边都相切的圆，如图②)且面积为S，各边长分别为a、b、c、d，试推导四边形的内切圆半径公式；（要写推导过程）

（3）拓展与延伸：若一个n边形(n为不小于3的整数)存在内切圆，且面积为S，各边长分别为、、、… 、，合理猜想其内切圆半径公式(不需说明理由)．

 27、设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为d．

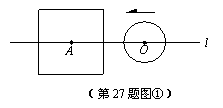
（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：

d、a、r之间关系	公共点的个数
d＞a＋r
d＝a＋r
a－r＜d＜a＋r
d＝a－r
d＜a－r

所以，当r＜a时，⊙O与正方形的公共点的个数可能有　　　　　　　　　个；

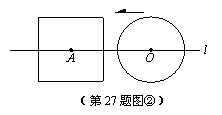
（2）如图②，当r＝a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：

d、a、r之间关系	公共点的个数
d＞a＋r
d＝a＋r
a≤d＜a＋r
d＜a

所以，当r＝a时，⊙O与正方形的公共点个数可能有　　　　　　　　个；

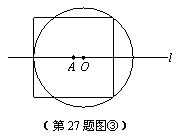（3）如图③，当⊙O与正方形有5个公共点时，试说明r＝a；

（4）就r＞a的情形，请你仿照“当……时，⊙O与正方形的公共点个数可能有　　　　　　　个”的形式，至少给出一个关于“⊙O与正方形的公共点个数”的正确结论．

（注：第（4）小题若多给出一个正确结论，则可多得2分，但本大题得分总和不得超过12分）