九年级数学第一学期期末模拟测试
数 学 试 卷
（时间：120分钟 满分：150分）
一，填空题
1. 化简：
2. 方程
的解是
3．一颗正方体骰子，六个面上的数字分别为1、2、3、3、4、5，投掷一次，向上的面出现数字为3的概率为_____________
4. 当
时，二次根式
在实数范围内有意义.
5. 如图，自行车的两个车轮看作两个圆，则这两个圆的位置
关系是 .
6. 任意写一个一元二次方程，使得这个方程有两个相等的
实数根，你举的方程是 .
7. 如图，在“扫雷”游戏中，“
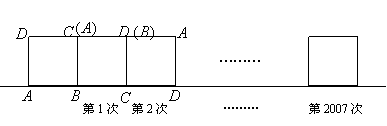8. 如图，将一块正方形的木板
沿水平线上连续向右翻滚2007次后，落在如图所示的位置上，请在相应的图中标出正方形四个顶点
、
、
、
的位置.
9.观察下列各式：=2, =3,=4,……请你
将猜想到的规律用含自然数n(n≥1)的代数式表示出来是
.
10．二次函数y＝ ax2 ＋ bx＋ c 的图象如图所示，试根据图象回答：，当x满足条件 时，y＞0．
二 选择题（每题4分，共计24分）
11. 下列图形中不是中心对称图形的是
（A） （B） （C） （D）
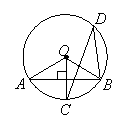12. 根据电视台天气预报：将乐明天降雨的概率为
％，对此信息，下列几种说法中正确的是
（A）将乐明天一定会下雨
（B）将乐明天有％的地区会降雨
（C）将乐明天有％的时间会降雨
（D）将乐明天下雨的可能性很大
13. 如图，、、、四点都在⊙
上，若
，
，则圆周角
的度数等于
（A）
（B）
（C）
（D）
14. 若
是方程
的一个根，则代数式
的值等于
（A）0 （B）1003 （C）2007 （D）2008
15.已知两圆的半径分别是
A．相交 B．内切 C．外切 D．外离
16. 用一个圆心角为120°，半径为
（A）
三，解答题
17. 计算：
. 18解方程：
.
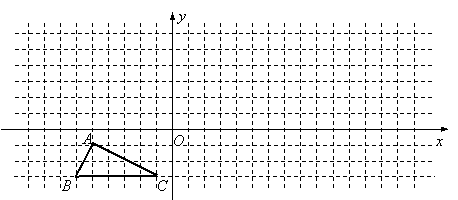
19.（10分）如图，已知△
，作如下操作：
（1）以原点为旋转中心，将△顺时针旋转90°；
（2）以原点为位似中心，将△放大为原来的2倍.
20.（10分）某银行经过最近的两次降息，使一年期存款的年利率由2.25％降至1.96％，求平均每次降息的百分率。
21. （10分）现有足够多的除颜色外都相同的球供你选用，还有一个最多只能装10个球的不透明袋子.
（1）请你设计一个摸球游戏，使得从袋中任意摸出1个球，摸得红球的概率为
，则应往袋中如何放球？ .
（2）若袋中装有2个红球和2个白球，搅匀后从袋中摸出一个球后，不放回，而后再摸出一个球，则请用列表或画树形图的方法列出所有等可能情况，并求出两次摸出的球都是红球的概率.
22. （10分）如图，以为圆心的同心圆中，大圆的弦
交小圆于点，且
，则
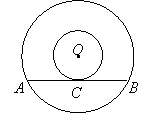（1）求证：是小圆的切线；
（2）当
时，求这个圆环的面积
.（保留
）
23． 如图，点A、B、D、E在圆上，弦AE的延长线与弦BD的延长线相交于点C.给出下列三个条件：（1）AB是圆的直径；（2）D是BC的中点；（3）AB=AC
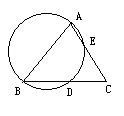请在上述条件中选择两个作为已知条件，第三个作为结论，写出一个你认为正确的命题，并加以证明.（共6分）
条件：___________________________
结论：____________________________
证明：
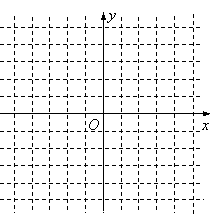
24.（10分）已知函数
.
（1）画出这个函数的图象，指出图象的
对称轴: , 顶点坐标: .
（2）利用图象，写出方程
的两根（精确到0.1）：
，
.
（3）当
时，
随的增大
而减小，若≥2，则自变量的取值范围是
.
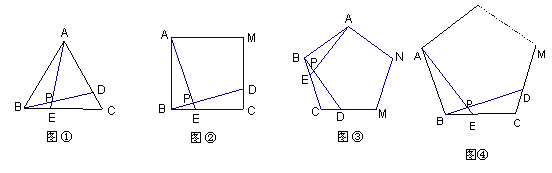
25、如图①、②、③中，点E、D分别是正△ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的相邻两边上的点，且BE = CD，DB交AE于P点．
⑴图①中，∠APD的度数为60°，
图②中，∠APD的度数为90°，
图③中，∠APD的度数为____ ____；（直接写答案）
⑵根据前面探索，将本题推广到一般的正n 边形情况．
如图④，点E、D分别是正n边形ABCM …中以C点为顶点的相邻两边上的点，且BE=CD，BD与AE交于点P，则∠APD的度数为 ．
（直接写答案）
26. 科学家把一种珍奇植物分别放在不同温度的环境中，经过一段时间后，测试出这种植物高度的增长量/mm与温度/℃的变化情况，并推测与之间是二次函数关系（如下表）：
| 温度 |
|
|
|
| 0 | 2 | 4 | 6 |
| 植物高度的 增长量 | 1 | 41 | 49 | 49 | 41 | 1 |
（1）根据表中数据，求出这个二次函数的解析式，并把表格补充完整；
（2）由此，科学家推算出最适合这种植物生长的温度是
℃，高度最多能增长
；
（3）在什么条件下，这种植物将不会增长？
27．已知：OA，OB是⊙O的半径，且OA⊥OB，P是射线OA上一点，（点A除外），直线BP交⊙O于点Q，过Q作⊙O的切线交直线OA于点E。（共10分）
（1） 如图（1），若点P在线段OA上，求证：∠OBP+∠AQE=450.
（2） 
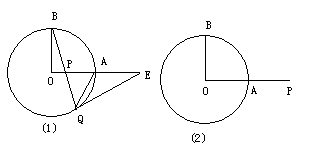若点P在线段OA的延长线上，其他条件不变，∠OBP与∠AQE之间是否存在某种确定的等量关系？请你完成图（2），并写出结论（不需要证明）