九年级数学上学期期末测试题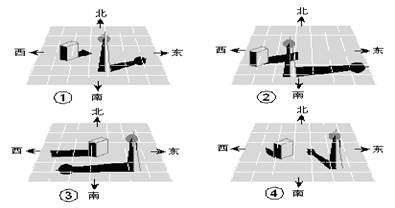
（十）
班级： 姓名： 总分：
一：填空题（每小题3分，共27分）
1．方程x(x+3)=x+3的解是 。
2．等腰三角形的两边长分别为5cm和2cm，则它的周长是________cm。
3．如图，地面A处有一支燃烧的蜡烛(长度不计)，一个人在A与墙BC之间运动，则他在墙上的投影长度随着他离墙的距离变小而 (填“变大”、“变小”或“不变”).
 |
4．点（2，
）和（－，a）都在双曲线
上，则a=
。
5．有一个面积为60的梯形，其上底长是下底长的
，若下底长为x，高为y，则y与x的函数关系式是
。
6．若四边形的两条对角线相等，则顺次连结该四边形各边中点所得的四边形是 。
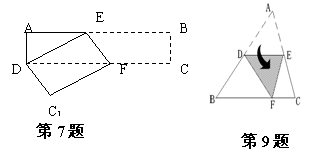
7．矩形纸片ABCD中，AD=4cm ，AB=10cm，按如图方式折叠,使点B与点D重合，折痕为EF，则DE= cm。
8．如图，D、E为△ABC两边AB、AC的中点，将△ABC沿线段DE折叠，使点A落在点F处，若∠B=55°，则∠BDF= 。
9．从边长为1，3，4，7的四条线段中任意取三条作为三边，能够成三角形的概率为 。
二：选择题（每小题4分，共28分）
| 题号 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 选项 |
10．方程（x－1）2=x－1的根是（）
A，1 B，－1 C，2 D，1或2
11．如果某物体的三视图是如图所示的三个图形，那么该物体的形状是（）
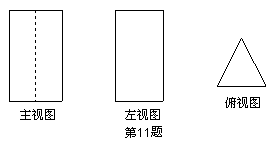A、正方体 B、长方体 C、三棱柱 D、圆锥
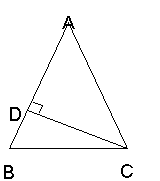
12．如图，等腰三角形ABC中，AB=AC，∠A=44°，CD⊥AB于D，则∠DCB等于（）
A、44° B、68° C、46° D、22° （2005常州）
13．对角线互相垂直平分且相等的四边形一定是（）。
A．正方形 B．菱形
C．矩形 D．等腰梯形
14．下面是一天中四个不同时刻
两个建筑物的影子：将它们按
时间先后顺序进行排列，正确
的是（）
A、③④②① B、②④③①
C、③④①② D、③①②④
15．张华同学的身高为1.6米，
某一时刻他在阳光下的影
长为2米，与他邻近的一棵树的影长为6米，则这棵树的高为（）
A、3.2米 B、4.8米 C、5.2米 D、5.6米
16．已知直角三角形的两条直角边的长恰好是方程
的两根，则此直角三角形的斜边长为()。
A.
B.3 C.
D.13
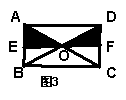17.如图3，EF过矩形ABCD对角线的交点O，且分别交AB、CD于E、F，那么阴影部分的面积是矩形ABCD的面积的（）(2005福州)
A、
B、
C、 D、
三：解答题（共65分）
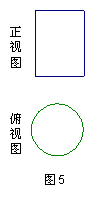18．一个物体的正视图、俯视图如图5所示，
请你画出该物体的左视图并说出该物体形状的名称. （7分）
19．解方程：x2＋5x＋3=0（5分）
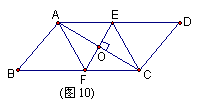20．已知：如图10，平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
求证：四边形AFCE是菱形. （7分）
21．已知：如图，四边形ABCD是菱形，E是BD延长线上一点，F是DB延长线上一点，且DE=BF。请你以F为一个端点，和图中已标明字母的某一点连成一条新的线段，猜想并证明它和图中已有的某一条线段相等（只须证明一组线段相等即可）。（2005北京）
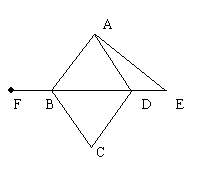（1）连结____________ ； （1分）
（2）猜想：______ =______ ；（2分）
（3）证明： （4分）
22．已知，如图8，AB和DE是直立在地面上的两根立柱.AB=5m，某一时刻AB在阳光下的投影BC=3m。（2004河南）（8分）
（1）请你在图8中画出此时DE在阳光下的投影；
（2）在测量AB的投影时，同时测量出DE在阳光下的投影长为6m，请你计算DE的长.
 |
23．（7分）年三十的团圆饭桌上，教数学的李老师给初三的儿子小祥出了一道数学题：“火锅中煮了大小、形状完全相同，颜色不同的鱼、肉两种丸子共100个。有什么办法估计其中鱼丸子和肉丸子各有多少个？”
（1）请你帮小祥设计一个方案；
（2）若试验后发现鱼、肉两种丸子的比我为13：7，则你从中任取一个丸子十余万字的概率是多少？
24．如图，已知四边形ABCD是平行四边形，∠BCD的平分线CF交边AB于F，
∠ADC的平分线DG交边AB于G。（8分）
（1）求证：AF=GB；
（2）请你在已知条件的基础上再添加一个条件，使得△EFG为等腰直角三角形,并
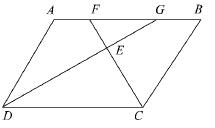说明理由．
25．（8分）某商店如果将进货价为40元的商品按每件为50元出售，每天可销售500件，现采用提高售价，减少进货量的方法增加利润，已知这种商品每涨价1元，其销售量就减少10件，问应将售价定为多少时，才能赚的8000元的利润。
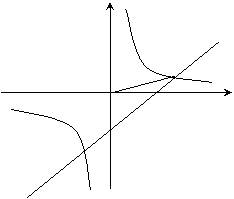
26.（8分）已知反比例函数
和一次函数y=2x－1,其中一次函数的图像经过（a,b）以及（a＋1,b＋k）两点；
（1）求反比例函数的解析式；
（2）如图，点A在第一象限，且同时在上述两个函数的图像上，求点的坐标；
（3）利用（2）得结果，请问在x轴上是否存在点P，使△AOP为等腰三角形？若存在，把符合条件的P点的坐标都求出来；若不存在，请说明理由。
|
|
|
|