九年级数学上学期期末测试题（十一）
姓名 总分
一：填空（每小题3分共15分）
1．如图，修建抽水站时，沿着倾斜角为30°的斜坡铺设管道，若量得水管AB的长度为80米，那么点B离水平面的高度BC的长为 米。
２.在△ABC中，∠A－∠C＝25°，∠B－∠A＝10°，则∠B＝ ；
 | |||
 | |||
(第3题图)
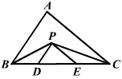
3．如图，在△ABC中，BC
，BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则△PDE的周长是 
；
4．初三(1)班共有48名团员要求参加青年志愿者活动，根据实际需要，团支部从中随机选择12名团员参加这次活动，该班团员李明能参加这次活动的概率是___ ____
5．三角形三边长为6、8、10，则这个三角形的面积是 。
二：选择（每小题3分，共30分）
| 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|
|
|
|
|
|
|
|
|
|
|
6．方程x2－x=0的根是（）
A、x=1 B、x=0 C、x1=0或x2=1 D、x1=－1或x2=1
7．顺次连结等腰梯形四边中点得到一个四边形，再顺次连结所得四边形四边的中点得到的图形是()
A、等腰梯形 B、直角梯形 C、菱形 D、矩形
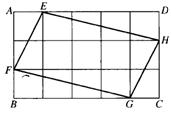
8．如图，将矩形ABCD分成15个大小相等的正方形，E、F、G、H分别在AD、AB、BC、CD边上，且是某个小正方形的顶点.若四边形EFGH的面积为1,则矩形ABCD的面积是（）
A.2
B.
C.
D.
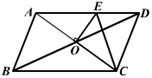
9．如图，□ABCD的周长为
，AC、BD相交于点O，
OE⊥AC交AD于E，则△DCE的周长为 （）
A.4 B.6 C.8 D.10
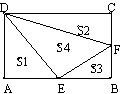10．如图，矩形ABCD长为a，宽为b，若s1=s2=
(s3+s4)，则s4等于
（ ）
（A）
（B）
（C）
（D）
11．如图是一根电线杆在一天中不同时刻的影像图，
试按其一天中发生的先后顺序排列，正确的是 （）
A、①②③④ B、④①③② C、④②③① D、④③②①
12．有一实物如图，那么它的主视图
 |
13.某种品牌的产品共5件，其中有2件次品，小王从中任取两件，则小王取到都是次品的概率是（）
A、0．5 B、0.1 C、0.4 D、0.6
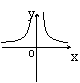
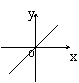
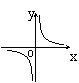
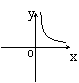
14．若矩形的面积为
，则它的长
与宽
之间的函数关系用图象表示大致（）
 |  | ||||||
 |  | ||||||
A B C D
15．从A地到C地，可供选择的方案是走水路、走陆路、走空中.从A地到B地有2条水路、2条陆路，从B地到C地有3条陆路可供选择，走空中从A地不经B地直接到C地.则从A地到C地选择的方案有（）
A、20种 B、8种 C、5种 D、13种
三：解答题（要求写出主要的步骤共75分）
16.用适当的方法解下列方程(6分)
（1）3x(x－1)=2－2x (2)x2=x＋56
17．（6分）如图：有一张三角形纸片，两直角边BC=6cm，AC=8cm，将△ABC折叠，使点A与点B重合，折痕为DE，求CE的长。
18．（6分）一个口袋内装有大小相等的1个白球和已编有不同号码的3个黑球，从中摸出2个球.
（1）共多少种不同的结果？
（2）摸出2个黑球有多少种不同的结果？
（3）摸出2个黑球的概率是多少？
19．（7分）正比例函数y=hx和反比例函数
的图象相交于A，B两点，已知点A的坐标（1，3）.写出这两个函数的表达式.
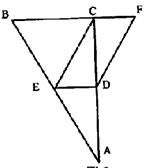
20．（7分）如图，在△ABC中∠BCA＝90°，D、E分别是AC、AB边
的中点，F在BC的延长线上。∠CDF＝∠A。
求证：四边形DECF是平行四边形。
21．（6分）某企业的年产值在两年内从1000万元增加到1210万元，求平均每年增长的百分率。
22．(5分)在∠ABC内找一点P，使它到∠ABC的两边的距离相等，并且到点A、C的距离也相等。
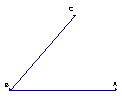
23．（8分）已知：如图，矩形AOBC，以O为坐标原点，OB，OA分别在x轴，y轴上，点A坐标为（0,3），∠OAB＝60°,以AB为轴对折后，使C点落在D点处，求D点的坐标.
24．（8分）如图，客轮沿折线A－B－C从A出发经B再到C匀速航行，货轮从AC的中点D出发沿某一方向匀速直线航行，将一批物品送达客轮。两船同时起航，并同时到达折线A－B－C的某点E处，已知AB＝BC＝200海里，∠ABC＝90°，客轮速度是货轮速度的2倍。
（1）选择：两船相遇之处E点（ ）。
A、在线段AB上 B、在线段BC上 C、可以在线段AB上，也可以在线段BC上
（2）求货轮从出发到两船相遇共航行了多少海里?（结果保留根号）。
25．（8分）在直角坐标系中，直线
与双曲线
在第一象限交于点A，在第三象限交于点D,与
轴交于点C，AB⊥轴，垂足为B，且
；
（1）求
的值；（2）求⊿ABC的面积；
26（8分）．阅读下面的题目及分析过程，并按要求进行证明．
已知：如图，E是BC的中点，点A在DE上，且∠BAE=∠CDE．
求证：AB=CD
分析：证明两条线段相等，常用的一般方法是应用全等三角形或等腰三角形的判定和性质，观察本题中要证明的两条线段，它们不在同一个三角形中，且它们分别所在的两个三角形也不全等．因此，要证AB=CD，必须添加适当的辅助线，构造全等三角形或等腰三角形．
现给出如下三种添加辅助线的方法，请任意选择其中一种，对原题进行证明．
