初升高数学试题
(满分:150分 时间:120分钟)2007-06-19
一、选择题(每小题3分,共30分)
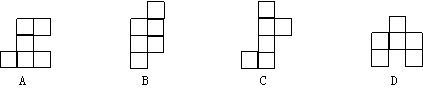
1、下面的平面图形中,是正方体的平面展开图的是 ( )
 |
2、下列计算正确的是 ( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
3、受季节影响,某种商品每年按原售价降低10%后,又降价![]() 元,现在每件售价
元,现在每件售价![]() 元,那么该商品每件的原售价为 ( )
元,那么该商品每件的原售价为 ( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
4、式子![]() 成立的条件是 ( )
成立的条件是 ( )
A、![]() ≥3 B、
≥3 B、![]() ≤1
C、1≤
≤1
C、1≤![]() ≤3
D、1<
≤3
D、1<![]() ≤3
≤3
| |
A、1个 B、2个 C、3个 D、4个
6、甲瓶盐水含盐量为![]() ,乙瓶盐水含盐量为
,乙瓶盐水含盐量为![]() ,从甲乙两瓶中各取重量相等的盐水混合制成新盐水的含盐量为 ( )
,从甲乙两瓶中各取重量相等的盐水混合制成新盐水的含盐量为 ( )
A、![]() B、
B、![]() C、
C、![]() D、随所取盐水重量而定
D、随所取盐水重量而定
7、若关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实根,则
有两个不相等的实根,则![]() 的取值范围是 ( )
的取值范围是 ( )
A、![]() B、
B、![]() ≤
≤![]() C、
C、![]() 且
且![]() ≠2 D、
≠2 D、![]() ≥
≥![]() 且
且![]() ≠2
≠2
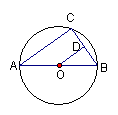
8、 如图,AB是⊙O的直径,C是⊙O上一点,若AC︰BC=![]() ︰
︰![]() ,AB=10
,AB=10![]() ,OD⊥BC于点D,则BD的长为 ( )
,OD⊥BC于点D,则BD的长为 ( )
 A、
A、![]() B、3
B、3![]() C、5
C、5![]() D、6
D、6![]()
|
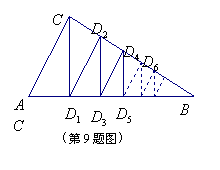
9、如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,这样继续作下去,……,线段
,这样继续作下去,……,线段![]() 等于(
等于(![]() 为正整数) ( )
为正整数) ( )
(A)
![]() (B)
(B) ![]() (C)
(C)![]() (D)
(D)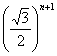
10、设![]() ,
,![]() ,
,![]() ,则
,则![]() 、
、![]() 、
、![]() 的大小关系是 ( )
的大小关系是 ( )
A、![]() <
<![]() <
<![]() B、
B、![]() <
<![]() <
<![]()
C、![]() <
<![]() <
<![]() D、
D、![]() <
<![]() <
<![]()
二、填空题(每小题3分,共36分)将答案直接写在该题目中的横线上。
11、如果反比例函数y=![]() 的图象经过点P(-3,1)那么k= _________.
的图象经过点P(-3,1)那么k= _________.
12、当![]() = 时,分式
= 时,分式![]() 的值为零。
的值为零。
13、从一个不透明的口袋中摸出红球的概率为![]() ,已知袋中的红球有3个,则袋中共有________ 个球.
,已知袋中的红球有3个,则袋中共有________ 个球.
14、已知抛物线![]() 的顶点在坐标轴上,则a=_____________.
的顶点在坐标轴上,则a=_____________.
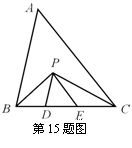
15、如图,在ΔABC中,BC=5 cm,BP、CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则ΔPDE的周长是___________ cm.
 | |||
 | |||
16、如图,正比例函数![]() (
(![]() >0)与反比例函数
>0)与反比例函数![]() 的图像交于A、C两点,AB⊥
的图像交于A、C两点,AB⊥![]() 轴于B,CD⊥
轴于B,CD⊥![]() 轴于D,则
轴于D,则![]() =
。
=
。
17、 已知![]() 。则分式
。则分式![]() 的值为
。
的值为
。
18、过⊙O内一点M的最长弦长为10cm,最短弦长为8cm,那么OM的长为___________________cm.
19、在不等边三角形ABC中,点D是AC上一点(不与A,C重合),用过点D的直线截三角形ABC,所截得的三角形与原三角形相似,则满足条件的直线最多有___________条.
 20、在半径为50cm的圆形铁皮上剪去一块扇形铁皮,用剩余部分制做成一个底面直径为80cm,母线长为50cm的圆锥形烟囱帽(如图),则剪去的扇形的圆心角的度数为_________________.
20、在半径为50cm的圆形铁皮上剪去一块扇形铁皮,用剩余部分制做成一个底面直径为80cm,母线长为50cm的圆锥形烟囱帽(如图),则剪去的扇形的圆心角的度数为_________________.
21、已知![]() ,则直线
,则直线![]() 与 坐标轴围成的三角形面积为
。
与 坐标轴围成的三角形面积为
。
三、解答题(共87分)
22、 (本题12分)(1)分解因式:![]() .
.
(2)化简:![]()
23、(本题6分)小李通过对某地区1998年至2000年快餐公司发展情况的调查,制成了该地区快餐公司个数情况的条形图如图所示,和快餐公司盒饭年销量的平均数情况条形图,利用这些信息解答下列问题:
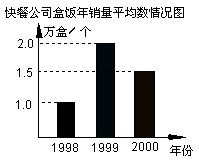
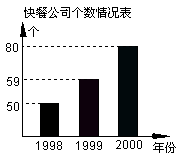
(1)1999年该地区销售盒饭共 万盒;
(2)该地区盒饭销量最大的年份是 ,这一年的年销量是 万盒。
(3)这三年中该地区每年平均销售盒饭多少万盒?
24、(本题8分)如图,E、F是□ABCD的对角线AC上两点,AE=CF.
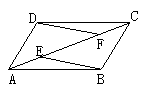 求证:(1)△ABE≌△CDF. (2)BE∥DF.
求证:(1)△ABE≌△CDF. (2)BE∥DF.
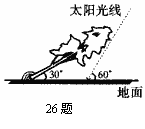 25、(本题8分)如图,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大 树在地面上的影长约为10m,求大树的长(保留两个有效数字,下列数据供选用:
25、(本题8分)如图,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大 树在地面上的影长约为10m,求大树的长(保留两个有效数字,下列数据供选用:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).
26、(本题10分)甲乙两人两次同时在同一粮店购买粮食(假设两次购买粮食的单价不相同),甲每次购买粮食100千克,乙每次购粮用去100元。
(1)假设![]() 、
、![]() 分别表示两次购粮的单价(单位:元/千克)。试用含
分别表示两次购粮的单价(单位:元/千克)。试用含![]() 、
、![]() 的代数式表示:甲两次购买粮食共需付款
元;乙两次共购买
千克的粮食;若甲两次购粮的平均单价为每千克
的代数式表示:甲两次购买粮食共需付款
元;乙两次共购买
千克的粮食;若甲两次购粮的平均单价为每千克![]() 元,乙两次购粮的平均单价为每千克
元,乙两次购粮的平均单价为每千克![]() 元,则
元,则![]() =
;
=
;![]() =
。
=
。
(2)规定:谁两次购粮的平均单价低,谁的购粮方式就更合算,请你判断甲乙两人的购粮方式哪一个更合算些?并说明理由。
27、(本题10分) 如图,某校广场有一段25米长的旧围栏,现打算利用该围栏的一部分(或全部)为一边,围成一块100平方米的长方形草坪(如图CDEF,CD<CF)已知整修旧围栏的价格是每米1.75元,建新围栏的价格是每米4.5元。
(1)若计划修建费为150元,能否完成该草坪围栏修造任务?
 (2)若计划修建费为120元,能否完成该草坪围栏修建任务?若能完成,请算出利用旧围栏多少米;若不能完成,请说明理由。
(2)若计划修建费为120元,能否完成该草坪围栏修建任务?若能完成,请算出利用旧围栏多少米;若不能完成,请说明理由。
28、(本题10分)如图所示:AB是⊙O的直径,BC是⊙为O的弦,⊙O的割线PDE垂直AB于点F,交BC于点G,∠BAC=∠BCP,求解下列问题:
(1)求证:PC是⊙O的切线;
(2)当∠ABC=30º、BG=![]() 、CG=
、CG=![]() 时,求以PD、PE的长为根的一元二次方程;
时,求以PD、PE的长为根的一元二次方程;
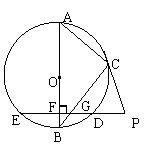 (3)当点C在劣弧上运动时,应具备什么条件可使结论BG2=BF•BO成立,试写出你的猜想,并说明理由。
(3)当点C在劣弧上运动时,应具备什么条件可使结论BG2=BF•BO成立,试写出你的猜想,并说明理由。
29、(本题12分)如图,抛物线![]() ,其中
,其中![]() 、
、![]() 、
、![]() 分别是△ABC的∠A、∠B、∠C的对边。
分别是△ABC的∠A、∠B、∠C的对边。
(1)求证:该抛物线与![]() 轴必有两个交点;
轴必有两个交点;
(2)设有直线![]() 与抛物线交于点E、F,与
与抛物线交于点E、F,与![]() 轴交于点M,抛物线与
轴交于点M,抛物线与![]() 轴交于点N,若抛物线的对称轴为
轴交于点N,若抛物线的对称轴为![]() ,△MNE与△MNF的面积之比为5∶1,求证:△ABC是等边三角形;
,△MNE与△MNF的面积之比为5∶1,求证:△ABC是等边三角形;
(3)在(2)的条件下,当![]() 时,设抛物线与
时,设抛物线与![]() 轴交于点P、Q,问是否存在过P、Q两点且与
轴交于点P、Q,问是否存在过P、Q两点且与![]() 轴相切的圆?若存在这样的圆,求出圆心的坐标;若不存在,请说明理由。
轴相切的圆?若存在这样的圆,求出圆心的坐标;若不存在,请说明理由。

30、(本题11分)设![]() 为正整数,且
为正整数,且![]() ,如果对一切实数
,如果对一切实数![]() ,二次函数
,二次函数![]() 的图象与
的图象与![]() 轴的两个交点间的距离不小于
轴的两个交点间的距离不小于![]() ,求
,求![]() 的值.
的值.