初中毕业、升学考试数学试题
(满分:150分 考试时间:120分钟)
一、填空题(每小题3分,计36分)
1.![]() 的相反数是 .
的相反数是 .
2.因式分解:![]() .
.
3.从《闽西日报》获悉:今年我市对农村九年制义务教育免除学杂费的中、小学生数约330000人.330000用科学记数法表示为 .
 4.不等式组
4.不等式组![]() 的解集是 .
的解集是 .
5.函数![]() 中自变量
中自变量![]() 的取值范围是 .
的取值范围是 .
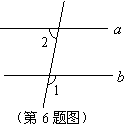
 6.如图,已知
6.如图,已知![]() ,则
,则![]() .
.
7.化简:![]() .
.
8.如图,小明在操场上距离旗杆18米的![]() 处,用测角仪测得旗杆
处,用测角仪测得旗杆![]() 的顶端
的顶端![]() 的仰角为
的仰角为![]() ,已知测角仪
,已知测角仪![]() 的高为1.4米,那么旗杆
的高为1.4米,那么旗杆![]() 的高为 米.(保留三个有效数字)
的高为 米.(保留三个有效数字)
9.圆锥的侧面展开图的面积为![]() ,母线长为3,则该圆锥的底面半径为 .
,母线长为3,则该圆锥的底面半径为 .
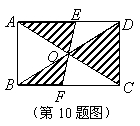
10.如图,矩形![]() 的对角线
的对角线![]() 和
和![]() 相交于点
相交于点![]() ,过点
,过点![]() 的直线分别交
的直线分别交![]() 和
和![]() 于点
于点![]() ,
,![]() ,则图中阴影部分的面积为 .
,则图中阴影部分的面积为 .
 | |||
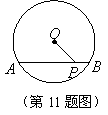 | |||
11.如图,已知![]() 的半径为5,弦
的半径为5,弦![]() 是弦
是弦![]() 上一点,且
上一点,且![]() ,则
,则![]() .
.
12.已知实数![]() 满足:
满足:![]() ,那么
,那么![]() 的值为 .
的值为 .
二、选择题(每小题4分,计32分)在每小题给出的四个选项中,只有一个是符合题目要求的,请把正确选项的代号填入题后的括号内
13.下列计算正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
14.下面四张扑克牌中,属于中心对称图形的是( )
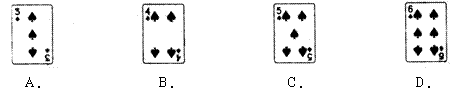 |
15.用换元法解分式方程![]() 时,设
时,设![]() ,则原方程可化为整式方程( )
,则原方程可化为整式方程( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
16.已知两圆的半径分别为3cm和7cm,圆心距为10cm,则这两圆的公切线条数是( )
A.1条 B.2条 C.3条 D.4条
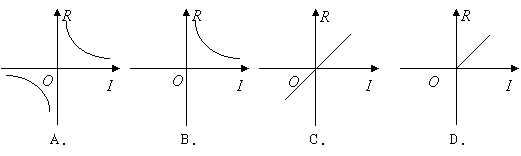 17.根据欧姆定律
17.根据欧姆定律![]() ,当电压
,当电压![]() 一定时,电阻
一定时,电阻![]() 与电流
与电流![]() 的函数图象大致是( )
的函数图象大致是( )
18.下列说法错误的是( )
A.矩形的四个角都相等 B.四条边都相等的四边形是菱形
C.等腰梯形的对角线相等 D.对角线互相垂直平分的四边形是正方形
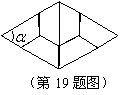 19.如图,小亮用六块形状、大小完全相同的等腰梯形拼成一个四边形,则图中
19.如图,小亮用六块形状、大小完全相同的等腰梯形拼成一个四边形,则图中![]() 的度数是( )
的度数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
20.已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,则线段
两点,则线段![]() 的长度为( )
的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
三、解答题(共8小题,计82分)
21.(8分)计算:![]()
 22.(8分)如图,在
22.(8分)如图,在![]() 中,点
中,点![]() 分别在
分别在![]() 上,在不添加辅助线的情况下,请你添加一个适当的条件,使
上,在不添加辅助线的情况下,请你添加一个适当的条件,使![]() 和
和![]() 全等,你添加的条件是 ,并给出你的证明.
全等,你添加的条件是 ,并给出你的证明.
证明:
 23.(9分)我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如下图),此图揭示了
23.(9分)我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如下图),此图揭示了![]() (
(![]() 为非负整数)展开式的项数及各项系数的有关规律.
为非负整数)展开式的项数及各项系数的有关规律.
例如:
![]() ,它只有一项,系数为1;
,它只有一项,系数为1;
![]() ,它有两项,系数分别为1,1,系数和为2;
,它有两项,系数分别为1,1,系数和为2;
![]() ,它有三项,系数分别为1,2,1,系数和为4;
,它有三项,系数分别为1,2,1,系数和为4;
![]() ,它有四项,系数分别为1,3,3,1,系数和为8;
,它有四项,系数分别为1,3,3,1,系数和为8;
……
根据以上规律,解答下列问题:
(1)![]() 展开式共有 项,系数分别为 ;
展开式共有 项,系数分别为 ;
(2)![]() 展开式共有 项,系数和为 .
展开式共有 项,系数和为 .
24.(10分)某县为了解初三6000名学生初中毕业考试数学成绩(分数为整数)从中抽取了200名学生的数学成绩进行分析,下面是200名学生数学成绩的频率分布表:
| 分组 | 频数 | 频率 |
| 89.5~99.5 | 12 |
|
| 99.5~109.5 | 24 | 0.12 |
| 109.5~119.5 | 36 | 0.18 |
| 119.5~129.5 | 68 | 0.34 |
| 129.5~139.5 |
| 0.2 |
| 139.5~149.5 | 20 | 0.1 |
| 合计 | 200 | 1 |
根据所给信息回答下列问题:
(1)频率分布表中的数据![]() ;
;
(2)中位数落在 分数段内;
(3)若成绩不低于120分的为优秀,试估计该县初三学生初中毕业考试数学成绩优秀的学生有 人.
25.(10分)已知:关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)求证:不论![]() 取何值,方程总有两个不相等的实数根;
取何值,方程总有两个不相等的实数根;
(2)若方程的两个实数根![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
26.(11分)某水果经销商上月份销售一种新上市的水果,平均售价为10元/千克,月销售量为1000千克.经市场调查,若将该种水果价格调低至![]() 元/千克,则本月份销售量
元/千克,则本月份销售量![]() (千克)与
(千克)与![]() (元/千克)之间满足一次函数关系
(元/千克)之间满足一次函数关系![]() .且当
.且当![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)已知该种水果上月份的成本价为5元/千克,本月份的成本价为4元/千克,要使本月份销售该种水果所获利润比上月份增加![]() ,同时又要让顾客得到实惠,那么该种水果价格每千克应调低至多少元?[利润=售价-成本价]
,同时又要让顾客得到实惠,那么该种水果价格每千克应调低至多少元?[利润=售价-成本价]
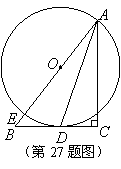 27.(12分)如图,已知点
27.(12分)如图,已知点![]() 为
为![]() 斜边
斜边![]() 上一点,以
上一点,以![]() 为圆心,
为圆心,![]() 为半径的圆与
为半径的圆与![]() 相切于点
相切于点![]() ,与
,与![]() 相交于点
相交于点![]() .
.
(1)试判断![]() 是否平分
是否平分![]() ?并说明理由;
?并说明理由;
(2)若![]() ,求
,求![]() 的半径.
的半径.
28.(14分)如图,已知抛物线![]() 与坐标轴交于
与坐标轴交于![]() 三点,点
三点,点![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点,
上的一个动点,![]() 于点
于点![]() .若
.若![]() ,且
,且![]() .
.
(1)确定![]() 的值:
的值:![]() ;
;
(2)写出点![]() 的坐标(其中
的坐标(其中![]() 用含
用含![]() 的式子表示):
的式子表示):
![]() ;
;
 (3)依点
(3)依点![]() 的变化,是否存在
的变化,是否存在![]() 的值,使
的值,使![]() 为等腰三角形?若存在,求出所有
为等腰三角形?若存在,求出所有![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
初中毕业、升学考试
参考答案及评分标准
数 学
一、填空题(每小题3分,共36分)
1.![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() 5.
5.![]()
6.![]() 7.
7.![]() 8.
8.![]() 9.
9.![]() 10.
10.![]() 11.
11.![]() 12.
12.![]()
二、选择题(每小题4分,共32分)
13.D 14.B 15.D 16.C 17.B 18.D 19.A 20.D
三、解答题(8小题,共82分)
21.(8分)
解:原式![]() ·································································· (5分)
·································································· (5分)
![]() ······························································································ (7分)
······························································································ (7分)
![]() ··································································································· (8分)
··································································································· (8分)
(备注:第一步每个计算对均给1分,第二步![]() 对1分,
对1分,![]() 对1分)
对1分)
22.(8分)
解:条件![]() (答案不唯一) ································································ (3分)
(答案不唯一) ································································ (3分)
证明:![]() 四边形
四边形![]() 是平行四形
是平行四形
![]()
![]() ································································· (6分)
································································· (6分)
又![]() ····················································································· (7分)
····················································································· (7分)
![]() ············································································· (8分)
············································································· (8分)
(备注:给出的条件只要能证明结论就给3分)
23.(9分)
解:(1)![]() ······································································································ (2分)
······································································································ (2分)
1,4,6,4,1 ·················································································· (4分)
(2)![]() ································································································· (6分)
································································································· (6分)
![]() ···································································································· (9分)
···································································································· (9分)
24.(10分)
解:(1)![]() ,
,![]() ························································································ (4分)
························································································ (4分)
(2)![]() ~
~![]() ·················································································· (7分)
·················································································· (7分)
(3)![]() ······························································································ (10分)
······························································································ (10分)
(备注:第1小题每空2分)
25.(10分)
解:(1)![]() ····················································· (2分)
····················································· (2分)
![]()
![]() ························································································· (3分)
························································································· (3分)
![]() 不论
不论![]() 取何值,方程总有两个不相等实数根 ············································· (4分)
取何值,方程总有两个不相等实数根 ············································· (4分)
(2)解法一:由原方程可得![]()
或![]() ················································· (6分)
················································· (6分)
![]() ··························································· (7分)
··························································· (7分)
又![]()
![]() ······················································· (8分)
······················································· (8分)
![]() ····················································································· (9分)
····················································································· (9分)
经检验:![]() 符合题意.
符合题意.
![]() 的值为
的值为![]() . ········································································ (10分)
. ········································································ (10分)
解法二:根据根与系数关系有![]() ········· (5分)
········· (5分)
又![]() ················································· (6分)
················································· (6分)
![]() ·························································· (7分)
·························································· (7分)
整理得![]() ············································································ (8分)
············································································ (8分)
解得![]() ································································ (9分)
································································ (9分)
经检验![]() 是增根舍去
是增根舍去
![]() 的值为
的值为![]() . ········································································ (10分)
. ········································································ (10分)
26.(11分)
解:(1)由已知得![]() ··························································· (3分)
··························································· (3分)
解得![]() ······································································· (5分)
······································································· (5分)
![]()
(2)由题意可得
![]() ······················ (8分)
······················ (8分)
整理得![]() ···························································· (9分)
···························································· (9分)
得![]() (舍去) ························································ (10分)
(舍去) ························································ (10分)
答:该种水果价格每千克应调低至![]() 元. ········································· (11分)
元. ········································· (11分)
27.(12分)
(1)判断:![]() 平分
平分![]() . ······································································ (2分)
. ······································································ (2分)
证法一:连结![]()
![]() 切
切![]() 于
于![]()
![]() ·············································································· (3分)
·············································································· (3分)
又![]() 为
为![]() ,且
,且![]()
![]()
![]()
![]() ················································································ (4分)
················································································ (4分)
又![]()
![]() ··············································································· (5分)
··············································································· (5分)
![]() ················································································ (6分)
················································································ (6分)
 证法二:连结
证法二:连结![]()
![]() 是
是![]() 直径
直径
![]()
![]() ······························· (3分)
······························· (3分)
又![]()
![]() ································································· (4分)
································································· (4分)
又![]() ······························································· (5分)
······························································· (5分)
![]() ················································································ (6分)
················································································ (6分)
证法三:连结![]()
![]() 是
是![]() 直径
直径
![]() ·········································································· (3分)
·········································································· (3分)
又![]()
![]()
![]()
![]() ··············································································· (4分)
··············································································· (4分)
又![]() ·························································· (5分)
·························································· (5分)
![]() ················································································ (6分)
················································································ (6分)
(2)解法一:设![]() ,则
,则![]() ········································ (7分)
········································ (7分)
据切割线定理得![]() ······································· (8分)
······································· (8分)
得![]() ··········································· (9分)
··········································· (9分)
又![]()
![]() ································································· (10分)
································································· (10分)
![]()
![]() ········································································· (11分)
········································································· (11分)
![]() 的半径为
的半径为![]() ··························································· (12分)
··························································· (12分)
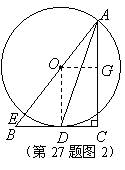 解法二:如图2,过
解法二:如图2,过![]() 作
作![]() ,又
,又![]() ,
,
则四边形![]() 为矩形.
为矩形.
![]()
又![]()
![]() ·································· (10分)
·································· (10分)
![]()
![]() (舍去) ······················································ (11分)
(舍去) ······················································ (11分)
![]() 的半径为
的半径为![]() ·································································· (12分)
·································································· (12分)
备注:本解法是在解法一得![]() 的基础上进行的.
的基础上进行的.
解法三:如图(1)![]()
![]() ·········································································· (7分)
·········································································· (7分)
又![]()
![]() ············································································· (8分)
············································································· (8分)
又![]()
![]()
![]() ··································································· (9分)
··································································· (9分)
又![]() ,则
,则![]() ························································· (10分)
························································· (10分)
在![]() 中,
中,![]() 得
得![]()
在![]() 中,
中,![]() ·························· (11分)
·························· (11分)
![]() 的半径的长
的半径的长![]() ··········································· (12分)
··········································· (12分)
(备注:本大题第2小题解法较多,若出现其它解法,请根据评分标准量分)
28.(14分)
解:(1)![]() ······························································································· (2分)
······························································································· (2分)
![]() ································································································ (4分)
································································································ (4分)
(2)![]() ····························································································· (5分)
····························································································· (5分)
![]() ···························································································· (6分)
···························································································· (6分)
![]() ······················································································ (8分)
······················································································ (8分)
(3)存在![]() 的值,有以下三种情况
的值,有以下三种情况
①当![]() 时
时
![]() ,则
,则![]()
![]()
![]() ························································································ (10分)
························································································ (10分)
②当![]() 时
时
得![]()
![]() ························································································ (12分)
························································································ (12分)
③当![]() 时,如图
时,如图
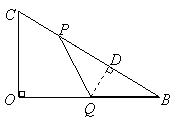 解法一:过
解法一:过![]() 作
作![]() ,又
,又![]()
则![]()
又![]()
![]()

![]() ········································································ (14分)
········································································ (14分)
解法二:作![]() 斜边中线
斜边中线![]()
则![]() ,
,
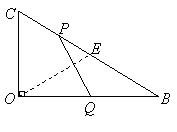 此时
此时![]()
![]()
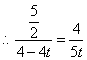
![]() ···································································· (14分)
···································································· (14分)
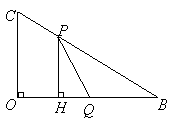 解法三:在
解法三:在![]() 中有
中有![]()
![]()
![]()
![]() (舍去) ··········································· (14分)
(舍去) ··········································· (14分)
又![]()
![]() 当
当![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.