初中数学毕业考试试卷（新课标华师大版）
一、填空题(本题共9个小题，每小题3分，满分27分)
1. －2006的相反数是____________。
2．已知函数y＝－2x+3，当x＝—1时，y＝____________。
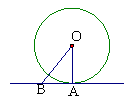
3．如图，已知直线AB是⊙O的切线，A为切点，∠OBA=52°，
则∠AOB=_____°
4. 方程＝的解是____________。
5．众所周知，几何图形中有许多轴对称图形，写出一个你最喜欢的轴对称图形是______。
6. 从、、、4中随机抽取一个根式与是同类二次根式的概率是__________。
| 张宇 | 李明 | |
| 笔试 | 78 | 92 |
| 试教 | 94 | 80 |
7．某学校决定招聘一位数学教师，对应聘者进行笔试和试教
两项综合考核，根据重要性，笔试成绩占30％，试教成绩占
70％．应聘者张宇、李明两人的得分如右表：
如果你是校长，你会录用____________。
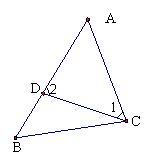
8．如图，要使△ACD∽△ABC，只需添加条件____________。
(只要写出一种合适的条件即可)．
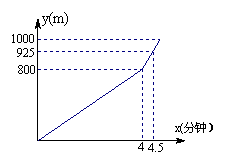9．2006年5月29日—6月1日，“国际龙舟节”在岳阳汩罗江举行．某龙舟队在1000米比赛项目中，路程y(米)与时间x(分钟)之间的函数图象如图所示．根据图中提供的信息，该龙舟队的比赛成绩是____________分钟．
 |
二、选择题（3′×9＝27′）
10、计算：（－2）3的值是________。
A：－6 B：6 C：－8 D：－9
11、三峡电站是目前世界上最大的电厂，装机总容量为1820万kw，这个数用科学记数法表示为__________kw。
A：0.182×108 B：1.82×107 C：1.82×106 D：1820×104
12、下列图形中，不是正方体的表面展开图的是___________。
A： B： C： D：
13、下列说法正确的是_________。
A：近似数0.203有两个有效数字 B：15的算术平方根比4大
C：多项式a－ab分解因式是a(1－b) D：函数y＝－的图像在第一、三象限。
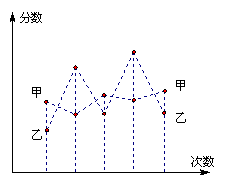14、右图是甲、乙两位同学的5次数学考试的成绩
的折线统计图，你认为成绩较稳定的是_________
A：甲 B：乙
C：甲、乙的成绩一样稳定 D：无法确定
15、钟面上的分针长为6cm，经过25分钟时间，分针在
钟面上扫过的面积为____________cm2
A：π B：15π C：9π D：30π
16、不等式3(x－1)+4≥2x的解集在数轴上表示为______。
A： B： C： D：
17、如图，在△ABC中，AB=AC，∠A＝30°，DE垂直平分AC，则∠BCD的度数为____。
A：80° B：75° C：65° D：45°
18、小明从右边的二次函数y＝ax2+bx+c图像中，观察得出了下面的五条信息：①a＜0
②c＝0 ③函数的最小值为－3 ④当x＜0时，y＞0 ⑤当0＜x1＜x2＜2时，y1＞y2。
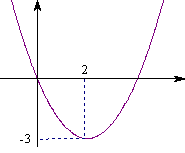你认为其中正确的有______个。
A：2 B：3
C：4 D：5
三、解答题（66′）
19、先化简，再求值： (2a－b)2－2a(a－b)－(2a2＋b2)，其中a＝+1, b＝－1
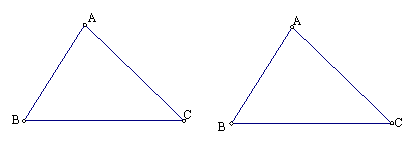
20、某农场有一块三角形土地，准备分成面积相等的4块，分别承包给4位农户，请你设计两种不同的分配方案(在已给的图形中直接画图，保留画图痕迹，不写画法)
| 捐款 | 1 | 2 | 5 | 10 |
| 人数 | 6 | 7 |
21、今年5月27日，印尼中爪哇省发生强烈地震，给当地人民造成巨大的经济损失．某学校积极组织捐款支援灾区，初三(1)班55名同学共捐款274元，捐款情况如右表．表中捐款2元和5元的人数不小心被墨水污染已看不清楚，请你帮助确定表中数据，并说明理由．
22、 如图△ADF和△BCE中，∠A=∠B，点D、E、F、C在同—直线上，有如下三个关系式：① AD=BC；② DE=CF；③BE∥AF。
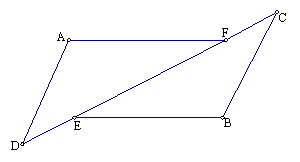1)请用其中两个关系式作为条件，另一个作为结论，写出所有你认为正确的命题．(用序号写出命题书写形式，如：如果╳、╳，那么╳)
2)选择(1)中你写出的—个命题，说明它正确的理由．
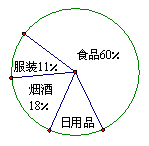23、2006年“五一”黄金周心连心集团湖南岳阳超市，七天销售总额达120万元，具体分配情况如图．
1)由图可知，日用品类销售额占总销售额的百分比
为_______，日用品类销售额是______万元．
2)已知2005年心连心超市在“五一”黄金周的食品类
销售额是60万元，若年增长率保持不变，请预测2007
年“五一”黄周食品类销售额是多少万元？
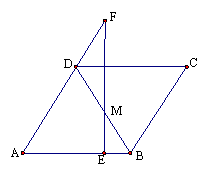24、如图，在菱形ABCD中，∠A=60°，AB=4，E是边AB上一动点，过点E作EF⊥AB交AD的延长线于点F，交BD于点M．
(1)请判断△DMF的形状，并说明理由．
(2)设EB=x，△DMF的面积为y，求y与x之间
的函数关系式．并写出x的取值范围．
| 胜一场 | 平一场 | 负一场 | |
| 积分 | 3 | 1 | 0 |
| 奖金（元/人） | 2000 | 1000 | 0 |
25为了迎接2006年德国世界杯足球赛的到来，某足球协会举办了一次足球联赛，其记分规则及奖励方案如下表：
当比赛进行到14轮结束（每队均需比赛14场）时，甲队共积分25分。
① 请你通过计算，判断甲队胜、平、负的场数？
② 若每场比赛，每名参赛队员均可获得800元的出场费，设甲队中一名参赛队员所得的奖金与出场费的和为W元，试求W的最大值？
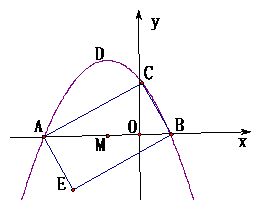
26、如图抛物线y＝
，x轴于A、B两点，交y轴于点c，顶点为D。
1）求A、B、C的坐标。
2）把△ABC绕AB的中点M旋转180°，得到四边形AEBC：
①求E点坐标。
②试判断四边形AEBC的形状，并说明理由。
3）试探索：在直线BC上是否存在一点P，使得△PAD的周长最小，若存在，请求出P点的坐标；若不存在，请说明理由？
 |