初三第二阶段考试数学试卷
一、选择题（3分×8=24分）
1．已知x=1是一元二次方程
的一个根，则m的值是：
A．1 B．0 C．0或1 D．0或－1
2．下列命题错误的是：
A．平行四边形的对角相等 B．等腰梯形的对角线相等
C．两条对角线相等的平行四边形是矩形
D．对角线互相垂直的四边形是菱形
3．若分式
的值为零，则x的值为：
A．1 B．2 C．1或2 D．－1或－2
4．将方程
的左边配成一个完全平方式正确的是：
A．
B．
C．
D．
5．如图，△ABC中，AB=AC，点D在AC上，且BD=BC=AD，则∠A的度数为：
A．30° B．45° C．36° D．72°
6．已知点A（－3，y1），B（－2，y2），C（1，y3）都在反比例函数
的图象上，则：
A．y1 ＜y2 ＜y3 B．y3 ＜y2 ＜y1 C．y2 ＜y1＜ y3 D．y3 ＜y1 ＜y2
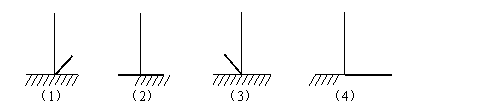7．下面四幅图是小刚一天之中在学校观察到的旗杆的影子，将它们按时间先后顺序进行排列应是：
A．（1）（2）（3）（4）
B．（2）（3）（1）（4）
C．（2）（1）（3）（4）
D．（3）（4）（1）（2）
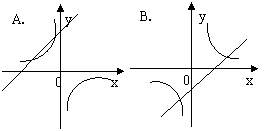
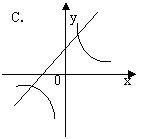
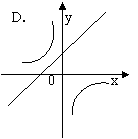
8．已知关于
的函数
与
，它们在同一坐标系内的图象大致是：
 |  |  | |||
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答 案 |
|
|
|
|
|
|
|
|
二、填空题（3分×8=24分）
9．把方程
化成一元二次方程的一般形式为
，其二次项系数为
。
10．请写出一个二次项系数为1，两实根之和为3的一般形式的一元二次方程为 。
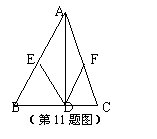
11．如图，在△ABC中，AD⊥BC，垂足为D，E、F分别是AB、AC的中点，连结DE、DF，△
ABC满足 时，四边形AEDF是菱形（填写一个你认为恰当的条件即可）。
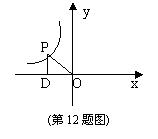
12．如图，点P是反比例函数
上一点，PD⊥x轴于点D，且S△POD的面积为1，则反比例函数的解析式为
。
13．等腰三角形中有一个角为30°，则这个三角形的顶角为 。
14．某商场四月份的营业额为a万元，五月份的营业额为1.2a万元，如果按照相同的月增长率计算，该商场六月份的营业额为 万元。
15．在相同的时刻物高与影长成比例，如果一电杆在地面上的影长为50米，同时高为1米的测杆的影长为2米，那么电杆的高为 。
16．如图，矩形AOCB的两边OC、OA分别位于x轴、y轴上，点B的坐标为B（
，5），
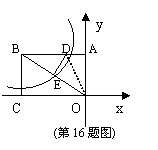
D是AB边上的一点，将△ADO沿直线OD翻折，使A点恰好落在对角线OB上的点E处，若点E在一反比例函数的图象上，那么该函数的解析式为
。
三、解答题（本题共8小题，满分72分）
17．解方程（8分）
（1）
（2）
18．（本题满分6分）请画出这个几何体的三视图。
 |
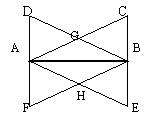19．（本题满分9分）如图，在Rt△ABC与Rt△ABD中，∠ABC=∠BAD=90°，AD=BC，AC、BD相交于点G，过点A作AE∥DB交CB的延长线于点E，过点B作BF∥CA交DA的延长线于点F，AE、BF相交于点H。（1）图中有若干对三角形是全等的，请你任选一对进行证明。（不添加任何辅助线）（2）证明四边形AHBG是菱形。（3）若使四边形AHBG是正方形，还需在Rt△ABC的边长之间再添加一个什么条件？请你写出这个条件（不必证明）。
20．（本题满分9分）某旅社有100张床位，若每床每夜收租金10元时，客房可以全部租出；若每床每晚每高出2元，便减少10张床租出，若旅社计划每夜租金为1120元，从节约成本去考虑，每床每夜租金是多少元？
21．（本题满分9分）一条东西走向的高速公路上有两个加油站A、B，在A的北偏东45°方向还有一个加油站C，C到高速公路的最短距离是30km，B、C之间的距离是60km，想要经过C修一条笔直的公路与高速公路相交，使两条交叉口P到B、C的距离相等，请求出交叉口P与加油站A的距离（结果可保留根号）。
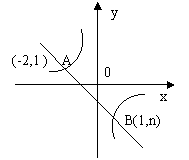
22．（本题满分9分）如图，一次函数
的图象与反比例函数
的图象交于A、B两点。（1）利用图中条件，求反比例函数和一次函数的表达式；
（2）根据图象写出使一次函数的值大于反比例函数值的x的取值范围。
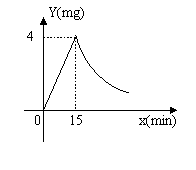
23．（本题满分10分）按国家粮食储备库规定，粮食进仓之前，都要对粮仓进行药熏消毒，已知药物燃烧时，仓内每立方米空气中的含药量y(mg)与时间x(min)成正比例，药物烧完后，y与x成反比例，如图，现测得15分钟烧完，此时仓内空气中每立方米的含药量为4mg，请根据提供的信息回答问题：
（1）药物燃烧时，y与x的关系式是 ，燃烧完后的关系式是 。
（2）研究表明，当空气中每立方米的含药量不低于2mg且持续时间不少于35分钟时，消毒才为彻底，那么此次消毒是否符合要求，请通过计算回答。
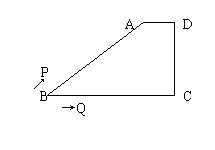
24．（本题满分12分）如图，在梯形ABCD中，AB=BC=10cm，CD=6cm，∠C=∠D=90°。
（1）求AD。（2）动点P、Q分别以3cm/s、2cm/s的速度同时从B点出发，点P沿BA、AD运动到点D停止，点Q随之停止运动，设P、Q同时从点B出发时间为t(s)时，△PBQ的面积为y(cm2)，求y与t之间的函数关系式，并写出自变量的取值范围。
（3）点P、Q在（2）的运动过程中，△PBQ的面积有最大值吗？如果有请求出这个最大值，并求t的值；如果没有请，说明理由。