初三年级数学第四次月考试卷

初三年级数学第四次月考试卷

（满分150分，考试时间90分钟）　

考生注意：填空题、选择题的答案写在解答题的卷面上，此页试卷不用上交．

一、填空题（每小题3分，共36分）

1．分解因式： 　　　　　　　　　　　．

2．．方程的根是　　　　 　　　　　．

3． 方程的根是　　　　 　　　　　．

4．如图，ΔABC的中线AD、BE相交于点F，则=　　　　．

5．在RtΔACB中， ∠C=90⁰， ∠A=30⁰，点D（与点A不重合）在边AC上，且AD<CD，若经过点D的直线截ΔACB所得的三角形与ΔACB相似，则这样的直线共有　　 条．

6．在如图的山坡上植树，已知坡比，要使株距（相邻两树间的水平距离）为4米，则斜坡上相邻两棵树之间的坡面距离是　　　　　 米．

　　 第4题图　　 　　　第6题图　　　　　　  第8题图　　　　　　 第10题图

7．如果等腰三角形中的两条边长分别是2和5，那么底角的余弦为　　　　．

8．如图，⊙O的半径OC=5厘米，直线m⊥OC，垂足为H，且m交⊙O 于A、B两点，AB=8厘米，则m沿OC所在直线向下平移_______厘米可与⊙O相切．

9．已知△ABC的周长为20，△ABC的内切圆与边AB相切于点D，AD=4，那么BC=　　　　 ．

10．如图，△ABC是直径为10 cm的⊙O的内接等腰三角形，如果此等腰三角形的底边

BC=8 cm，那么△ABC的面积为　　　　　　 cm²．

11．如果两圆的半径分别为1和2,圆心距为3,那么它们的一条外公切线长是__________．

12．在矩形ABCD中，AB=5，BC=12，⊙A的半径为2，若以C为圆心作一个圆，使⊙C与⊙A相切，那么⊙C的半径为　　　　　　  ．

二、选择题（每小题4分，共16分）

13．已知AE、CF是锐角△ABC的两条高，如果AE∶CF=3∶2，则sinA∶sinC等于（　　　）．

　 （A）3∶2 ；　　 　　　　　　　（B）2∶3　；　

（C）9∶4 ；　　　　　　　　　 （D）4∶9 ．

14．已知A、B两点，如果A对B的俯角为α，那么B对A的仰角为（　　　 ）．

(A) α； 　　　　　　　　　　　 (B)90°-α； 　　

(C) 90°+α； 　　　　　　　　　 (D) 180°-α．

15．下列命题中，正确的是（　　 ）．

（A）三角形的外心一定在三角形的外面；　

（B）相交两圆的连心线垂直平分两圆的公共弦；

（C）三角形的重心到三角形三个顶点的距离相等；

（D）两圆相切时公切线必有三条．

16．已知⊙和⊙的半径分别为4和，圆心距＝5，则⊙与⊙

的公切线的条数为(　　　) ．

（A）1条；　　　　　　　  （B）2条；　　　　

（C）3条 ；　　　　　　　 （D） 4条．

初三年级数学第四次月考试卷

（满分150分，考试时间90分钟）　 2006年12月28日

一、填空题答案：

1．________________；　　2．________________；　　3．________________；

4．________________； 　 5．________________；　　6．________________；

7．________________；　　8．________________；　　9．________________；

10．________________；　11．________________；　 12．________________．

二、选择题答案：13．　　　14．　　　 15．　　　　16．

三、简答题（第17~18题每题9分，第19~21题每题10分，共48分）

17．　计算：

18． 如图，△ABC中，∠C=90⁰，点D在BC上，BD=4， AD=BC，．

求：（1）DC的长；　 （2）的值．

19．如图，一拦水坝的横断面积是梯形，坝的上底CD的宽为6米，坡角∠DAB=30⁰，另一斜坡BC的坡度为，坝高为10米，求坝底宽AB的长．

20． 机车行驶24千米后，因故受阻12分钟，以后再以每小时比原来快6千米的速度驶往目的地，虽然后一段路程比前一段路程长12千米，但仍准时到达．求机车原来的速度．

21．如图，已知点C为⊙O的直径AB延长线上的一点，将线段AC绕点C顺时针旋转30⁰至CD，恰好CD与⊙O相切于点P，连结AD交⊙于点E，求AE∶ED的值．

四、解答题（第22~24题每题12分，第25题14分，共50分）

22．如图，△ABC中，∠ABC=90⁰，以AB为直径作⊙O交AC于点D，如果E为BC的中点，求证DE是⊙O的切线．

23．已知△ABC的三边长为6、8、10，⊙O的圆心在△ABC的边上且与其它两边相切，求⊙O的半径r ．

　　　　　 　　　　　　

　　　 备用图　　　　　　　　　  备用图　　　　　　　　　　　  备用图

24．如图，⊙O半径为1，点P在射线OA上．⊙P的半径为2，交⊙O于Q、R两点．设OP = x．

（1）写出x的取值范围_________________________；

（2）当x=时，∠QPR的度数为_________；

（3）当QR=1时，求PQ、QO、OR、RP围成的图形面积．

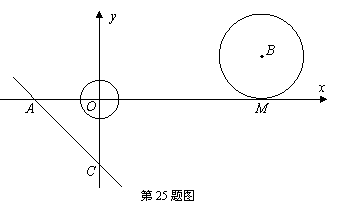
25．如图，在平面直角坐标系中，以坐标原点O为圆心的⊙O的半径为，直线l： 与坐标轴分别交于A、C两点，点B的坐标为(4，1)，⊙B与x轴相切于点M．

（1）求点A的坐标及∠CAO的度数；

（2）⊙B以每秒1各单位长度的速度沿x轴负方向平移，同时，直线l绕点A顺时针匀速旋转．当⊙B第一次与⊙O相切时，直线l也恰好与⊙B第一次相切．

①当⊙B第一次与⊙O相切时，求圆心B₁的坐标；

②当直线l恰好与⊙B第一次相切时，设切点为P，求∠PAO的度数；

③直线AC绕点A每秒旋转多少度？