初三年数学中考模拟试卷(五)

初三年数学中考模拟试卷(五)

班级:　　　　 　姓名:　　　　　　 　座号:　　　　

　一、选择题

　　1．－5的绝对值是（　）．

　　　A．5 　　 B．　　　 C．　　　D．－5　　　　　　　　　　　　　　　　　　　　　　　　　　

　　2．计算的结果是（　）．

　　　A．－9　  B．－6　　　C．　　　D．

　　3．计算的结果是（　）．

　　　A． 　　B．a　　　 C． 　　　 D．

　　4．2002年我国发现首个世界级大气田，储量达6000亿立方米，6000亿立方米用科学记数法表示为（　）亿立方米．

　　　A． 　B．　　C．　　D．

　　5．下列图形中，不是中心对称图形的是（　）．

　　　A．菱形 　　　 B．矩形 　　 C．正方形　　　 D．等边三角形

　　6．如果两圆的半径分别为3 cm和5 cm，圆心距为10 cm，那么这两个圆的公切线共有（　）．

　　　A．1条 　　　　B．2条　　  C．3条　　　　  D．4条

　　7．如果反比例函数的图象经过点P（－2，3），那么k的值是（　）．

　　　A．－6　　　　 B． 　　 C．　 　　　D．6

　　8．在△ABC中，∠C＝90°．如果 ，那么sinB的值等于（　）．

　　　A．　　　　 B．　　　 C． 　　　　 D．

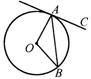
9．如图，CA为⊙O的切线，切点为A，点B在⊙O上．如果∠CAB＝55°，

那么∠AOB等于（　）．

　　　A．55° 　　　 B．90°　　　C．110° 　　　 D．120°

　　10．如果圆柱的底面半径为4 cm，母线长为5 cm，那么它的侧面积等于（　）．

　　　A．20p　 B．40p　　C．20 　　　D．40

中模(五)--1

　

11．若关于x的一元二次方程有两个不相等的实数根，则k的取值范围是（　）．

　　A．k＜1　　　　B．k≠0　　　 C．k＜1且k≠0 　　D．k＞1

12．在抗击“非典”时期的“课堂在线”学习活动中，李老师从5月8日至5月14日在网上答题个数的记录如下表：

日期	5月8日	5月9日	5月10日	5月11日	5月12日	5月13日	5月14日
答题个数	68	55	50	56	54	48	68

　　在李老师每天的答题个数所组成的这组数据中，众数和中位数依次是（　）．

　　A．68，55　　　　B．55，68　　　　C．68，57　　　　 D．55，57

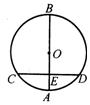
13．如图，AB是⊙O的直径，弦CD⊥AB，垂足为E．

若AB＝10，CD＝8，则AE的长为（　）．

　　A．2　 　　　　　B．3　　　　　　 C．4　　　　　　　D．5

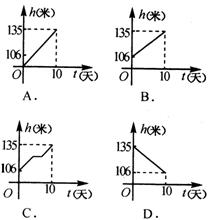14．三峡工程在6月1日至6月10日下闸蓄水期间，水库水位由106米升至135米，高峡平湖初现人间．假设水库水位匀速上升，那么下列图象中，能正确反映这10天水位h（米）随时间t（天）变化的是（　）．

二、填空题

15．在函数中，自变量x的取值范围是________．

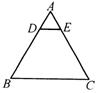
16．如图，在等边三角形ABC中，点D、E

分别在AB、AC边上，且DE∥BC．

如果BC＝8 cm，AD∶AB＝1∶4，

那么△ADE的周长等于________ cm．

17．如图，B、C是河岸边两点，A是对

岸岸边一点，测得∠ABC＝45°，∠ACB＝45°，

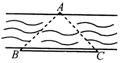BC＝60米，则点A到岸边BC的距离是________米．

18．观察下列顺序排列的等式：

　　9×0＋1＝1，

　　9×1＋2＝11，

　　9×2＋3＝21，

　　9×3＋4＝31，

　　9×4＋5＝41，

……　　猜想：第n个等式（n为正整数）应为________．

三、解答题

19．分解因式：．

　20．计算：

　

21．用换元法解方程

　22．如图，在□ABCD中，点E、F在对角线AC上，且AE＝CF．请你以F为一个端点，

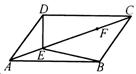和图中已标明字母的某一点连成一条新线段，猜想并证明它和图中已有的某一条线段相等（只须证明一组线段相等即可）．

　　（1）连结________．

　　（2）猜想：________＝________．

（3）证明：

中模(五)--2

　23．列方程或方程组解应用题：

　　在社会实践活动中，某校甲、乙、丙三位同学一同调查了高峰时段北京的二环路、三环路、四环路的车流量（每小时通过观测点的汽车车辆数），三位同学汇报高峰时段的车流量情况如下：

　　甲同学说：“二环路车流量为每小时10000辆．”

　　乙同学说：“四环路比三环路车流量每小时多2000辆．”

　　丙同学说：“三环路车流量的3倍与四环路车流量的差是二环路车流量的2倍．”

　　请你根据他们所提供的信息，求出高峰时段三环路、四环路的车流量各是多少．

24．已知：关于x的方程　　　　　　　　 的两个实数根是、，且

如果关于x的另一个方程　　　　　　　　　  的两个实数根都在和之间，求m的值．

25．已知：在ABC中，AD为∠BAC的平分线，以C为圆心，CD为半径的半圆交BC的延长线于点E，交AD于点F，交AE于点M，且∠B＝∠CAE，FE∶FD＝4∶3．

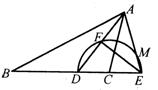（1）求证：AF＝DF；

　　（2）求∠AED的余弦值；

　　（3）如果BD＝10，求△ABC的面积．

	中模(五)--3

26．已知：抛物线与x轴的一个交点为A（－1，0）．

　（1）求抛物线与x轴的另一个交点B的坐标；

　（2）D是抛物线与y轴的交点，C是抛物线上的一点，且以AB为一底的梯形ABCD的面积

为9，求此抛物线的解析式；

　（3）E是第二象限内到x轴、y轴的距离的比为5∶2的点，如果点E在（2）中的抛物线上，且它与点A在此抛物线对称轴的同侧，问：在抛物线的对称轴上是否存在点P，使△APE的周长最小?若存在，求出点P的坐标；若不存在，请说明理由．