初三数学试卷
Ⅰ基础部分（80分）
一、 选择题（3＊8＝24分）
1. 下列方程没有实数根的是（ ）
A、x2－x－=0 B、
C、
D、
2. 为了解决百姓买药难的问题，国家决定对某种药品两年内降价19%，若平均每年降价的百分率为x，则列出的正确方程是( )
A、(1+x)2=1－19% B、2(1－x)=1－19%
C、2(1+x)=1－19% D、(1－x)2=1－19%
3. 某人沿倾斜角为β的斜坡前进n米时，他上升的最大高度为m米，则（ ）
A、m=n sinβ B、n=m sinβ C、m=n cosβ D、n=m cosβ
4. 下列命题：
①弧AB的度数与弧CD的度数相等，则弧AB所对的圆心角与弧CD所对的圆心角的度数相等。
②平分弦的直径垂直于弦。③垂直于半径的直线是圆的切线
④三角形的内心到三角形三个项点距离相等。其中正确的个数是（ ）
A、1 B、2 C、3 D、4
5. 已知，在正比例函数y=(2m－1)x的图象上有两点A（x1，y1）、B（x2，y1）当x1＜x2时，y1＞y2，那么m的取值范围是（ ）
A、
B、
C、m＜2 D、m＞2
6.
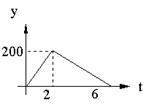
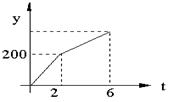
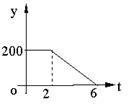某产品的生产流水线每小时可生产100件产品，生产前没有产品积压，生产2小时后，安排2人装箱，若每小时装产品150件，流水线继续生产。未装箱数量（y）是时间（t）的函数，那么这个函数图象大致是（ ）
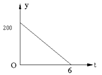
A B C D
7. 直线和圆相交，圆的半径为R，直线到圆心的距离为5，则（ ）
A、R＜5 B、R＞5 C、R＝5 D、R≥5
8. 过⊙O内点M的最长弦为10cm，最短弦长为8cm，则OM长为（ ）
A、5cm B、4cm C、3cm D、2cm
二、填空题
9.
△ABC中，∠C＝90。，sinA=
，则cosB=__________
10.
函数y=
的自变量取值范围是＿＿＿＿＿＿＿
11. 一次函数y=kx+b的图像经过一、二、四象限，则b＿＿，函数y随x的增大而＿＿＿＿＿＿
12.
Rt△ABC中，∠C＝90。，∠A＝30。，AB=10cm，以C为圆心8cm为半径作⊙C，则A点在⊙C＿＿＿，B点在⊙C＿＿＿
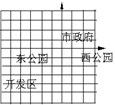
13. 某城市是棋盘是花园城市，每个小正方形边长为1个单位。现以市政府为坐标原点，建立直角坐标系，标出西公园、东公园的坐标。西公园＿＿＿＿＿，东公园＿＿＿＿
14. 关于x的一元二次方程4x2+mx－6=0的一根x1=3，则另一根x2=________m=________
15.
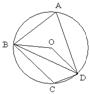△ABC中，∠A＝50。，∠B＝60。，O是△ABC的内心，则，∠BOC＝＿
16. 如图，四边形ABCD内接于⊙O，∠A∶∠C＝4∶5，
则∠OBD＝＿＿＿＿
17.
已知函数
的图象过点（－2,3），
则此图象与两坐标轴围成的图形的面积是＿＿＿＿
三、解答题（共29分）
18. 一个矩形长6cm，宽4cm，它的每边都减少xcm后，得新矩形的周长为ycm，写出y与x之间的函数关系式，并画出它的图象（9分）
19.
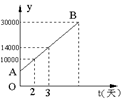（10分）某水库原有一定量储水，为备足水源，今从上游向水库注水，（注满30000m3为止），水库蓄水量y (m3）与注水时间t(天)成一次函数，其图象如所示。求：①蓄水量y(m3)与注水时间t(天)之间的函数关系式。②水库原有储水量多少m3 ③水库注满水需要多少天？
20.
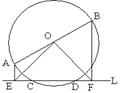(10分)如图，AB是⊙O的直径，直线L交⊙O于C、D，过A、B两点分别作直线L的垂线，垂足分别为E、F，连接OE、OF。①求证：CE＝DF，OE＝OF
②若AB＝10，CD＝8，求AE＋BF的长。
Ⅱ能力部分（20分）
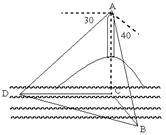
21. 如图，某小岛观察哨A，距水平面500米高（即AC＝500米），在小岛的正南方测得海上巡逻艇B的俯角为30。。现渔船D遇到险情，观察所命令巡逻艇必须在5分钟赶到救援，问巡逻艇的速度至少要达到多少？（使用计算器，结果精确到个位）（本题满分10分）
22.
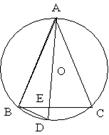如图，△ABC内接于圆，E为BC上任一点，AE的延长线交圆于D，连结BD。①当△ABC满足什么条件时，AB2＝AE·AD，并证明。②其余条件不变，当E为BC延长线上一点时，连结AE交圆于点在D，是否仍有AB2＝AE·AD成立？若成立，请画图并证明；若不成立，请说明理由。（10分）