初三数学周练2
班别： 姓名：
一、选择题：
1、在直角三角形、等腰三角形、矩形、角这四个图形中，是轴对称图形，但不是中心对称
图形的个数共有（ ）
A、1个 B、2个 C、3个 D、4个
2、在Rt△ABC中，∠C＝90O，a=30,b=40，则c的长为（ ）
A、30 B、40 C、50 D、60
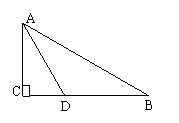
3、如图，在Rt△ABC中，∠C＝90O，∠A的平分线交BC于D，
CD=12cm，则点D到AB的距离为（ ）
A、6cm B、24cm C、12cm D、8cm
4、在△ABC中，∠B和∠C的角平分线相交于点O，∠A＝60O，则∠BOC的度数是（ ）
A、100O B、110O C、120O D、130O
5、以下列各组线段为边，能组成直角三角形的是（ ）
A、2cm,2cm,4cm B、7cm,6cm,3cm C、6cm,8cm,10cm D、5cm,5cm,6cm
6、下列条件中，不能使两个三角形全等的条件是（ ）
A、两边一角对应相等 B、两角一边对应相等
C、三边对应相等 D、两边和它们的夹角对应相等
7、在三角形内，且到三角形各边距离相等的点是（ ）
A、三边中线的交点 B、三个角平分线的交点
C、三条高的交点 D、三边垂直平分线的交点
8、在①
，②
，③
，④
中，一元二次方程共有（ ）。
A、1个 B、2个 C、3个 D、4个
9、一元二次方程
经过配方的结果是（ ）
A、
B、
C、
D、
10、若关于x的方程
是一元二次方程，则m的值为（ ）
A、m=2或m= -2 B、m=2 C、m= -2 D、m
2
11、方程
的根是（ ）
A、
B、
C、
D、原方程无解
12、已知菱形两条对角线的长分别是12cm和16cm，则它的边长是（ ）
A、6cm B、8cm C、10cm D、12cm
13、如图，在正方形ABCD中，延长BC至点E，使CE=AC，连接AE交CD于F，那么∠AFC的度数是（ ）
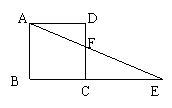A、112.5O B、125O C、135O D、150O
14、下列说法错误的是（ ）
A、一组对边平行且另一组对角相等的四边形是平行四边形
B、每组邻边都相等的四边形是菱形
C、四个角都相等的四边形是矩形
D、对角线互相垂直平分的四边形是正方形
15、依次连接矩形各边中点得到的四边形是（ ）
A、平行四边行 B、矩形 C、菱形 D、正方形
二、填空题：
1、等腰三角形一底角为50O，则顶角为 ；
2、命题“平行四边形的两组对边分别相等”的逆命题是：
；
3、若一个等边三角形的边长是4cm，则它的高为 ；
4、一元二次方程
的求根公式是
；
5、方程
的常数项是
，方程
的根是
；
6、在平行四边形ABCD中，∠ACB=∠B=50O，则∠ACD＝ ；
7、菱形的面积为120，一条对角线为10，则它的周长是 ；
8、平行四边行ABCD的周长为40，两邻边AB与AC之比为3:2，则AB＝ ；
9、依次连接 各边中点得到的四边形是矩形。
三、解答题：
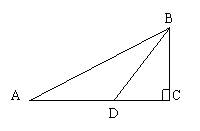1、如图，已知，在Rt△ABC中，∠C＝90O，∠A＝30O，D在AC上，且AD=BD=20，
求BC的长。
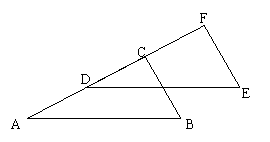2、如图，已知点A、D、C、F在同一条直线上，AD=CF，BC=EF，且BC//EF。
求证：DE//AB.
3、解下列方程：
（1）
（2）
（3）
（3）
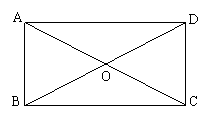4、如图，已知矩形ABCD的对角线AC与BD相交于点O，∠AOD＝120O，AB=10cm，
求BD的长。
5、如图，在Rt△ABC中，∠ACB＝90O，CM是斜边AB的中线，AM=AN，NM//AC。
求证：MN=AC。
6、当x为何值时，代数式
的值相等。
7、如图，有一面积为150m2的长方形苗圃，苗圃的一边靠墙（墙长为18m），另三边用竹篱笆围成。如果竹篱笆的长为35m，求苗圃的长和宽各为多少米？
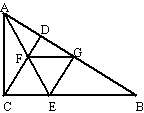
8、在△ABC中，∠ACB=90°，CD⊥AB，AE平分∠BAC交CD于F，EG⊥AB于G，
求证：四边形CEGF是菱形。
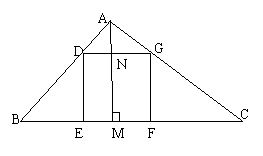9、如图，在△ABC中，AM⊥BC于D，BC＝8cm，AM=6cm，正方形DEFG的四个定点在△ABC的边上，求正方形DEFG的边长。