初三中考数学模拟练习

初三中考数学模拟练习

班级　　　　　号数　　　　　姓名　　　　　　

一、选择题：（本大题共7小题,每小题3分,共21分）

1．= （　　）

A．　　　　 B．　9　　　　 C．　－９　　　　D．　８１　

２．下列运算正确的是（　　）

Ａ．３a＋２b＝５ab　　　　　　　  Ｂ．a^６÷a^３＝a^２

Ｃ．(a^３)^２＝a^５Ｄ．（a－１）^２＝a^２－２a＋１

　　　　　　　　　　　　 2x-6<0

３．不等式组　　　　　　　　　　　的解集是（　　）

　　　　　　　　　　　　　x+5>-3

A．２＜x<３ B．－８＜x＜－３　C．－８＜x＜３　D．x＜－８或x＞３

４．如图，在平行四边形ABCD中，Ｅ是DC边的中点，　Ａ　　　　　D　　　

　　　　　　　　　 

ＡE交BD于点O．若S_△DOE=9，则S_△AOB等于（　　）　 B　　　　  C 　　　　

Ａ． 18　　 Ｂ.　27　　 Ｃ.　36　 Ｄ.  45　　 　　　　　　　　 

5．设有12只型号相同的杯子其中一等品的7只，二等品3只，三等品2只，则从中任取一只是二等品的概率是（　　）

A．　　　　B．　　　　C．　　　D．

６．在函数中，自变量的取值范围是（　　）

Ａ．x＞－１　Ｂ．x＞－１且x０　 Ｃ．x-1且x０　　 Ｄ．x０

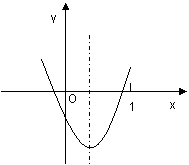
7．己知二次函数y=ax²+bx+c(a≠0)的图象如图所示，则下列结论：

① a-b+c>0

②方程ax²+bx+c=0的两之各大于零　　　　　　　 

③y随x的增大而增大

④一次函数y=ax+bc的图象一定不过第二象限

　其中正确的个数是（　　　）

　A　1个　　　　B　2个　　C　3个　　D　4个　　　　　

二、填空题：（本大题共10小题,每小题4分,共40分）

８．－２的绝对值是　　　　．

９．分解因式：a²b²－b²c²=　　　　　　　　　　  ．

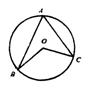
_{10．如图，已知A、B、C是⊙O上3个点，}

_{若∠BOC=120°，则∠BAC=　　　　 .}

11．一元二次方程2x²－４x－３＝０的两根为x₁、x₂，则x₁²＋x₂²＝　　　　　　 ．

12．抛物线的顶点坐标是　　　，对称轴是　　　　　　．

13．已知扇形的圆心角为120°,弧长为20,则扇形的面积是　　　　．

14．为解决药价虚高给老百姓带来的求医难的问题,国家决定对某药品分两

次降价，若设平均每次降价的百分率为x，该药品的原价为m元，降价后的

价格是y元，则y与x的函授关系式是　　　　　　　　．

15．如图，粮仓的顶部是圆锥形，这个圆锥底面周长　

为32m，母线长为7m，为防雨需要在粮仓顶部铺上油

毡，则共需油毡　　　　　　 m²（油毡接缝重合部分不计）.

16．如图，△ABC中,F为AB的中点，点D在ABC的外部，

DC＝DA，DE⊥AC于E，试说明EF与BC的关系　　　　　A

　　　　　　　　　　　．　　　　　　　　　　　 F　　E　　 D

　　　　　　　　　　　　　　　　　　　　　　Ｂ　　Ｃ

17．如图，在△ABC中，∠BAC=120，AD⊥BC　　　　Ａ

于D，且AB+BD=DC，那么∠C的度数是

 　　　　　　 ．　　　　　　　　　　　　 Ｂ　　Ｄ　　　　　　  Ｃ　

 三、解答题：（本大题共9小题,共89分）

18.化简后求值：，其中（8分）

19.解方程组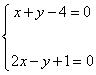：　　　 （8分）

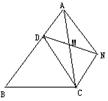
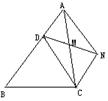20．如图,已知:D是△ABC的边AB上的一点，CN∥AB，　

DN交AC于点M，若MA＝MC．　　　　　　 　　　　　　

求证：四边形ADCN是平行四边形 (8 分)　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　 

21.（9分）某地举办乒乓球比赛的费用y(元)包括两部分:一部分是租用比赛场地等固定不变的费用b(元),另一部分是与比赛的人数x(人)成正比例,当x=20时,y=1600,当x=30时,y=2000.

(1)　求y与x之间的函授关系式.

(2)　如果有50名运动员参加比赛,且全部费用由运动员分摊,那么每名运动员需要支付多少元?

22.（10分）某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为80m²的三个项目的任务. 三个项目的面积比例和每人每分钟完成各项目的工作量如下图所示:　

　　　　　　　　　　 

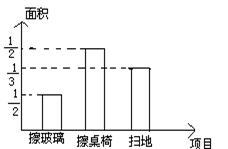
各项目面积比例　　　　　　　  每人每分钟完成各项目工作量统计图

（1）从上述统计图可知：每人每分钟能擦桌椅　　　　m²；擦玻璃、课桌椅、扫地的面积分别是　　　　  　m² 、　　　　　 m²、　　　　　  m².

（2）如果x人每分钟擦玻璃的面积是ym²，那么y关于x的函授关系式是　　　　　．

（3）他们一起完成扫地的任务后,把这13人分成两组,一组去擦玻璃，一组去擦课桌椅．如果你是卫生委员，你该如何分配这两组人数，才能最快地完成任务．

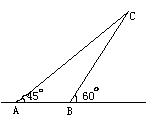23. （10分）如图,天空中有一个静止的广告　　

气球C, 从地面A 点测得C点的仰角为45°,

从地面B点测得C点的仰角为60°. 已知

AB=20, 点C和直线AB在同一铅垂平面上,

求气球离地面的高度(结果保留根号).

24.（12分）如图AB为⊙O的直径,C是O上一点,D在AB的延长线上,且

∠DCB=∠A

（1）　　　 CD与⊙O相切吗?如果相切,请加以证明;若不相切,请说明理由.

（2）　　　 若∠D=30°,BD=10cm,求⊙O的半径.

　　　　　

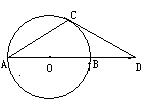
24题图　　　　　　　　　　　　　　  25题图

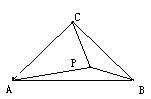
25. （10分） 如图,在等腰直角△ABC中, ∠ACB=90°, P为三角形内一点,且PA=3, PB=1, PC=2

（1）　　　 将△ACP绕C点旋转90°, 作出旋转后的△CBE.

（2）　　　 你能得到BE²=PE²+PB²这个结论吗?请说明理由.

（3）　　　 计算出∠BPC的度数.

26.如图, 函数的图象交x轴于M, 交y轴于N, 点P是直线MN上任一点,

 PQ⊥x轴, Q是垂足, 设点Q的坐标为(t,0), △POQ的面积为S.(当点P与M、N重合时, 其面积记为0).

（1）　　　 求M、N两点的坐标.

（2）　　　 分别计算当t=1和t=-1时,△ POQ的面积.

（3）　　　 试求S与t之间的函关系式.

（4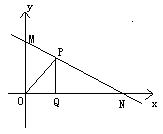）　　　 在平面直角坐标系中画出这个函数的图象,并利用图象求使得S=的点P的个数.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　　　　　

数学中考模拟试卷 

数学答题卡 　　成绩　　　　　　 　 2006.05

一、选择题 （1）　　 　　　　　　　（4）　　　　　　　　　  （7） （2）　　　　　　　　　 （5） （3）　　　　　　　　　 （6） 二、填空题： 三、解答题： （8）　　　　　　　  （12）　　　　　　　  　（16）　　　　　 　　　   （9）　　　　　　　　 (13) 　　　　　　　　　　(17)　　　　　　　　　　   （10）　　　　　　　  (14)　　　　　　 　　    (11)　　　　　　　   (15)　　　　　　  　 　  （18）（本题8分） 请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效

请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效 （19）（本题8分） （20）（本题8分） 　　　　　　　　　　　　　　　　　　　  　　　　　 　　　　　　　　　　　　　　　　　　　　　　 请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效

请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效 （21）（本题9分） (22）（本题10分） （1）从上述统计图可知：每人每分钟能擦桌椅　　　　m2；擦玻璃、课桌椅、扫地的面积分别是　　　　  　m2 、　　　　　 m2、　　　　　  m2. （2）如果x人每分钟擦玻璃的面积是ym2，那么y关于x的函授关系式是　　　　　． 请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效 各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效 （23）（本题10分） （24）（本题12分） 请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效

请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效 （25）（本题12分） 请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效

请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效 （26）（本题12分） 请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效