第27章《相似图形》练习卷
一.选择题
1.在比例尺为1:5000的地图上,甲、乙两地的距离为25cm,则甲、乙两地的实际距离是( )
A 1250km B 125km C 12.5km D 1.25km
2.如图1，
是平行四边形，则图中与
相似的三角形 共有（ ）
A１个 B ２个 C ３个 D 4个
3. 若两个图形成位似关系，则下列说法不正确的是（ ）
A每对对应点所在的直线都相交于同一点；
B两个图形上的对应线段必定平行；
C两个图形上的对应线段之比等于位似比； D两个图形的面积比等于相似比的平方；
4. 下列四组图形中不一定相似的是 ．
Ａ有一个角等于
的两个等腰三角形； Ｂ有一个角为
的两个直角三角形；
Ｃ直角三角形被斜边上的高分成的两个直角三角形；
Ｄ有一个角是
的两个等腰三角形；
5. 能判定
与
相似的条件是( )．
Ａ 
Ｂ 
，且
Ｃ 
且
Ｄ ，且
6. 一个三角形的长分别为3，5，7，另一个与它相似的三角形的最
长边是21，则其余两边之和为 ( )．
Ａ 19 Ｂ 17 Ｃ 24 Ｄ 21
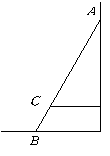
7. 如图，
是斜靠在墙上的梯子，梯脚点
距墙1.5m，梯上点
距墙1.2m，
长为0.6m，则梯子的长为 （ ）
A 2m B 2.4m C 2.7m D 3m
8.已知△ABC的三边长分别为
,
,2, △A′B′C′的两边长分别是1和
,如果△ABC与△A′B′C′相似,那么△A′B′C′的第三边长应该是( )
A B 
C 
D 
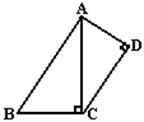
9.如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,
要使△ABC∽△CAD,只要CD等于( )
A 
B 
C 
D 
10.一个钢筋三角架三 长分别为20cm,50cm,60cm,现要再做一个与其相似的钢筋三角架,而只有长为30cm和50cm的两根钢筋,要求以其中的一根为一边,从另一根截下两段(允许有余料)作为另两边,则不同的截法有( )
A 一种 B 两种 C 三种 D 四种
二.填空题
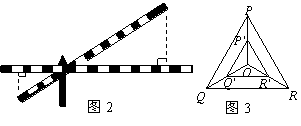
11.如图2，铁道口栏杆的短臂长为1.2m，长臂长为8m，当短臂端点下降0.6m时，长臂端点升高 m（杆的粗细忽略不计）．
12.两个相似三角形的面积之比为1∶9,小三角形的周长为4,则另一个三角形的周长为_____ .
13.在比例尺为1∶40000的平面图上，5.2平方厘米所表示的实际面积为_______平方米。
14.
ABC中，D是BC上的点，∠CAD=∠B，AC=4，CD=3，则BD= .
15.已知△ABC∽△A′B′C′，
，求△A′B′C′与△ABC的相似比是 。
16.如图3，点O是等边三角形PQR的中心，P′、Q′、R′分别是OP、OQ、OR的中点，则△P′Q′R′与△PQR是位似三角形．此时，△P′Q′R′与△PQR的位似比为 ．
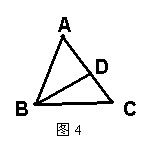
17.如图4，D为△ABC的边AC上的一点。若要使△ABD与△ACB相似，可添加条件
或 （要求写出两种方法）
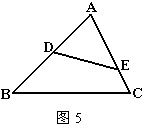
18.如图5,△ABC中,D,E分别是AB,AC上的点(DE
BC),当
或
或
时,△ADE与△ABC相似.
19.把一矩形纸片对折,如果对折后的矩形与原矩形相似,则原矩形纸片的长与宽之比为 .
 |
三.解答题
20.在方格纸中，每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.请你在如图所示的4×4的方格纸中,画出两个相似但不全等的格点三角形(要求:标明字母,并说明理由).
21.小颖测得2m高的标杆在太阳下的影长为1.2m,同时又测得一棵树的影长为3.6m,请你帮助小颖计算出这棵树的高度.
22、如图，已知AE与CD交于点B，AC∥DE.
求证：(1)△ABC∽△EDB (2)若AC=2，BC=3，BD=6，求DE的长.
 |
23.如图，已知
若
cm，
cm，试求
的长．
25.如图,测量小玻璃管口径的量具ABC,AB的长为10cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE∥AB),那么小玻璃管口径DE是多大?
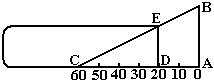
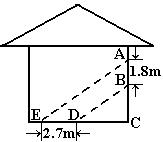
24.阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.
26.已知，如图，在⊙O中， AB是直径，CD是一条弦，且CD⊥AB于P,连结BC，AD.
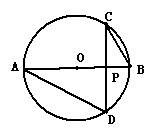求证：PC2 =PA·PB.
 | |
27.如图,△ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F.
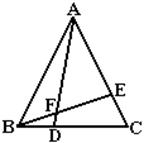(1)试说明△ABD≌⊿BCE.
(2)△AEF与△ABE相似吗?说说你的理由.
(3)BD2=AD·DF吗?请说明理由.
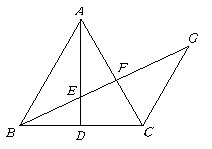28.已知：如图，等腰中，
交于
，
，
分别交
于
．求证：
.