初中数学“能力提高”培训题（6）（解直角三角形1） 姓名
一、填空题、选择题：
1． Rt△ABC中，∠C＝Rt∠，BC＝4，AB＝5，则tanB＝
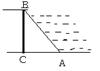
2、某水坝横断面如图1，坝高BC=5m，迎水斜坡AB的坡度为1：2，那么斜坡AB的长为
3.在Rt⊿ABC中，， AB = 6，，
则BC = __________
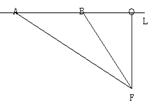
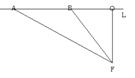
4.某酒店在装修时，在大厅的主楼梯上铺设某种红色地毯，已知这种地毯每平方米售价30元，主楼梯宽2米，其侧面如图2所示，则购买地毯至少需要__________元。
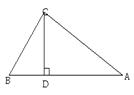
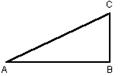
5、如图3，在△ABC中，∠ACB=90°，BC=4，AC=5，CD⊥AB，则sin∠ACD的值是________,
tan∠BCD的值是____________
|
|
|
|
图1 图2 图3 图4
7、如果∠α是等边三角形的一个内角，那么cosα的值等于 （ ）
A、
B、
C、
D、1
8、在Rt△ABC中，∠C是直角，各边的长度都分别扩大2倍，那么∠A的三角函数值（ ）
A没有变化 B分别扩大2倍 C分别扩大倍 D不能确定
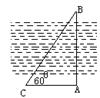
9、已知，AB为一建筑物，从地面C点用测角仪测得A的仰角为α，仪器高DC＝b，若BC＝a，则建筑物AB的高度可表示为（ ）
A、
B、
C、
D、
|
，
，则这个三角形一定是（ ）
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
二、解答题
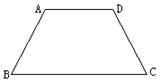
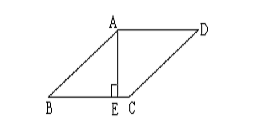
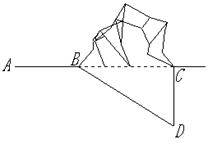
1 如图，等腰梯形ABCD中，AD∥BC，tanB=，上底AD=10，梯形的高是6，
求(1)∠B的度数；(2)下底BC的值。(结果保留根号)
|
3、如图，小王在陆地上从A地经B地到达C地总行程是14千米，这里的∠ABC为直角，且∠BAC的正切值为0.75，那么小王乘海轮从A地直接到C地的最短距离是多少千米？
|
|
于E点，
，EC=1，求四边形AECD的周长。
|
初中数学“能力提高”培训题（7）（函数1） 姓名
一、填空题：
1、函数y＝
的函数值为0时，所对应的自变量x的取值为_______________________
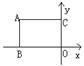2、如图，在直角坐标系中,矩形ABOC的长为3，宽为2 ，
则顶点A的坐标是（_________）.
3、点P（1，2）关于y轴的对称点A的坐标是______________，
关于x轴的对称点B的坐标是______________，关于原点O的对称点C的坐标是______________。
4、已知点M在第四象限，到x轴的距离是3，到y轴的距离是5，则M的坐标是____________。
5、已知点P（a+3，a）在第二象限，则a的取值范围是___________________
6、已知点P在第三象限,它的横坐标与纵坐标的差为1，点P的坐标可以是___________（只要写出符合条件的一个点即可）。
7、将点P（－2，1）向右平移2个单位，得到点D的坐标是______________ ，将点P向下平移3个单位，得到点F的坐标是_______________ ，将点P向右平移1个单位，再将P向上平移3个单位，得到点E的坐标是________________。
8、数轴上的点和_________是一一对应的；在平面直角坐标系中的点和______________也是一一对应的。
9、已知点A的坐标是（2，－3），AB＝4，AB∥y轴，则B的坐标是_______________
10、已知P（a，2）和Q（－1，b）关于y轴对称，则a=________,b=_____________.
11、若点P（a，b）在第四象限，则点M（b－a，b）在第_______象限。
12、已知点P（4m－9，2m＋3）在第一、三象限夹角平分线上，则m=_____；
已知点P（a－2，3a＋8）在第二、四象限夹角平分线上，则点P的坐标是______。
13、当m 时， 函数y＝（m－2）x－1是一次函数； 当m = 时， 函数y＝3x2m＋1＋3是一次函数；当m = 时，函数y＝x－m＋3是正比例函数。
14、直线y＝4x－3过点（ ，0）、（0，
）；直线y＝－
过点（ ，0）、（0， ）。
15、直线y＝2x－1与x轴交点坐标是______；与y轴交点坐标是______。与两坐标轴
所围成的三角形面积是 。
16、将直线y＝2x向下平移2个单位，得到直线__ ____；将直线y＝－2x＋3向上平移2个单位，得到直线__ ____。
17、已知函数y＝（m－1）x＋3，当m 时，y随x的增大而增大，函数图象从左到右 ；当m 时，y随x的增大而减小，函数图象从左到右 。
18、已知点（－1，m）和（2，n）都在y＝－2x＋3上，试比较m、n的大小 。
19、已知一个正比例函数的图象经过点（-2，4），则这个正比例函数的表达式是 .
20、若函数y= -2xm+2是正比例函数，则m的值是 .
21、已知一次函数y=kx+3的图象经过点（-1，2），则k= .
22、某种储蓄的月利率为0.15%，现存入1000元，则本息和y（元）与所存月数x之间的函数关系式是 .
23、出同时具备下列两个条件的一次函数表达式（写出一个即可） .
（1）y随着x的增大而减小。 （2）图象经过点（-1， 3）
24、某人用充值50元的IC卡从A地向B地打长途电话，按通话时间收费，3分钟内收费2.4元，以后每超过1分钟加收1元，若此人第一次通话t分钟（3≤t≤45），则IC卡上所余的费用y（元）与t（分）之间的关系式是
.
二、解答题：
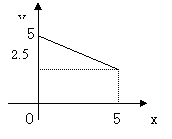
1、如图是关于x的一次函数y＝kx＋b的图象，根据图象回答：
⑴自变量x的取值范围；⑵当x取何值时，y的值最小？
⑶在⑴中x的取值范围内，y随x的增大而怎样变化？
⑷求这个一次函数的解析式。
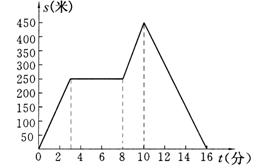
2、小明从家里出发，外出散步，到一个公共阅报栏前看了一会报后，继续散步了一段时间，然后回家。右图描述了小明在散步过程中离家的距离s（米）与散步所用时间t（分）之间的函数关系.请你根据图象回答下列问题：
①公共阅报栏离小明家有多远？
②小明看报用了多少时间？
③到达离家最远的地方是什么时间？
④返回时，小明的平均速度是多少？
初中数学“能力提高”培训题（8）（函数2） 姓名
一、填空题
1、如果正比例函数的图象经过点（2，4），那么这个函数的解析式为 。
|
|
2、点P（a,b）在第二象限，则直线y=ax+b不经过第 象限。
3、 已知一次函数y=2x+m和y=3x+2m两图象交点的横坐标为1，则m= 一次函数y=kx+b的图象经过（0，4），且与两坐标轴所围成的三角形的面积为8，则k= ，b= .
4、如果直线y=k1x+4和直线y=k2x-1的交点在x轴上，那么k1：k2= 。
5、函数y=-x+4(-2≦x≦5)的图象与x轴的交点坐标是 ，函数的最大值为 。
6、已知两条直线y1=k1x+b1和y2=k2x+b2相交与点（-3，2），并且分别经过点（-1.5，3）和（1，-2），那么这两条直线与y轴围成的三角形的面积为 。
7、某音像出版社对外出租光盘的收费方法是：每张光盘在租出后头两天每天收0.8元，以后每天收0.5元，那么一张光盘在租出后的第n天（n是大于2的自然数）应收租金为 。
二、选择题
8、若一次函数y=kx+b的图象经过点（-2，-1）和点（1，2），则这个函数的图象不经过第
象限。 A、1 B、2 C、3 D、4
|
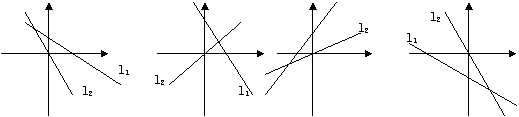
A B C D
|
|
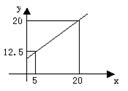
10、弹簧的长度与所挂重物的质量的关系成一次函数，如图所示，
由图可知不挂物体时弹簧的长度为 cm。
A、7 B、8 C、9 D、10
11、已知一次函数y=2x+a与y=-x+b的图象都经过A（-2，0），
且与y轴分别交于B、C两点，则⊿ABC的面积为 。
A、4 B、5 C、6 D、7
12、若直线y=2x-1与y=x-k的交点在第四象限，则k的取值范围是 。
A、k﹤0.5 B、k﹥1 C、0.5﹤k﹤1 D、以上都不对
三、解答题：
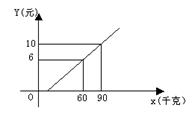
1、 某汽车客运公司规定旅客可以随身携带一定重量的行李，如果超过规定的重量，则需要购买行李票，行李票费用y（元）与行李重量x（千克）之间函数关系的图象如图所示。（1）求y与x之间的函数关系。（2）旅客最多可以免费携带多少千克的行李？
2、某工厂生产某种产品，每件产品的出厂价为50元，其成本价为25元，因为在生产过程
中，平均每生产一件产品有0.5立方米污水排放，所以为了净化环境，工厂设计两种方案对污水进行处理，并准备实施。
方案1：工厂污水先净化后排放，每处理1立方米污水所用原料费为2元，并且每月排污设备损耗费为30000元；
方案2：工厂将污水排到污水厂统一处理，每处理1立方米污水需付14元的排污费。
问：（1）设工厂每月生产x件产品，每月的利润为y元，分别求出依方案1和方案2处理污水时，y与x的函数关系式（利润=总收入-总支出）；
（2）设工厂每月生产量为6000件产品，你若作为厂长在不污染环境，又节约资金的前提下，应选用哪种处理污水的方案，请通过计算加以说明。
3、某公司在甲、乙两座仓库分别有农用车12辆和6辆。现在需要调往A县10辆，需要调往B县8辆，已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元；从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元。
（1）设乙仓库调往A县农用车x辆，求总运费y关于x的函数关系式；
（2）若要求总运费不超过900元，问共有几种调运方案？
（3）求出总运费最低的调运方案，最低运费是多少元？
初中数学“能力提高”培训题（9）（解直角三角形2） 姓名
一、填空题
1、菱形的两条对角线长为
和6，则菱形的相邻两内角分别为
度。
2、
中，
，则
=
。
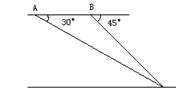
3、若由
点测得
点的仰角为36°，则由点测得点的俯角为
度。
4、铁道路基的横断面是一个等腰梯形，上底为10m，下底为13.6m，高为1.2m，则腰面的坡度为 。
二、解答题：
1、在平行四边形
中，两邻边
，且平行四边行的面积为15
，求其边长
。
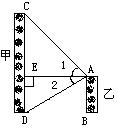2、如图,甲、乙两建筑物的水平距离为30米，从乙的顶测得甲的顶部的仰角为60°，测得甲的底部
的俯角为30°，求，两建筑物的高
。
|
|
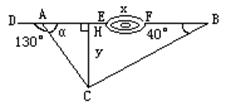
3、如图，开凿一条隧道，测得
米， 
米，
米，求隧道的长度
(精确到1米)。
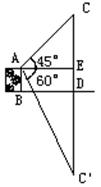
4、如图，某人在建筑物
的顶部测得一烟囱
的项端的仰角为45°，测得
在湖中的倒影
的俯角为60°。已知
米，求烟囱高(精确到1米)。
|
|
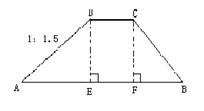
5、如图，水库大坝的断面为一梯形。已知坝顶宽
=2.8米，坝底宽
米，坝高4.2米,斜坡AD的坡度为1 : 1.5，求斜坡的坡度和斜坡的长。
|
|
6、某直升飞机于空中处观测正前方地面上控制点的俯角为
，若航向不变，飞机继续飞行1000米到达处，再测控制点的俯角为
，问飞机在处再向前飞多远时与地面控制点的距离最近？
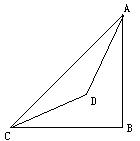7、如图，在山脚处测得山顶的仰角为，沿着倾角为的斜坡前进300米到处，测得的仰角为
，求山高。
初中数学“能力提高”培训题（10）（数据的处理） 姓名
一、填空题、选择题：
1、对某班50名学生作一次调查，得到下表
| 喜欢的体育项目 | 足球 | 篮球 | 乒乓球 | 羽毛球 |
| 人数 | 30 | 25 | 40 | 20 |
若想表示上述数据，可选用（ ）
A.扇形统计图 B.频数直方图 C折线统计图 D．以上三种均可以
2、 超市里有甲、乙、丙、丁四种牌子的酱油，标准质量都是500克，从中各抽出5袋测的质量如下，根据下列数据（单位：克）判断，质量稳定的是 （ ）
A 甲：501 500 506 510 509 B 乙：493 494 511 494 508
C 丙：503 504 499 501 500 D 丁：497 502 495 507 501
3、小明任意抛一枚硬币，连续掷了三次，每次都朝上的机会是
4、暗箱内放有大小、形状、质地相同的4个球，分别标上1、2、3、4四个号码，有放回的连续摸两次，都大于2的机会是 ，都是奇数的机会是 第一次是奇数第二次是偶数的机会是
5、2001年某中学少年队员的“小主人文具店”开业后第一季度的收人与支出情况如下图：
根据统计图填空： 月份的收入最多，是 元； 月份的支出最多，是 元；第一季度盈利大约
6、甲、乙两名跳水运动员在三米跳板跳水中平均分都是9.5分，甲的方差为0.62，乙的方差为0.45，则 的成绩稳定。
二、解答题：
1、到医院看病注射青霉素药水，医生都要给你做皮试，极少数人对青霉素药水过敏，大约也就是一千个人里有一个，即发生过敏的概率大约是0.1%，医生为什么一定要这么做呢？
2、在分别写着数字0、1、2、3的四张卡片中任意取出2张组成一个两位数，求这个两位数能被2整除的机会．
3、有甲、乙两个新品种的水稻进行杂交配系，要比较出产量较高、稳定性较好的一种，种植后各抽取5块田获取数据，其亩产量分别如下表：（单位：kg)
| 1 | 2 | 3 | 4 | 5 | |
| 甲 | 52 | 50 | 51 | 49 | 53 |
| 乙 | 51 | 51 | 51 | 48 | 54 |
（1） 哪一种品种平均单产较高？（2）哪一种品种稳定性较好？（3）据统计，应选哪一种品种做杂交配系
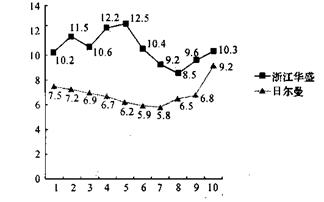4、以下统计图是浙江华盛和日尔曼公司2003年某月上旬的收盘价，分别计算它们的平均值、极差和方差，并比较这两种股票在这段时间内的涨跌情况
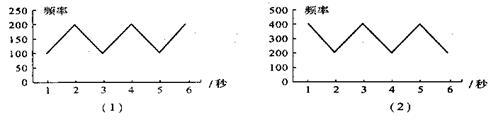
5、声音是通过空气传播的一种连续的波，叫声波．声音的强弱体现在声波压力的大小上，音调的高低体现在声音的频率上．下面是两种声音的频率图，比较（1）、（2）两组数据的平均值以及标准差，说说哪种声音的起伏大
6、为了了解高中学生的体能情况，抽了若干名学生进行引体向上次测试，将所得数据整理后，画出频数分布直方图（如右图所示），图中从左到右依次为第1、2、3、4、5组．
①共有多少名学生参加测试？
②处于哪个次数段的学生数最多？（答出是第几组即可）
③若次数在5次（含5次）以上为达标，则达标率为_____％；
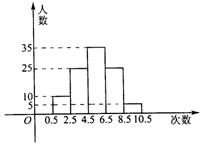④这100个数据的众数一定落在第3组吗？