初中毕业生学业考试数学试卷
数 学
考生注意：1、本学科试卷共有六道大题，满分150分，考试时量120分钟；
2、考生可带科学计算器参加考试。
一、填空题（本大题8个小题，每小题4分，满分32分）
1.
的相反数是
.
2.据统计，湖南省常德市2005年农业总产值达到24 800 000 000元，用科学计数法可表示为 元.
3.已知一元二次方程有一个根是2，那么这个方程可以是 （填上你认为正确的一个方程即可）
4.等腰梯形的上底、下底和腰长分别为4
，10，6，则等腰梯形的下底角为
度
5.多项式
与多项式
的公因式是
.
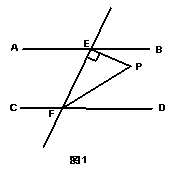
6、如图1，若AB∥CD，EF与AB、CD分别相交于点E、F，
EP⊥EF，∠EFD的平分线与EP相交于点P，且
∠BEP=40°，则∠EPF= 度.
7、在半径为10的⊙O中，圆心O到弦AB的距离为6，
则弦AB的长是 ..
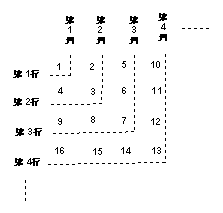
8、右边是一个有规律排列的数表，请用含
的代数式（为正整数）表示数表中
第行第列的数：
.
二、选择题（本题中的选项只有一个是正确的，请你将正确的选项填在下表中，本大题8个小题，每小题4分，满分32分）
| 题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 |
9、下列计算正确的是
（A）
（B）
（C）
（D）
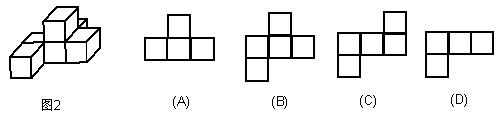
10、图2是由6个相同的小立方块搭成的几何体，那么这个几何体的俯视图是
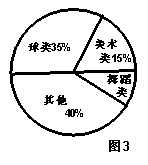
11、图3是某中学七年级学生参加课外活动人数的扇形统计
图，若参加舞蹈类的学生有42人，则参加球类活动的学
生人数有
（A）145人
（B）147人
（C）149人
（D）151人
12、根据下列表格中二次函数
的自变量
与函数值
的对应值，判断方
程
（
、
、
为常数）的一个解的范围是
|
| 6.17 | 6.18 | 6.19 | 6.20 |
|
| －0.03 | －0.01 | 0.02 | 0.04 |
（A）
（B）
（C）
（D）
13、下列命题中，真命题是
（A）两条对角线相等的四边形是矩形
（B）两条对角线垂直的四边形是菱形
（C）两条对角线垂直且相等的四边形是正方形
（D）两条对角线相等的平行四边形是矩形
14、已知
、
、
是反比例函数
的图象上的三点，且
，则
、
、
的大小关系是
（A）
（B）
（C）
（D）
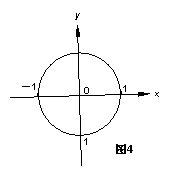15、如图4，在直角坐标系中，⊙O的半径为1，则直线
与⊙O的位置关系是
（A）相离
（B）相交
（C）相切
（D）以上三种情形都有可能
16、若用（1），（2），（3），（4）四幅图象分别表示变量之间的关系，
将下面的
对应的图象排序：
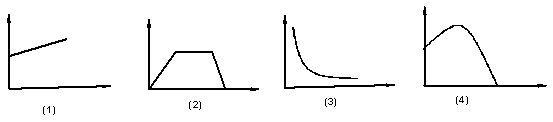
（a）面积为定值的矩形（矩形的相邻两边长的关系）
(b)运动员推出去的铅球（铅球的高度与时间的关系）
(c)一个弹簧不挂重物到逐渐挂重物（弹簧长度与所挂重物质量的关系）
(d)某人从A地到B地后，停留一段时间，然后按原速返回（离开A地的距离与时间的关系），其中正确的顺序是
（A）（3）（4）（1）（2） （B）（3）（2）（1）（4）
（C）（4）（3）（1）（2） （D）（3）（4）（2）（1）
三、（本小题4个小题，每小题6分，满分24分）
17、计算：
18、先化简代数式：
，然后选取一个使原式有意义的的值代入
求值
19、有2个信封，每个信封内各装有四张卡片上分别写有1、2、3、4四个数，另一个信封内的四张卡片上分别写有5、6、7、8四个数，甲、乙两人商定了一个游戏，规则是：从这两个信封中各随机抽取一张卡片，然后把卡片上的两个数相乘，如果得到的积大于20，则甲获胜，否则乙获胜。
（1）请你通过列表（或画树状图）计算甲获胜的概率（4分）
（2）你认为这个游戏公平吗？为什么？（2分）
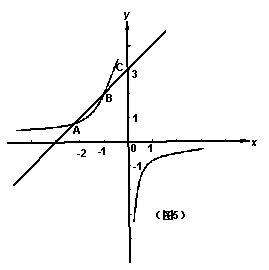20、如图5，已知反比例函数
的
图象经过点A（－2，1），一次函数
的图象经过点C（0，3）与点A、且与
反比例函数的图象相交于另一点B。
（1）分别求出反比例函数与一次函数的解析式；
（4分）
（2）求点B的坐标。（2分）
四、（本大题2个小题，每小题8分，满分16分）
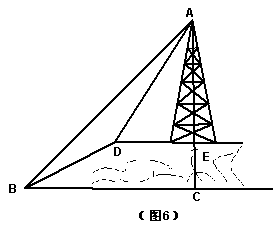21、如图6，小山的顶部是一块平地，在这块平地上有一高压输电的铁架，小山的斜坡的坡度
，斜坡BD的长是50米，在山坡的坡底B处测得铁架顶端A的仰角为
45°，在山坡的坡顶D处测得铁架顶端A 的仰角为60°。
（1）求小山的高度；（4分）
（2）求铁架的高度。（
，精确到0.1米）（4分）
22、如图7，P是等边△ABC内的一点，连结PA、PB、PC，以BP为边作∠PBQ=60°，且BQ=BP，连结CQ。
（1）观察并猜想AP与CQ之间的大小关系，并证明你的结论。（4分）
（2）若PA∶PB∶PC=3∶4∶5，连结PQ，试判断△PQC的形状，并说明理由。（4分）
五、（本大题2个小题，每小题10分，满分20分）
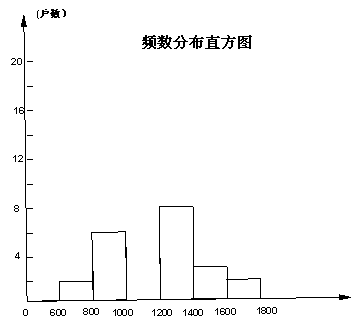23、在今年“五一”长假期间，某学校团委会要求学生参加一项社会调查活动。八年级学生小青想了解她所居住的小区500户居民的家庭收入情况，从中随机调查了40户居民家庭的收入情部（收入取整数，单位：元），并绘制了如下的频数分布表和频数分布直方图。
| 分组 | 频数 | 频率 |
| 600～799 | 2 | 0.050 |
| 800～999 | 6 | 0.150 |
| 1000～1199 | 0.450 | |
| 1200～1399 | 9 | 0.225 |
| 1400～1599 | ||
| 1600～1800 | 2 | 0.050 |
| 合计 | 40 | 1.000 |
根据以上提供的信息,解答下列问题:
（1）补全频数分布表;(3分)
（2）补全频数人布直方图;(2分)
（3）这40户家庭收入的中位数落在哪一个小组？（2分）
（4）请你估计该居民小区家庭收入较低（不足1000元）的户数大约有多少户？（3分）
24、某电器经营业主计划购进一批同种型号的挂式空调和电风扇。若购进8台空调和20台电风扇，需要资金17400元，若购进10台空调和30台电风扇，需要资金22500元。
（1）求挂式空调和电风扇每台的采购价各是多少元？（5分）
（2）该经营业主计划购进这两种电器共70台，而可用于购买这两种电器的资金不超过30000元，根据市场行情，销售一台这样的空调可获利200元，销售一台这样的电风扇可获利30元。该业主希望当这两种电器销售完时，所获得的利润不少于3500元。试问该经营业主有哪几种进货方案？哪种方案获利最大？最大利润是多少？（5分）
六、（本大题2个小题，每小题13分，共26分）
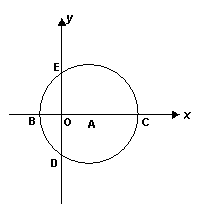
25、如图8，在直角坐标系中，以点A
为圆心，以
为半径的圆与轴相交于点B、C，与轴相交于点D、E
（1）若抛物线
经过C、D两点，求抛物线的解析式，并判断点B是否在该抛物线上.（6分）
（2）在（1）中的抛物线的对称轴上求一点P，使得△PBD的周长最小.（3分）
（3）设Q为（1）中的抛物线上的一点，在抛物线对称轴上是否存在这样的点M，使得四边形BCQM为平行四边形.若存在，求出点M的坐标；若不存在，说明理由。（4分）
26、把两块全等的直角三角板ABC和DEF叠放在一起，使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合，其中∠ABC=∠DEF=90°，∠C=∠F=45°，AB=DE=4，把三角板ABC固定不动，让三角板DEF绕点O旋转，设射线DE与射线AB相交于点P，射线DF与射线BC相交于点Q.
（1）如图9，当射线DF经过点B，即点Q与点B重合时，易证△APD∽△CDQ。此时，AP·CQ= .（2分）
（2）将三角板DEF由图9所示的位置绕点O沿逆时针方向旋转，设旋转角度为α，其
，问AP·CQ的值是否改变？说明你的理由.（5分）
（3）在（2）的条件下，设CQ=，两块三角板重叠部分的面积为，求与的函数关系式.（图10、图11供解题用）（6分）
