初中毕业生学业考试数学试题
一、选择题(每小题3分，共30分，在每小题给出的四个选项中，只有一项符合题目要求)
1．若家用电冰箱冷藏室的温度是4℃，冷冻室的温度比冷藏室的温度低22℃，则冷冻室的温度是( )
(A)l8℃ (B)-26℃ (C)-22℃ (D)-1 8℃
2．今年“五一”黄金周，宁波市接待游客人数创历年新高，达216．3万人次，用科学记数法可表示为( )
(A)2．163×106人次 (B)2．163×107人次
(C)0．2 163 ×1 07人次(D)216．3 ×1 04人次
3．如图，水平放置的圆柱形物体，中间有一细棒，则此几何体的左视图是( )
4．某足球评论员预测：“6月l 3日进行的世界杯小组意大利队对加纳队的比赛，意大利队有80％的机会获胜”与“80％的机会获胜"意思最接近的是( )
(A)意大利队肯定会赢这场比赛
(B)意大利队肯定会输这场比赛
(c)假如这两支球队进行10场比赛，意大利队会赢8场左右
(D)假如这两支球队进行l 0场比赛，意大利队恰好会赢8场
5．使式子意义的
的取值范围为：( )
(A)x>2 (B)x≥2 (C)x≥O (D)x<2
6．将1 00个个体的样本编成组号为①～⑧的八个组，如下表：
| 组 号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ |
| 频数 | 1 4 | 1 1 | 1 2 | l 3 | ■ | 1 3 | l 2 | l O |
那么第⑤组的频率为 ( )
(A)14 (B)l5 (C)0．114 (D)0．15
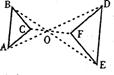
7．如图，△ABC与△DEF是位似图形，相似比为2：3，已知AB=4，则DE的长等于 ( )
(A)6 (B)5 (c)9 (D)8/3
8．如图，为保持原图案的模式，应在空白处补上( )
同时抛掷两枚1元的硬币，菊花图案都朝上的概率是( )
(A)1/2 (B)1/3 (c)1/4 (D)1/5
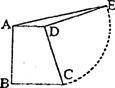
10.如图，直角梯形ABCD中，AD∥BC，AB⊥BC，AD=3，BC=5，将腰DC绕点D逆时针方向旋转90°至DE，连结KE，则△ADE的面积是( )
(A)1 (B)2 (C)3 (D)4
二、填空题(每小题3分，共24分)
11.计算：
= ▲
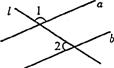
12．如图，直线a∥b，∠1=130°，则∠2= ▲ 度．
13.已知反比例函数的图象过点(-3，1)，则此函数的解析式为 ▲
14．依法纳税是公民应尽的义务．《个人所得税法》规定：每月总收入减去1600元后的余额为应纳税所得额，应纳税所得额不超过500元的按5％纳税；超过500元但不超过2000元的部分按1 0％纳税，若职工小王某月税前总收人为2000元，则该月他应纳税 ▲ 元．
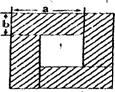
15．长、宽分别为a、b的矩形硬纸片拼成的一个“带孔”正方形如图所示。利用面积的不同表示方法，写出一个代数恒等式 ▲ 。
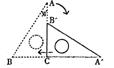
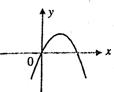
16．若二次函数y-ax2+2x+a2-1(a≠0)的图象如图所示，则a的值是 ▲
17．如图，斜边长为6cm,∠A=30°的直角三角板ABC绕点C’顺时针方向旋转90°至△A'B'C'的位置，再沿CB向左平移使点B'落在原三角板ABC的斜边AB上．则三角板向左平移的距离为 ▲ cm．
l 8．已知∠BAC=45°，一动点O在射线AB上运动(点O与点A不重合)，设OA=x，如果半径为l的⊙O与射线AC只有一个公共点，那么x的取值范围是 ▲
三、解答题
1 9．解不等式组
20．已知x=l+
，求代数式
的值．
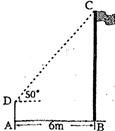
21.如图，在离旗杆6m的A处，用测角仪测得旗杆顶端c的仰角为50°．已知测角仪高AD=1．5 m，求旗杆BC的高．(结果是近似数，请你自己选择合适的精确度)
如果你没有带计算器，也可选用如下数据：
sin50°≈0．7660， cos50°≈O．6428， tan50°≈1．1 92 ，cot50°≈O．8391
22．2005年12个省市月最低工资标准的统计表如下．(单位：元)。
| 省市名称 | 北京 | 天津 | 上海 | 江苏 | 杭州 | 宁波 | 深圳 | 大连 | 厦门 | 陕西 | 辽宁 | 甘肃 |
| 月最低工资 | 580 | 590 | 690 | 690 | 670 | 620 | 690 | 500 | 620 | 490 | 450 | 340 |
(1)求以上12个数据的中位数、众数、平均数和极差.
(2)如果你是劳动管理部门的一员，会更关注(1)中的哪一个指标?为什么?
23.利用图象解一元二次方程x2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x2和直线y=2x+1，两图象交点的横坐标就是该方程的解．
(1)请再给出一种利用图象求方程x2-2x-1=0的解的方法
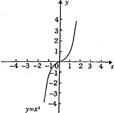
(2)已知函数y=x3的图象(如图)：求方程x3-x-2=0的解．(结果保留2个有效数字)
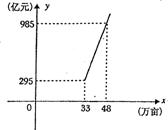
24.宁波市土地利用现状通过国土资源部验收，我市在节约集约用地方面已走在全国前列．1996--2004年，市区建设用地总量从33万亩增加到48万亩，相应的年GDP从295亿元增加到985亿。 宁波市区年GDP y(亿元)与建设用地总量x(万亩)之间存在着如图所示的一次函数关系．
(1)求y关于x的函数关系式．
(2)据调查2005年市区建设用地比2004年增加4万亩，如果这些土地按以上函数关系式开发使用，那么2005年市区可以新增GDP多少亿元?
(3)按以上函数关系式，我市年GDP每增加1亿元，需增建设用地多少万亩?(精确到0．001 万亩)
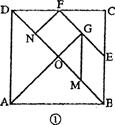
25．对正方形ABCD分划如图①，其中E、F分别是BC、CD的中点，M、N、G分别是OB、OD、EF的中点，沿分划线可以剪出一副由七块部件组成的“七巧板”．
(1)如果设正方形OGFN的边长为l，这七块部件的各边长中，从小到大的四个不同值分别为l、x1、x2、x3，那么x1= ▲ ；各内角中最小内角是 ▲ 度，最大内角是 ▲ 度；用它们拼成的一个五边形如图②，其面积是 ▲ ，
(2)请用这副七巧板，既不留下一丝空自，又不相互重叠，拼出2种边数不同的凸多边形，画在下面格点图中，并使凸多边形的顶点落在格点图的小黑点上(格点图中，上下、左右相邻两点距离都为1)．
(3)某合作学习小组在玩七巧板时发现：“七巧板拼成的凸多边形，其边数不能超过8”．你认为这个结论正确吗?请说明理由．
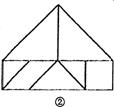
注：不能拼成与图①或②全等的多边形!
