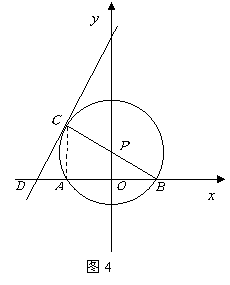初中毕业数学升学考试(新课标)
注意事项:
1.本试题满分120分,考试用时120分钟;
2.答题前将密封线内的项目填写清楚;
3.考试结束后将试卷按页码顺序排好,全部上交.
| 题号 | 一 | 二 | 三 | 总分 | |||||||
|
|
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | ||
| 得分 | |||||||||||
一、选择题(本大题10个小题,每小题3分,共30分.在每小题给出的四个选项中只有一个是正确的,请把正确选项的标号填在下面的选项栏内.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 选项 |
1.计算![]() 的结果是( )
的结果是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
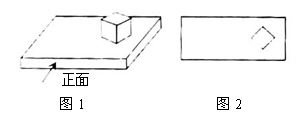 2.如图1,在一个长方体上放着一个小正方体,若这个组合体的俯视图是图2,则这个组合体的左视图是( )
2.如图1,在一个长方体上放着一个小正方体,若这个组合体的俯视图是图2,则这个组合体的左视图是( )
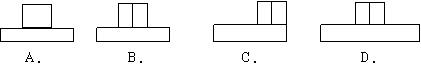 |
3.若家用电冰箱冷藏室的温度是4℃,冷冻室比冷藏室的温度低22℃,则冷冻室的温度为( )
A.![]() ℃ B.
℃ B.![]() ℃ C.
℃ C.![]() ℃ D.
℃ D.![]() ℃
℃
4.在等边三角形、等腰梯形、平行四边形、正五边形中,是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
5.已知圆柱的底面半径为4,高为6,则这个圆柱的侧面积为( )
A.24 B.24![]() C.48 D.48
C.48 D.48![]()
6.将点![]() 向下平移1个单位后,落在函数
向下平移1个单位后,落在函数![]() 的图象上,则
的图象上,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.为了解决老百姓看病难的问题,卫生部门决定大幅度降低药品价格,某种常用药品降价![]() 后的价格为
后的价格为![]() 元,则降价前此药品价格为( )
元,则降价前此药品价格为( )
A.![]() 元 B.
元 B.![]() 元 C.
元 C.![]() 元 D.
元 D.![]() 元
元
8.图3是测量一物体体积的过程:
步骤一,将![]() 的水装进一个容量为
的水装进一个容量为![]() 的杯子中.
的杯子中.
步骤二,将三个相同的玻璃球放入水中,结果水没有满.
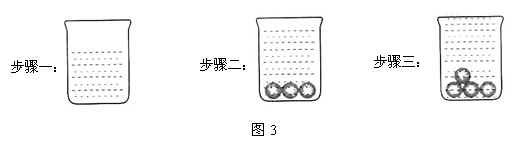 步骤三,同样的玻璃球再加一个放入水中,结果水满溢出.
步骤三,同样的玻璃球再加一个放入水中,结果水满溢出.
根据以上过程,推测一颗玻璃球的体积在下列哪一范围内?![]()
A.![]() 以上,
以上,![]() 以下 B.
以下 B.![]() 以上,
以上,![]() 以下
以下
C.![]() 以上,
以上,![]() 以下 D.
以下 D.![]() 以上,
以上,![]() 以下
以下
9.国家为九年义务教育期间的学生实行“两免一补”政策,下表是我市某中学国家免费提供教科书补助的部分情况.
|
| 七 | 八 | 九 | 合计 |
| 每人免费补助金额(元) | 110 | 90 | 50 |
|
| 人数(人) | 80 | 300 | ||
| 免费补助总金额(元) | 4000 | 26200 |
如果要知道空白处的数据,可设七年级的人数为![]() ,八年级的人数为
,八年级的人数为![]() ,根据题意列出方程组为( )
,根据题意列出方程组为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 10.如图4,在直角梯形
10.如图4,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从
从![]() 点出发,由
点出发,由![]() 沿边运动,则
沿边运动,则![]() 的最大面积为( )
的最大面积为( )
A.10 B.12 C.14 D.16
二、填空题(本大题8个小题,每小题3分,共24分)
11.一元二次方程![]() 的根是 .
的根是 .
12.不等式组![]() 的解集是 .
的解集是 .
![]()
![]()
![]()
![]()
![]()
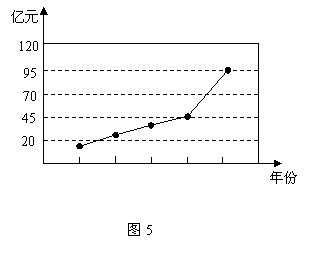 13.图5是根据我市2001年至2005年财政收入绘制的折线统计图,观察统计图可得:同上年相比我市财政收入增长速度最快的年份是 年,比它的前一年增加 亿元.
13.图5是根据我市2001年至2005年财政收入绘制的折线统计图,观察统计图可得:同上年相比我市财政收入增长速度最快的年份是 年,比它的前一年增加 亿元.
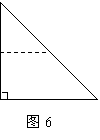
14.如图6,将一张等腰直角三角形纸片沿中位线剪开可以拼出不同形状的四边形,请写出其中两个不同的四边形的名称: .
15.如图7,在数轴上,![]() 两点之间表示整数的点有 个.
两点之间表示整数的点有 个.
 | |||||
 | |||||
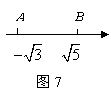 | |||||
16.如图8,![]() 是
是![]() 上的三点,
上的三点,![]() ,
,![]() ,那么
,那么![]() 的半径等于 .
的半径等于 .
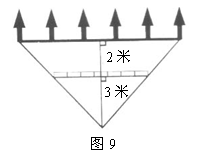
17.如图9所示,某校宣传栏后面2米处种了一排树,每隔2米一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3米处,正好看到两端的树干,其余的4棵均被挡住,那么宣传栏的长为 米.(不计宣传栏的厚度)
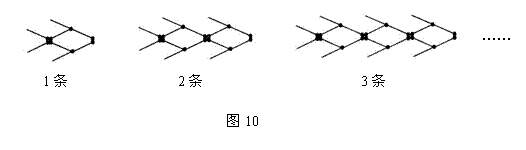
18.如图10是小明用火柴搭的1条、2条、3条“金鱼”![]() ,则搭
,则搭![]() 条“金鱼”需要火柴 根.
条“金鱼”需要火柴 根.
 |
三、解答题(本大题8个小题,共66分.解答时要写出必要的文字说明、演算步骤或推证过程)
19.(本小题满分5分)
化简:![]()
20.(本小题满分7分)
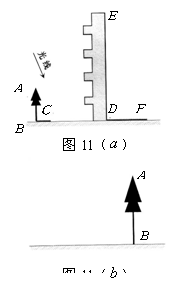
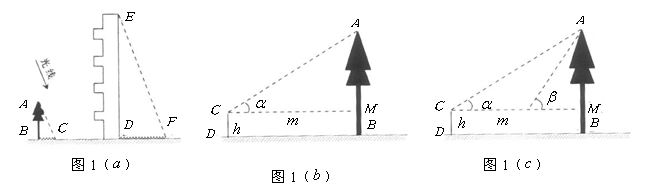
高为12米的教学楼![]() 前有一棵大树
前有一棵大树![]() ,如图11(
,如图11(![]() ).
).
(1)某一时刻测得大树![]() 、教学楼
、教学楼![]() 在阳光下的投影长分别是
在阳光下的投影长分别是![]() 米,
米,![]() 米,求大树
米,求大树![]() 的高度;
的高度;
(2)现有皮尺和高为![]() 米的测角仪,请你设计另一种测量大树
米的测角仪,请你设计另一种测量大树![]() 高度的方案,要求:
高度的方案,要求:
①在图11(![]() )中,画出你设计的测量方案示意图,并将应测量的数据标记在图上(长度用字母
)中,画出你设计的测量方案示意图,并将应测量的数据标记在图上(长度用字母![]() 表示,角度用希腊字母
表示,角度用希腊字母![]() 表示);
表示);
 ②根据你所画出的示意图和标注的数据,求出大树的高度(用字母表示).
②根据你所画出的示意图和标注的数据,求出大树的高度(用字母表示).
21.(本小题满分8分)
我市某中学为了解九年级300名学生的理化实验操作水平,从中随机抽取30名学生进行测试.下表是这30名学生的测试成绩(分):
| 4 | 5 | 7 | 6 | 3 | 7 | 9 | 4 | 5 | 7 |
| 7 | 3 | 7 | 5 | 6 | 8 | 7 | 5 | 6 | 8 |
| 6 | 7 | 4 | 10 | 5 | 6 | 7 | 3 | 9 | 4 |
(1)请你设计一张统计表,能够清楚反映出各成绩的人数分布情况;
(2)求出这30名学生成绩的平均数、众数;
(3)如果测试成绩6分以上(包括6分)为合格,请估计300名学生中成绩合格的约有多少人?
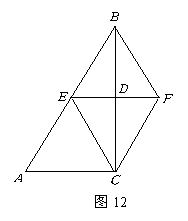 22(本小题满分8分)
22(本小题满分8分)
如图12,在![]() 中,
中,![]() ,
,![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,且
,且![]() .
.
(1)求证:四边形![]() 是菱形.
是菱形.
(2)当![]() 的大小满足什么条件时,菱形
的大小满足什么条件时,菱形![]() 是正方形?请回答并证明你的结论.
是正方形?请回答并证明你的结论.
23.(本小题满分7分)
如图13,有两个可以自由转动的均匀转盘![]() .转盘
.转盘![]() 被平均分成
被平均分成![]() 等份,分别标上
等份,分别标上![]() 三个数字;转盘
三个数字;转盘![]() 被平均分成4等份,分别标上
被平均分成4等份,分别标上![]() 四个数字.有人为甲、乙两人设计了一个游戏规则;自由转动转盘
四个数字.有人为甲、乙两人设计了一个游戏规则;自由转动转盘![]() 与
与![]() ,转盘停止后,指针各指向一个数字,将指针所指的两个数字相加,如果和是6,那么甲获胜,否则为乙获胜.
,转盘停止后,指针各指向一个数字,将指针所指的两个数字相加,如果和是6,那么甲获胜,否则为乙获胜.
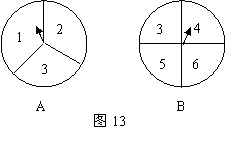 你认为这样的游戏规则是否公平?如果公平,请说明理由;如果不公平,怎样修改规则才能使游戏对双方公平?
你认为这样的游戏规则是否公平?如果公平,请说明理由;如果不公平,怎样修改规则才能使游戏对双方公平?
24.(本小题满分9分)
某产品每件成本10元,在试销阶段每件产品的日销售价![]() (元)与产品的日销售量
(元)与产品的日销售量![]() (件)之间的关系如下表:
(件)之间的关系如下表:
|
| 20 | 25 | 30 | 35 |
|
|
| 30 | 25 | 20 | 15 |
|
(1)在草稿纸上描点,观察点的分布,确定![]() 与
与![]() 的函数关系式.
的函数关系式.
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
25.(本小题满分10分)
如图14(![]() ),两个不全等的等腰直角三角形
),两个不全等的等腰直角三角形![]() 和
和![]() 叠放在一起,并且有公共的直角顶点
叠放在一起,并且有公共的直角顶点![]() .
.
(1)将图14(![]() )中的
)中的![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 角,在图14(
角,在图14(![]() )中作出旋转后的
)中作出旋转后的![]() (保留作图痕迹,不写作法,不证明).
(保留作图痕迹,不写作法,不证明).
(2)在图14(![]() )中,你发现线段
)中,你发现线段![]() ,
,![]() 的数量关系是 ,直线
的数量关系是 ,直线![]() ,
,![]() 相交成 度角.
相交成 度角.
(3)将图14(![]() )中的
)中的![]() 绕点
绕点![]() 顺时针旋转一个锐角,得到图14(
顺时针旋转一个锐角,得到图14(![]() ),这时(2)中的两个结论是否成立?作出判断并说明理由.若
),这时(2)中的两个结论是否成立?作出判断并说明理由.若![]() 绕点
绕点![]() 继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.
继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.

26.(本小题满分12分)
如图15,点![]() 在
在![]() 轴上,
轴上,![]() 交
交![]() 轴于
轴于![]() 两点,连结
两点,连结![]() 并延长交
并延长交![]() 于
于![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 轴于
轴于![]() ,且
,且![]() 的半径为
的半径为![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求证:![]() 是
是![]() 的切线;
的切线;
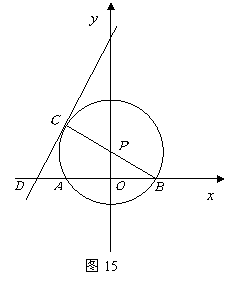 (3)若二次函数
(3)若二次函数![]() 的图象经过点
的图象经过点![]() ,求这个二次函数的解析式,并写出使二次函数值小于一次函数
,求这个二次函数的解析式,并写出使二次函数值小于一次函数![]() 值的
值的![]() 的取值范围.
的取值范围.
初中毕业升学考试数学试题参考答案及评分说明(新课标)
(一)阅卷评分说明
1、正式阅卷前先进行试评,在试评中认真阅读参考答案,明确评分标准,不得随意拔高或降低评分标准.试评的试卷必须在阅卷后期全部予以复查,防止阅卷前后期评分标准宽严不一致.
2、评分方式为分步累计评分,解答过程的某一步骤发生笔误,只要不降低后继部分的难度,而后继部分再无新的错误,后继部分可评应得分数的![]() ;若是几个相对独立的得分点,其中一处错误不影响其它得分点的评分.
;若是几个相对独立的得分点,其中一处错误不影响其它得分点的评分.
3、最小记分单位为1分,不得将评分标准细化至1分以下(即不得记小数分)
4、解答题题头一律记该题的实际得分,不得用记负分的方式记分.对解题中的错误须用红笔标出,并继续评分,直至将解题过程评阅完毕,并在最后得分点处标上该题实际得分.
5、本参考答案只给出一至两种解法,凡有其它正确解法都应参照本评分说明分步确定得分点,并同样实行分步累计评分.
6、合理精简解题步骤者,其简化的解题过程不影响评分.
(二)参考答案及评分标准
一、选择题(本大题10个小题,每小题3分,共30分.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 选项 | C | B | A | C | D | A | D | C | D | B |
二、填空题(本大题8个小题,每小题3分,共24分)
11.![]() ,
,![]() 12.
12.![]() 13.2005 50(约50)(填对一空给2分)
13.2005 50(约50)(填对一空给2分)
14.等腰梯形、矩形(长方形)、平行四边形中任选两个即可(填对一个给2分)
15.4 16.2 17.6 18.![]()
三、解答题(本大题8个小题,共66分)
19.(本小题满分5分)
解:![]()
![]() ································································································ 2分
································································································ 2分
![]() ············································································································· 3分
············································································································· 3分
![]() ························································································································ 4分
························································································································ 4分
![]() ······························································································································· 5分
······························································································································· 5分
20.(本小题满分7分)
解:(1)连结![]() ,
,![]() ,则
,则![]()
![]() ················································································································· 2分
················································································································· 2分
![]()
即大树![]() 高是
高是![]() 米······································································································ 3分
米······································································································ 3分
(2)解法一:
①如图1(![]() )(标注
)(标注![]() ,
,![]() ,画草图也可给相同的分)··············································· 5分
,画草图也可给相同的分)··············································· 5分
②在![]() 中,
中,![]() ··························································· 6分
··························································· 6分
![]() ····································································································· 7分
····································································································· 7分
解法二:
①如图1(![]() )(标注
)(标注![]() ,画草图也可给相同的分)··········································· 5分
,画草图也可给相同的分)··········································· 5分
②![]()
![]() ································································································· 6分
································································································· 6分
![]() ····························································································· 7分
····························································································· 7分
21(本小题满分8分)
(1)统计表如下:
| 成绩 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 3 | 4 | 5 | 5 | 8 | 2 | 2 | 1 |
································································································································ 3分
(表格格式正确给1分;填数、计数正确给2分,错误一处扣1分,扣完2分为止.画正字统计以及其它符合题意的统计表均可按此标准给分.如果统计出现错误,下面(2),(3)的评分按“评分说明”中的第2条规定酌情评分.)
(2)平均数![]() ·················· 4分
·················· 4分
![]() ······································································································· 5分
······································································································· 5分
众数为![]() ················································································································ 6分
················································································································ 6分
(3)![]() ···································································································· 7分
···································································································· 7分
答:估计有180人合格.························································································ 8分
22.(本小题满分8分)
(1)证法一:如图2
![]() 垂直平分
垂直平分![]() ,
,![]() ,
,![]() ···················································· 2分
···················································· 2分
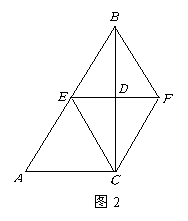
![]()
![]() ··················· 3分
··················· 3分
![]() 四边形
四边形![]() 是菱形··············································· 4分
是菱形··············································· 4分
证法二:如图2
![]() 垂直平分
垂直平分![]() ,
,![]() ,
,![]() ········· 1分
········· 1分
![]()
![]() ····················· 2分
····················· 2分
![]() ································································ 3分
································································ 3分
![]() 四边形
四边形![]() 是菱形··············································· 4分
是菱形··············································· 4分
(2)解法一:
当![]() 时,菱形
时,菱形![]() 是正方形.································································ 6分
是正方形.································································ 6分
![]() ,
,![]()
![]() ··················································· 7分
··················································· 7分
![]()
![]() 菱形
菱形![]() 是正方形.······················································································ 8分
是正方形.······················································································ 8分
解法二:
当![]() 时,菱形
时,菱形![]() 是正方形.································································ 6分
是正方形.································································ 6分
![]() ,
,![]()
![]() ······················································ 7分
······················································ 7分
![]()
![]()
![]() 菱形
菱形![]() 是正方形.······························································ 8分
是正方形.······························································ 8分
23.(本小题满分7分)
解:不公平.················································································································ 2分
![]() (和为6)
(和为6)![]() ,甲、乙获胜的概率不相等············································· 5分
,甲、乙获胜的概率不相等············································· 5分
![]() 不公平.(无列表或树状图不扣分)
不公平.(无列表或树状图不扣分)
规则改为:和是6或7,甲胜;否则乙胜.····························································· 7分
(和为奇数,甲胜;和为偶数,乙胜;或和小于7,甲胜;和大于等于7,乙胜.答案不唯一.) 列 表
|
| 3 | 4 | 5 | 6 |
| 1 | 4 | 5 | 6 | 7 |
| 2 | 5 | 6 | 7 | 8 |
| 3 | 6 | 7 | 8 | 9 |
24.(本小题满分9分)
解:(1)设函数关系式为![]() ,根据题意得(方程组较多):
,根据题意得(方程组较多):![]() ········ 2分
········ 2分
解之得:![]() ··································································································· 3分
··································································································· 3分
![]() ······································································································· 4分
······································································································· 4分
(2)设每日的销售利润为![]() 元,则:
元,则:
![]() ································································································· 6分
································································································· 6分
![]() ························································ 7分
························································ 7分
![]() ······················································································ 8分
······················································································ 8分
![]() 当
当![]() 时,
时,![]() (当
(当![]() 时,
时,![]() ,同样给分)············· 9分
,同样给分)············· 9分
答:每件产品的销售价定为30元时,每日销售利润最大是![]() 元.
元.
25.(本小题满分10分)
解:(1)如图3(![]() )(
)(![]() 字母位置互换扣1分,无弧扣1分,不连结
字母位置互换扣1分,无弧扣1分,不连结![]() 扣1分,扣完为止) 2分
扣1分,扣完为止) 2分
(2)![]() ;
;![]() (每空1分)································································ 4分
(每空1分)································································ 4分
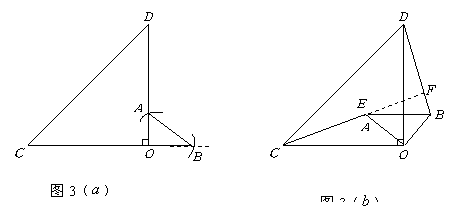 (3)成立.如图3(
(3)成立.如图3(![]() )
)
![]()
![]()
即:![]() (或由旋转得
(或由旋转得![]() )········································ 5分
)········································ 5分
![]()
![]()
![]() ··········································· 6分
··········································· 6分
![]() ·········································································································· 7分
·········································································································· 7分
延长![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() (下面的证法较多)
(下面的证法较多)
![]() ,
,![]() ·························································· 8分
·························································· 8分
![]()
![]()
![]() ···················· 9分
···················· 9分
旋转更大角时,结论仍然成立.··········································································· 10分
26.(本小题满分12分)
解:(1)如图4,连结![]()
![]()
![]() ······································································ 1分
······································································ 1分
![]()
![]() ,
,![]() ······································· 2分
······································· 2分
![]() 是
是![]() 的直径
的直径![]() (也可用勾股定理求得下面的结论)
(也可用勾股定理求得下面的结论)
![]() ,
,![]()
![]() ················································· 3分
················································· 3分
![]() ,
,![]() ,
,![]() (写错一个不扣分)········································ 4分
(写错一个不扣分)········································ 4分
(2)![]() 过
过![]() 点
点![]()
![]() ·········································· 5分
·········································· 5分
![]() 当
当![]() 时,
时,![]()
![]()
![]()
![]() ··········································· 6分
··········································· 6分
![]() ,
,![]()
![]()
![]()
![]()
![]() (也可用勾股定理逆定理证明)······························· 7分
(也可用勾股定理逆定理证明)······························· 7分
![]() 是
是![]() 的切线······················································································· 8分
的切线······················································································· 8分
(3)![]() 过
过![]() 点
点
![]()
![]() ···························································· 9分
···························································· 9分
![]() ························································································· 10分
························································································· 10分
因为函数![]() 与
与![]() 的图象交点是
的图象交点是![]() 和点
和点![]() (画图可得此结论) 11分
(画图可得此结论) 11分
所以满足条件的![]() 的取值范围是
的取值范围是![]() 或
或![]() ············································· 12分
············································· 12分