初中九年级(下)第一阶段考试数学试卷
班级 姓名 座号 得分
 | |||
一、选择题(每小题4分,共20分)
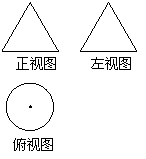
1.如果某物体的三视图是如图所示的三个图形,
那么该物体的形状是( )
A.圆柱 B.三棱锥
C.正立的圆锥 D.横放的圆锥
2.在比例尺为1:5000的地图上,两地的距离为25cm,则这两地的实际距离是 ( )
A. 1250km B. 125km C. 12.5km D. 1.25km
3. 在Rt△![]() 中,
中,![]() ,
,![]() A、
A、![]() B、
B、![]() C所对的边分别为
C所对的边分别为![]() 、b、c,则下列各式中错误的是 ( )
、b、c,则下列各式中错误的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.把二次函数![]() 配方成为( )
配方成为( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
5. 能判定![]() 与
与![]() 相似的条件是( ).
相似的条件是( ).
A.![]() B.
B.![]() ,且
,且![]()
C.![]() 且
且![]() D.
D.![]() ,且
,且![]()
二、填空题(每小题5分,共25分)
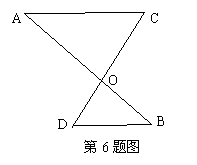
6.如图,已知:AC∥BD,请写出三组成比例线段的比例式: .
7.若抛物线![]() 经过原点且开口向下,则k的值等于_______.
经过原点且开口向下,则k的值等于_______.
8.已知抛物线![]() 与x轴的交点坐标为(-3,0)和(5,0),则它的对称轴是直线x = .
与x轴的交点坐标为(-3,0)和(5,0),则它的对称轴是直线x = .
9.如图,小明在操场上距离旗杆9米的![]() 处,用测角仪测得旗杆
处,用测角仪测得旗杆![]() 的顶端
的顶端![]() 的仰角为
的仰角为![]() ,已知测角仪
,已知测角仪![]() 的高为1.4米,那么旗杆
的高为1.4米,那么旗杆![]() 的高为 米.(结果保留三个有效数字,
的高为 米.(结果保留三个有效数字,![]() )
)
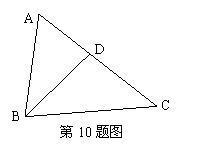
10.如图,D为△ABC的边AC上的一点,∠ABD=∠C,若AD = 4,DC = 5,则AB = .
 | |||
 | |||

三、解答题(每小题8分,共40分)
11.计算:![]()
 12.如图,
12.如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,求AC的长及tanB的值.
,求AC的长及tanB的值.
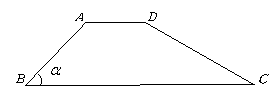
13.水库拦水坝的横截面是梯形,如图所示,坝顶宽AD
=6m,坝高8m,迎水坡DC的坡度![]() ,背水坡AB的坡角
,背水坡AB的坡角![]() .求迎水坡的坡长DC和坝底的宽BC.
.求迎水坡的坡长DC和坝底的宽BC.
 |
|
14.已知二次函数![]() 的图像经过A(0,1),B(2,-1)两点.
的图像经过A(0,1),B(2,-1)两点.
(1)求![]() 和
和![]() 的值; (2)试判断点P(-1,2)是否在此函数图像上.
的值; (2)试判断点P(-1,2)是否在此函数图像上.
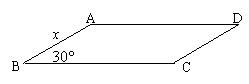 15.(1)如图,已知平行四边形ABCD的周
15.(1)如图,已知平行四边形ABCD的周
长为8cm,∠B=30. 若边长AB=xcm.
则□ABCD的面积ycm2与x的函数关系
 式是
.
式是
.
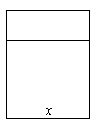
(2)如图,用6m长的材料,做一个有横档
的矩形窗子,为使透进的光线最多,那么
这个窗子的宽x应为_______m.
四、解答题(每小题8分,共32分)
 16. Rt△ABC中∠C =
16. Rt△ABC中∠C =![]() ,AC =4,BC =5,以AC为斜边作直角三角形ACD,当△ACD与△ABC相似时求AD的长.
,AC =4,BC =5,以AC为斜边作直角三角形ACD,当△ACD与△ABC相似时求AD的长.
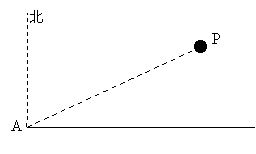
17.一艘轮船自西向东航行,在A处测得小岛在北偏东![]() 且与船的距离为16海里的P处,已知小岛周围
且与船的距离为16海里的P处,已知小岛周围![]() 海里的圆形区域内是暗礁区,问船继续向东航行是否有触礁危险?若有,船自A处开始至少沿东偏南多少度方向航行才安全?
海里的圆形区域内是暗礁区,问船继续向东航行是否有触礁危险?若有,船自A处开始至少沿东偏南多少度方向航行才安全?
 |
18.△ABC是等边三角形,点D,E分别在BC,AC上,且BD = CE,AD与BE相交于点F.
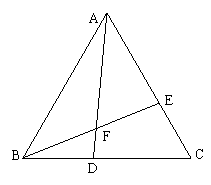 (1)求证:△ABD≌△BCE. (2) 求证:
(1)求证:△ABD≌△BCE. (2) 求证:![]() .
.
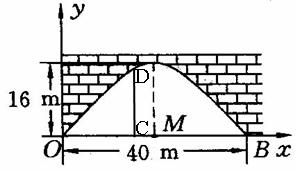
19.如图,有一个抛物线的拱形立交桥,这个桥拱的最大高度为16m,跨度为40m,现把它放在如图所示的直角坐标系里,点![]() 是OB的中点,若要在离点
是OB的中点,若要在离点![]() 5m的C处垂直竖一根铁柱CD支撑这个拱顶,铁柱应取多长?
5m的C处垂直竖一根铁柱CD支撑这个拱顶,铁柱应取多长?
![]()
五、解答题(第20题10分, 第21题11分, 第22题12分,共33分)
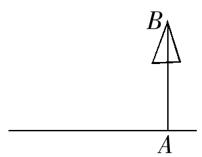
20.小明想测量校园内一棵不可攀的树的高度.由于无法直接度量![]() 两点间的距离,请你用学过的数学知识按以下要求设计一种测量方案.
两点间的距离,请你用学过的数学知识按以下要求设计一种测量方案.
(1)在图中画出测量图案;
(2)写出需要测量的数据(测量数据用字母表示);
(3)计算![]() 间的距离(写出求解或推理过程,结果用字母表示).
间的距离(写出求解或推理过程,结果用字母表示).
 |
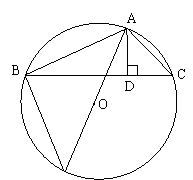
21.在⊙O的内接![]() 中,AE是⊙O 的直径,
中,AE是⊙O 的直径,![]() ,
,![]() ,垂足为
,垂足为![]() ,且
,且![]() ,设⊙O的半径为
,设⊙O的半径为![]() ,
,![]() 的长为
的长为![]() .
.
(1) 求证△ABE ∽△ADC (2)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)当![]() 的长等于多少时,⊙O的面积最大,并求出⊙O的最大面积.
的长等于多少时,⊙O的面积最大,并求出⊙O的最大面积.
|
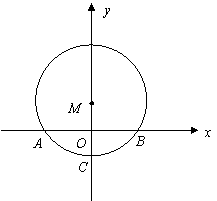
(1)求圆心![]() 的坐标;
的坐标;
(2)求经过![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(3)在(2)中的抛物线上是否存在一点![]() ,使
,使![]() 和
和![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.