中三月考试卷
一、 选择题(4＊5＝20分)
1. 在直角坐标系中，点（3，－2）在（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
2. 在△ABC中，∠C＝90。，BC＝3，AC＝4，则sinA的值等于（ ）
A、
B、
C、
D、
3. 函数y=-2x+1的图象大致是（ ）
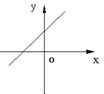
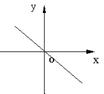
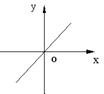
A、 B、 C、 D、
4. 若分式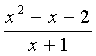
的值为0，那么x的值为（ ）
A、x=-1或2
B、x=0 C、x=2
D、x=-1
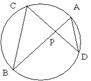
5. 如图，弦AB和CD相交于P，∠B＝30。，
∠APD＝80。，∠A＝＿＿
A、30。 B、50。 C、70。 D、110。
二、填空题(4*10=40分)
6. 如果方程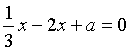
有实数根，那么a的取值范围是＿＿
7. 已知在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，则⊙O的半径为＿＿＿＿
8. 抛物线y=x2-2x-1项点坐标是＿＿＿＿
9. 计算sin45。－tan60。＝＿＿＿＿
10. 若一次函数y=（m-1）x+m-2的图象经过点(1,2)，则m=_______
11. 如图，已知圆心角∠AOB=100。，则圆周角∠ACB=________
12.
抛物线y=-6x2+3的对称轴是_____________
13.
在Rt△ABC中，∠C＝90。，sinA=，则sinB=_______
14.
函数
的自变量x的取值范围是___________
15.
已知x1，x2是方程x2-x-1=0的两个根，则
的值是______
三、解答题上(8*5=40分)
16. 二中的校办工厂现在年产值是15万元，如果每增加100元投资，一年可增加250元产值，那么总产值y(万元)与新增加的投资额x(万元)之间的函数关系是什么？如果增加1.5万元投资，年产值可达到多少？
17. 已知直线经过点(-4，9)和点(6,3)，求直线解析式，并画出这条直线
18.
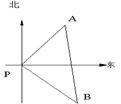如图，一艘海轮位于灯塔P的北偏东60。的A处，它沿正南方向航行70海里后，到达位于灯塔P的南偏东30。的B处，这时，海轮所在B处距离灯塔P有多远？
19.
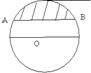在直径为130cm的圆铁片上切去一块高为32cm的弓开铁片(如图)，求弓形的弦AB的长
20. 一公司成立三年来，累积向国家上交利税1400万元，其中第一年交只有200万元，求上交利税的平均年增长率。
21. 已知二次函数的图象经过(-1，-1)，(0,2)，(1,1)三点，求函数解析式，并指出图象的开口方向，对称轴项点坐标。
22.
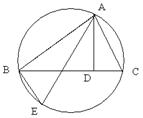如图，AD是△ABC的高，AE是△ABC的外接圆直径，求证：AB·AC=AE·AD
23.
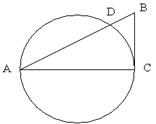如图，△ABC中，∠ACB=90。，以AC为直径的圆交斜边AB于D，AC=4cm，BC=3cm，求AD的长