初三数学测试卷
(考生注意：本卷共24题，满分150分)
一、选择题（本题共10题，每题4分，共40分）
1、计算（-2）3的值等于（ ）
A、－6 B、6 C、－8 D、8
2、式
有意义，则x的取值范围是（ ）
A．3<x<≤4 B.3<x<4 C.3≤x≤4 D.3≤x≤4
3、设汽车前灯电路上的电压保持不变（U＝12V），则选用灯泡的电阻R（Ω）与通过灯
泡的电流强度I（A）之间的函数图象大致是（ ）
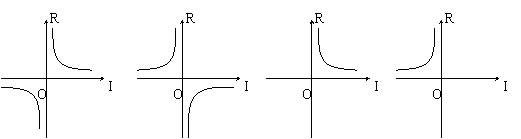
（A） （B） （C） （D）
4、分式
＝0,则x的值为（ ）
A.2 B.±2 C.-2 D. ±4
5、关于x的方程ax2—3x＋2＝2x2 是一元二次方程，则a的取值范围是（ ）
A.a≠2 B.a≠-2 C.a≠2 D.a≠±2
6、下列命题是真命题的是 （ ）
A.两条直线被第三条直线所截，同位角相等.
B.面积相等的两个三角形是全等三角形.
C.如果a是整数,那么a是有理数.
D.如果a是有理数,那么a是整数
7、设“●、■、▲”分别表示三种不同的物体，如图所示，前两架天平保持平衡，如果要使第三架也平衡，那么“？”处应放“■”的个数为 ( )
A、5 B、4 C、3
D、2
8、若0<a<1,则点M(a－1,a)在第（ ）象限。
A、第一象限 B、第二象限 C、第三象限 D、第四象限
9、如图9（1），P时反比例函数y=
在第一象限分支上的一个动点，PA⊥x轴，随着x的逐渐增大，△APO的面积将（ ）
A、增大 B、减小 C、不变 D、无法确定
10、如图10（2），l1∥l2，∠1＝1050，∠2＝1400，则∠3＝（
）
A、550 B、600 C、 650 D、700
|
| ||||||
 | ||||||
 | ||||||
| ||||||
二、填空题（本题共5题，每题4分，共20分）
11、直线y=2x-1不经过第 象限。
12、写出一个反比例函数，让它的函数值在每一个象限内，随着自变量的增大而减小
13、-
的相反数的倒数是
14、化简：
＝
15、在关于
x1 x2 x3的方程组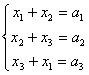
中，已知a1>a2>a3,那么将x1 x2 x3从大到小排列起来应该是
三、解答题（本大题共6小题，其中15，16每题8分，17，18每题9分，19，20每题10分，共34分）
16、先化简，再求值：
[(x-y)2+(x+y)(x-y)]÷2x,其中x=3,y=-1.5
17、已知关于x的方程x2-2(m+1)x+m2=0
(1)、当m取什么值时，原方程有实数根；
(2)、对m选取一个合适的非零整数，使原方程有两个实数根，并求这两个实数根的平方和。
18已知反比例函数
（k≠0）的图象与直线y=2x的一个交点为（2，m）求这个反比例函数的解析式和两交点的坐标。
19、
水池内装有12
的水，如果从排水管中每小时流出x的水，则流过y小时就可以把水放完，⑴ y与x的函数关系式 ⑵ 画出函数的图象 ⑶ 当x=6时，求时间y的值。
20、某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为80m2的三个项目的任务. 三个项目的面积比例和每人每分钟完成各项目的工作量如下图所示:
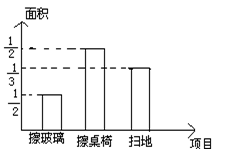
各项目面积比例 每人每分钟完成各项目工作量统计图
（1）从上述统计图可知：每人每分钟能擦桌椅 m2；擦玻璃、课桌椅、扫地的面积分别是 m2 、 m2、 m2.
（2）如果x人每分钟擦玻璃的面积是ym2，那么y关于x的函数关系式是 ．
（3）他们一起完成扫地的任务后,把这13人分成两组,一组去擦玻璃，一组去擦课桌椅．如果你是卫生委员，你该如何分配这两组人数，才能最快地完成任务。
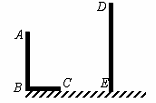
21．如图，AB和DE是直立在地面上的两根立柱.AB=5m，某一时刻AB在阳光下的投影BC=3m.
（1）请你在图中画出此时DE在阳光下的投影；
（2）在测量AB的投影时，同时测量出DE在阳光下的投影长为6m，请你计算DE的长.
 |
四、本题满分12分。
22、某中学为筹备校庆活动，准备印制一批校庆纪念册。该纪念册每册需要10张8开大小的纸，其中4张为彩页，6张为黑白页。印刷该纪念册的总费用由制版费和印刷费两部分组成，制版费与印数无关，价格为：彩300元/张黑白页50元/张；印刷费与印数的关系见下表：
| 印数a（单位：千册） | 1≤a＜5 | 5≤a≤10 |
| 彩色（单位：元/张） | 2.2 | 2.0 |
| 黑白（单位：元/张） | 0.7 | 0.6 |
（1）印制这批纪念册的制版费为＿＿＿＿元；
（2）若印制2千册，则共需多少费用？
（3）如果该校希望印数至少为4千册，总费用至多为60 000元，求印数的取值范围。（精确到0.01千册）
五、本题满分12分
23、某通讯器材公司销售一种市场需求较大的新型通讯产品．已知每件产品的进价为40元，每年销售该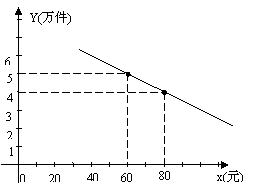
种产品的总开支（不含进价）总计120 万元．在销售过程中发现，年销售量y（万件）与销售单价x（元）之问存在着如图所示的一次函数关系．
⑴求y关于x的函数关系式；
⑵试写出该公司销售该种产品的年获利z（万元）关于销售单价x（元）的函数关系式（年获利＝年销售额一年销售产品总进价一年总开支）．当销售单价x为何值时，年获利最大？并求这个最大值；
⑶若公司希望该种产品一年的销售获利不低于40万元，借助⑵中函数的图象，请你帮助该公司确定销售单价的范围．在此情况下，要使产品销售量最大，你认为销售单价应定为多少元？
六、本题满分12分。
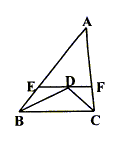24、 已知：如图23（1）所示，D是∠ABC的平分线和∠ACB的角平分线的交点，过点D作EF//BC，交AB于E，交AC于F。
（1）请你确定EF、BE、CF三者之间的关系，并加以证明。
|
（2）如图23（2）所示，当点D为∠ABC的外角的角平分线和∠ACB的外角的角平分线的交点时，EF、BE、CF三条线段还满足上面的关系吗？若满足，直接写出关系式；若不满足，请写出新的关系式并加以证明。
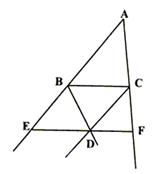
图23（2）
（3）如图23（3）所示，当点D为∠ABC的角平分线和∠ACB外角平分线的交点时，EF、BE、CF三条线段还满足上面的关系吗？若满足，直接写出关系式；若不满足，请写出新的关系式并加以证明。
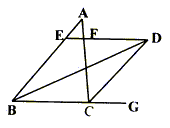
图23（3）