初三数学第一学期期末调研测试试卷
(卷面总分150分,考试时间120分钟)
一、选择(每题3分,计30分.请将每题唯一正确答案的代号填入题前括号内)
( )1.在Rt△ABC中,∠C=90
.则sinB=
A.
B.
C.
D.
( )2.已知：以x为未知量的一元二次方程的二次项系数等于1,它的两根之和为1,两根之积为-1.则该方程可写为
A.
-x+1=0 B.-x-1=0 C.+x+1=0 D.+x-1=0
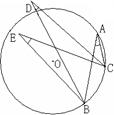
( )3.如图,点A、B、C在⊙O上,点D在⊙O外,点E在⊙O内，
∠A、∠D、∠E的大小分别为
、
、
.则有
A.
B.
C.
D.
( )4.在以点O为坐标原点的直角坐标系内,有一个半径为1的⊙O与一点P(
,0)(-1＜＜0).则点M(0,
)
A.在⊙O 内 B.在⊙O上 C.在⊙O外 D.不在⊙O 内
( )5.半径分别为1、2、3的三个圆两两相外切,则此三个圆的圆心的连心线构成的三角形面积等于
A.9 B.8 C.7 D.6
( )6.半径为6的圆中,圆心角(0＜＜90)的余弦值为
.则角所对的弦长等于
A.4
B.10
C.8
D.6
( )
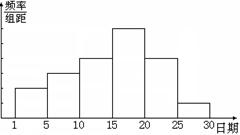7.在某中学开展的综合实践活动中,九年级(1)班进行了小制作评比.作品上交时间为11月1号至11月30号.评委会把同学们上交作品的件数按5天一组分组统计,绘制了如右方的频率分布直方图,已知图中从左至右矩形高的比为2:3:4:6:4:1,第三组频数为12.经过评比,第四组、第六组分别有10件、2件作品获奖.若第四组、第六组的获奖率分别为m、n,则
A.m＞n B.m=n C.m＜n D.m、n的大小关系无法确定
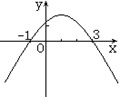( )8.如图,为一个二次函数y=
+bx+c(≠0)的图象.观察
此抛物线,欲使函数y的值非负,则自变量x的取值范围必须
且只须为
A.-1≤x≤3 B.x＜-1或x＞3
C.x≤-1或x≥3 D.-1＜x＜3
( )9.某班准备到郊外野营,为此向商店订了帐篷.如果下雨与不下雨是等可能的,能否准时收到帐篷也是等可能的.只要帐篷如期运到,他们就不会淋雨.则下列说法正确的是
A.一定不会淋雨 B.淋雨机会为
C.淋雨机会为 D.淋雨机会为
( )10.观察某个二次函数y=+bx+c(≠0)的图象,可获得两点信息：⑴抛物线的对称轴在y轴的右侧；⑵在抛物线对称轴的左侧,函数y的值随自变量x值的增大而减小.又已知该二次函数对应的一元二次方程+bx+c=0没有实数根.则、b、c值的正、负为
A.＞0、b＞0、c＞0 B.＞0、b＜0、c＜0
C.＞0、b＜0、c＞0 D.＞0、b＞0、c＜0
二、填空(每空3分,计27分)
11.在⊙O中,弦AB的长为8,圆心O到AB的距离为3.则⊙O的半径为 .
12.在菱形ABCD中,两条对角线AC、BD相交于点O.可得AC⊥BD,AO=OC且BO=OD.其理由为 （注：理由要叙述得详细、具体）.
13.抛物线y=-2(x+1)
-3的顶点坐标为
.
14.已知二次函数
=-2x+3与一次函数
=3x-1.欲使=,则自变量x的值能且只能等于
.
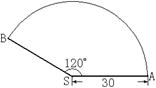
15.如图,扇形的半径为30,圆心角为120,用它做成一个圆锥模型的侧面.则这个圆锥的高为
(计算结果保留根号).
16.在Rt△ABC中,已知∠C为直角,且
∠A=
.则cos∠A= .
17.一个水库养了某种鱼10万条,从中随机地捕了10条,分别称得它们每条的质量如下(单位：500g)：2.3 2.1 2.2 2.1 2.2 2.6 2.5 2.4 2.3 2.4.试根据此样本,通过计算估计水库中这种鱼的总重量约为 ㎏.
18. 若点A(-2,0)和点B(4,b)在抛物线y=2(x-m)+h上,且关于它的对称轴对称.则
m=
.
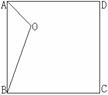
19. 在如图所示的正方形ABCD内任取一点O,连结AO、BO,得
△ABO.如果正方形ABCD内每一点被取到的可能性都相同.则△ABO
为钝角三角形的概率等于 .
三、解答题(共9题,计93分)
20.(本题8分)
不用计算器计算、求值
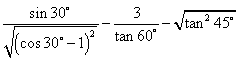.注意：在计算过程中,若有无理数,必须保留根号进行根式的运算.
21.(本题8分,每小题4分)
下面是今年与前年在大致相同条件下饲养的10头猪的体长数据（单位：cm）
前年 112 110 110 117 113 122 125 124 119 127
今年 111 122 115 123 114 115 118 114 116 115
⑴求出前年饲养的10头猪的体长数据的中位数与今年饲养的10头猪的体长数据的众数；⑵哪年饲养的10头猪的体长比较一致？为什么？
22.(本题10分.⑴⑶两小题各3分,第⑵题4分)
已知关于x的一元二次方程+bx+c=0(≠0).
⑴当=1、b=7、c=-18时,试用十字相乘法解方程(要求写出十字相乘的竖式)；
⑵当=3、b=-3、c=-2时,试用公式法解方程 (要求：用计算器求方程的近似解,解精确到百分位).
⑶若=1、b为任意实数、c＜0,试考察方程实数根的情况(要求写出详细的考察过程).
23.(本题10分.第⑴题4分,第⑵题6分)
用一根长8m铝合金型材制作一个如图所示的“日”字形的矩形窗框(不计损耗, 且不计铝合金型材的宽度).⑴求：当宽与高各是多少时,窗户透光面积为2.5
；⑵能否制作成一个透光面积为3的矩形窗框？限用二次函数的知识详细地论述其中的道理.
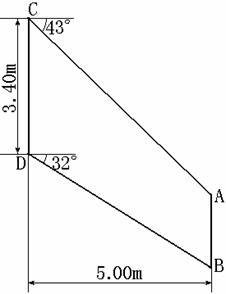
24.(本题9分)
某型号的机翼形状如图所示.根据图中数据列式用计算器计算AC、AB的长度(计算结果保留三个有效数字).
25.(本题9分)
如图,是一块未知圆心,已知半径为1的圆铁皮,现在该圆铁皮内用直尺与圆规裁剪出一个面积最大的矩形,试问必须如何作图画线(作图不写作法,但要保留作图痕迹).作图后要计算出它的面积.
26.(本题9分)
两个水平相当的选手在决赛中相遇,决赛采用五局三胜制,胜者获得全部奖金,前三局打成2∶1时比赛因故终止.有人提出按2∶1分配奖金,你认为这样合理吗？为什么（要求写出详细的推理过程）？
27.(本题10分.第(1)题3分,第(2)题2分,第(3)题5分)
如图,在下列四个圆上分别有1个点、2个点、3个点、4个点.试观察这几个图形,解答下列三个问题：
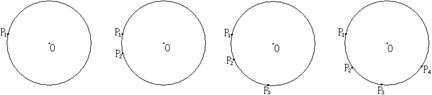
（1）若连结每个圆上的各点得到弦,试求4个圆中分别可以得到几条弦；
（2）在上面每个圆中,若以第(1)题中点的个数（n）与弦的条数(y)分别为直角坐标系中一个点的横、纵坐标,试在下面直角坐标系中描出相应的各点（n,y）；
（3）猜一猜第（2）题中所得各点会在某一函数的图象上吗？如果在,求出该函数的解析式,并求出n=10时,弦的条数y.若不在,试说明理由.
28.(本题9分)
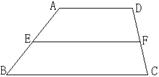如图,在梯形ABCD中,已知：AD∥BC,E、F分别是AB、DC的中点.
求证：EF∥BC,EF=(BC+AD).
29.(本题11分.第⑴题4分,第⑵题7分)
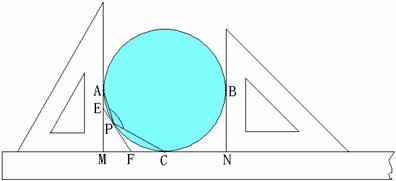
如图,已知：带有阴影的圆为一个圆形工件,两直角三角板与直尺分别和圆形工件相切于A、B、C三点,两直角三角板均有一条直角边与直尺边缘重合.试解答下列两个问题：
⑴连接切点A、B,那么线段AB必过圆形工件的圆心,为什么？
⑵已知点P为
上的一个动点.①过点P作圆形工件的切线EF,分别与AM、MC交于E、F两点.试比较△MEF的周长与圆形工件直径的长短.要求写出详细的比较过程；②连结PA、PC,试求∠APC的大小.
