初三数学试卷

初三数学试卷

第I卷

一、选择题（3分×分，将正确答案的序号填在题后表格里）

1、3^-1的相反数是　

A、3　　　　　　　　　　　 B、-3　　　　

C、　　　　　　　　　　  D、-

　2、下列运算正确的是

A、3x²+2x³=5x⁵　　　　　　  B、(-x²)²=-x⁴

C、x⁵·x²=x⁷　　　　　　　  D、x⁶÷x²=x³

　3、一个由四舍五入得到的数是56.20万，它精确到了

A、万位　　　　　　　　　  B、百位　　　

C、十分位　　　　　　　　  D、百分位

　4、右图是由一些相同的小正方体构成的几何体的三视图，在这个几何体中，小正方体的个数是

A、7　　　　 B、6　

C、5　　　　 D、4

　5、已知点P是直角坐标系中二象限内离原点距离为1的点，且OP与x轴的夹角为60°，则点P关于y轴对称点的坐标为

A、（，）　　　　　　 B、（-，）　

C、（，）　　　　　　 D、（-，-）

　6、不等式组　　2x－4＜0的解集在数轴上表示正确的是

　　　　　  　　 X+1≥0

 

　7、已知，反比例函数y=的图象上两点A（x₁,y₁）,B(x₂,y₂)。当x₁＜0 ＜x₂时有y₁ ＜y₂，则m的取值范围是

A、m＜0　　　　B、m＞0　　　　  C、m＜　　　　D、m＞

　8、给出下列命题

  ⑴一组数不可能有两个众数；

⑵数据0，-1，1，2，-1的中位数是1；

⑶将一组数据中的每个数据都加上（或减去）同一个常数后，方差恒不变；

⑷已知2，-1，0，x₁ ，x₂的平均数是1，则x₁+ x₂=4。

其中错误的个数是

A、0个　　　　  B、1个　　　　  C、2个　　　　 D、3个

　9、式子（m－n）化为最简根式，正确的是

A、－　　 B、　　　 C、　　  D、－

　10、已知下列命题“

⑴对角线相等的四边形的矩形；

⑵有两边和其中一边上的高对应相等的两个三角形全等；

⑶有两边和其中一边上的中线对应相等的两个三角形全等；

⑷在同圆或等圆中若圆周角不等，则它们所对的弦也不等。

其中不正确的有

A、只有⑴⑵　　　 B、⑴⑵⑶　　　　C、⑴⑵⑷　　 D、⑵⑶⑷

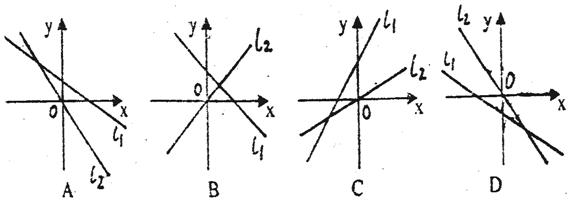
　11、在同一坐标系中，直线ι₁:y=(k-2)x+k和ι₂:y=kx的位置可能是

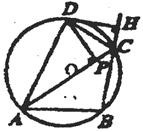
　12、如图，圆内接△ABC的外角∠ACH的平分线与⊙O交于点D，DP⊥AC，垂足为点P，DH⊥BH，垂足为H。下列结论中，⑴CH=CP，

⑵，⑶AP=BH，⑷DH为⊙O的切线，其中一

定成立的是

A、⑴、⑵、⑷　　　　　　 B、⑴、⑶、⑷　　

C、⑵、⑶、⑷　　　　　　 D、⑴、⑵、⑶

请将第I卷选择题的正确答案的序号填入下表。

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

第II卷

二、填空题（4分×5=20分）

13、分解因式x²－xy－2y²－x－y=　　　　　　　　  　　　　　　　　　　

14、在某小山的东侧A庄有一热气球，因受西风的影响，以35米/分速度沿与水平方向成75°角方向飞行，40分钟后到达C处，此时气球上的人发现气球与山顶P及小山西侧的B庄在一条直线上，并测得B庄的俯角为30°，又在A庄测得山顶P的仰角为45°，则A、B两庄间的水平距离为　　　　米。

14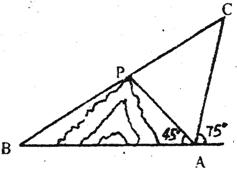题　15题

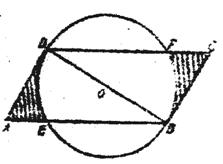
15、如右图所示，在平行四边形ABCD中，AB=4，AD=2，BD⊥AD，以BD为直径的⊙O交AB于E，交CD于F，则平行四边形ABCD被⊙O所截得的阴影部分面积为　　　　　　　　　 。

16、某商品的进价为8元，若以10元出售，则每天可售出100件，如果每件涨价1元，其销售量就会减少10件，为了达到每天的销售利润为350元，且又能减少该商品的积压，那么，这种商品的销售价应定为　　　　  元。

17、两个反比例函数 y=， y=，在第

一象限内的图象如右图所示。点P₁、P₂、P₃……

P₂₀₀₅在反比例函数y=的图象上，它们横坐标

分别是x₁ 、x₂ 、x₃……x₂₀₀₅，纵坐标分别是1，

3，5……共2005个连续奇数，过点P₁、P₂、P₃

……P₂₀₀₅分别作y轴的平行线，与y=图象交

点依次是Q₁（x₁、y₁）、Q₂(x₂、y₂)、Q₃(x₃、Y₃)

……Q₂₀₀₅(x₂₀₀₅、y₂₀₀₅),则y₂₀₀₅=　　　　　  。

三、解答题（5分+5分+9分+9分+12分+14分=64分）

　 18、（本题满分5分）先化简，后求值。

　 （x－y+）(x+y－)其中x=　　y=

19、（本题满分5分）解方程

(x+)²－+=0

20、（本题满分9分）某电脑公司现有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑，希望中学从甲、乙两种品牌的电脑中各选购一种型号的电脑。⑴写出所有选购方案（利用树状图或列表法表示）

⑵如果⑴中各种选购方案被选中的可能性相同，那么，A型电脑被选中的概率是多少？

⑶现知希望中学购买甲、乙两种品牌电脑共36台（价格表如图），恰好用了10万元人民币，其中，甲品牌电脑为A型号电脑，求购买A型号的电脑有几台？

××电脑公司

电脑价格（元） A型：6000　　　B型：4000 C型：2500　　　D型：5000 E型：2000

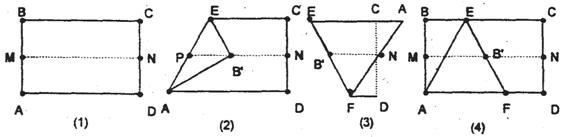
21、（本题满分9分）取一张矩形的纸进行折叠，具体操作过程如下：第一步：先把矩形ABCD对折，折痕为MN，如图⑴。第二步：再把点B叠在折痕MN上，折痕为AE，点B在MN上的对应点B′，得Rt△A B′E，如图⑵。第三步：沿EB线折叠得折痕EF，如图⑶。利用展开的图形⑷探究：

⑴△AEF是什么三角形？证明你的结论；

⑵设矩形长AD=a，宽AB=b，对于任一矩形，按上述方法是否都能折出这种三角形，若不能，请找出当a与b满足什么条件时一定能折出这种三角形？

22、（本题满分12分）由于电力紧张，我市决定对工厂实行鼓励错峰用电，规定：在每天7：00至24：00为用电高峰期，电价为a元/度，每天0：00至7：00为用电平稳期，电价为b元/度，下表为某厂4、5月份的用电量和电费的情况统计表：

⑴若4月份在平稳期的电量占当月用电量的，5月份在平稳期的用电量占当月用电量的，求a、b的值。

⑵若6月份该厂预计用电20万度，为将电费控制在10万元至10.6万元之间（不含10万元和10.6万元），那么该厂6月份在平稳期的用电量占当月用电量的比例应在什么范围内？

⑶经预算部门预测：该厂6月份每用一度电，可创造利润5元的产品一件。为了使该厂获得更好的生产效应，该厂决定拿出x万元的资金进行线路改造，改造后的用电量是预计用电量的y倍，且y=－x²+x+，试写出6月份的利润S（万元）与改造费x（万元）之间的函数关系？并计算当改造费为多少万元时，该厂获得的利润最大？最大利润是多少？

月份	用电量（万度）	电费（万元）
4	12	6.4
5	16	8.8

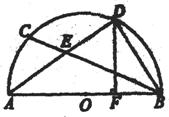
23、（本题满分10分）如图，AB为O的直径，D为弧BC的中点，连结BC交AD于点E，DF⊥AB于F。

⑴求证：BD²=AD·DE

⑵如果tanA=，DF=16，求DE的长。

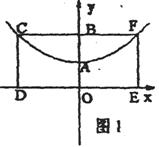
24、（本题满分14分）如图⑴，已知抛物线的顶点为A（0，1），矩形CDEF的顶点C、F在抛物线上，D、E在x轴上，CF交y轴于点B（0，2），且其面积为S。

⑴求抛物线的解析式。

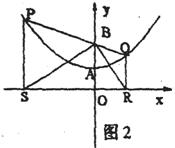
⑵如图⑵若点P为抛物线上不同于A的一点，连结PB并延长交抛物线于点Q，过点P、Q分别作x轴的垂线，垂足分别为S、R。

①　  求证：PB=PS

②判断△SBR的形状；

③试探索在线段SR上，是否存在点M，使得以点P、S、M为顶点的三角形和以Q、R、M为顶点的三角形相似，若存在，请求M点的位置；若不存在说明理由。