初三数学试题
| 题次 | 一 | 二 | 三 | 四 | 五 | 六 | 总分 | ||||||
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||||
| 得分 | |||||||||||||
一、选择题。每小题给出四个供选答案中，只有一个正确，把你认为正确的答案代号填在下表相应题号的空格内（4分×10＝40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1、
用配方法解方程
此方程可变形为（ ）
A、 
B、
C、
D、
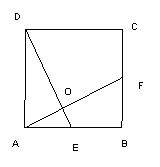2、如图，正方形ABCD中，E、F分别是AB、BC的中点，AG与DF相交于点O，则
＝（ ）
A、 
B、 
C、 
D、 
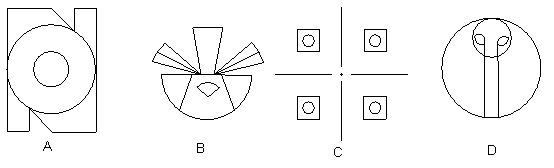
3、下列图形既是中心对称又是轴对称图形的是（ ）
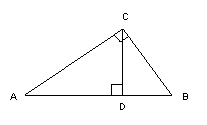
4、如图，在Rt△ABC中，∠C＝90
，CD⊥AB于点D，已知AC＝
，BC＝2，那么
∠ACD＝（ ）
A、 
B、 C、
D、
5、一个几何体是由一些小正方体摆成，其主（正）视图与左视图（如图所示）其府视图不可能是选项中的（ ）
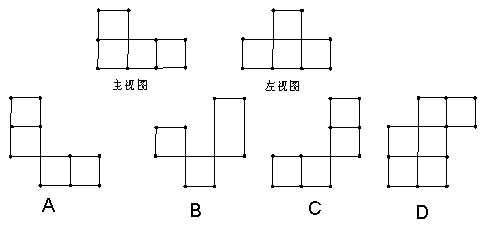
6、打开某洗衣机开关，在洗涤衣服时（洗衣机内无水）洗衣机经历了进，清水，排水，脱水四个连续过程，其中进，清洗，排水时洗衣机的水量
与时间
之间满足某种函数关系，其函数图象大致为（ ）
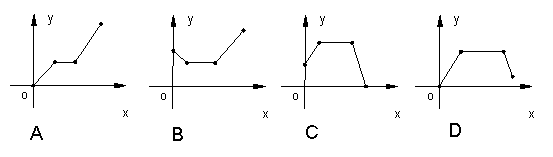7、如图、在直线m上摆放着三个正三角形，△ABC，△HFG，△DCE，已知BC＝CE，F、G分是BC、CE的中点，FM∥AC，GN∥DC，设图中三个平行四边形的面积依次是S1、S2、S3、若 则S2＝（ ）
A、 2 B、 4 C、 3 D、 6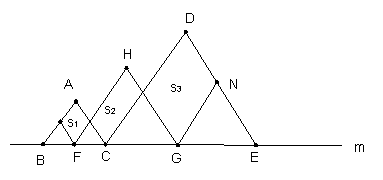 
8、如图，为了保持原图案的模式，应在空白处补上（ ）
A、
B、
C、
D、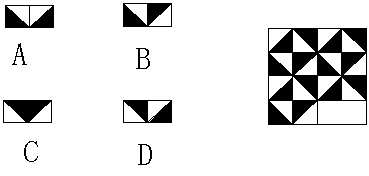 
9、函数
的像，如图所示，所给出以下结论
其中正确是结论（ ）
A、 ③④ B、②③ C、①④ D、 ①②④
10、如图所示的国旗，旗杆在一天中四个不同时刻的影子，请你将四幅图按先后顺序排到的是（ ）
A、①③④② B、④①③②
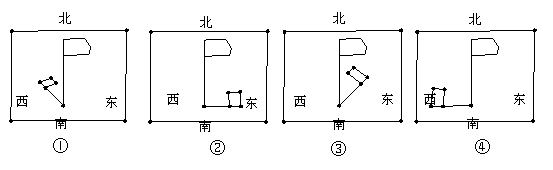
C、③①②④ D、④②①③
二、填空题。（每小题4分，共20分）
11、若
则
的值为__________________
12、从100张分别写上1－100的数字卡片中，随意抽取一张是7的倍数的概率是__________________
13、已知二次函数
的图像过点A（c，0），且关天直线
＝2 对称，则这个二次函数的解析式可能是__________________（只要求写出一个可能的解析式）
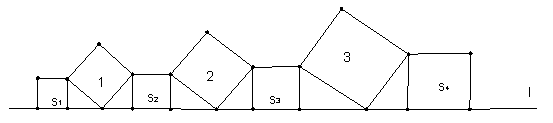
14、在直线
上依次摆放着七个正方形（如图），已知斜入置的三个正方形的面积分别1、2、3，正放置的四个正方形的面积分别S1、S2、S3。则
＝__________________
15、计算
＝_______________
三解答下列各题（共3小题，每小题8分共24分）
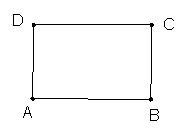
16、若一个矩形的短边与长边的比值为
（黄金分割数），我们把这样的矩形叫做黄金矩形
（1）操作，请你在如图所示的黄金矩形ABCD（AB＞AD）中，以短边AD为一边作正方形AEFD
（2）探究：在（1）中四边形EBCF是不是黄金矩形？若是请给予证明，若不是，请说明理由。
（3）归纳：通过上述操作及探究，请概括出具有一般性的结论（不需要证明）
 |
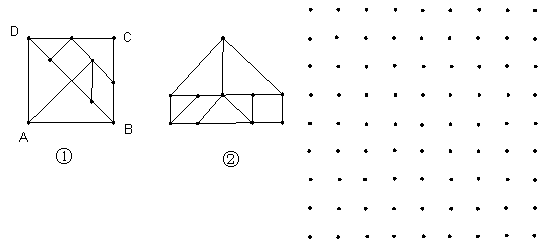
17、对正方形ABCD的分划如图①其中E、F分别是BC，CD的中点，M、N、G分别是OB、OD、EF的中点，沿分划线可以剪出一副由七块部件组成的“七巧板”
（1）如果设正方形OGFN的边长为1，这七快部件的各边边长中，从小到大的四个不同值分别为1，
那么
＝__________________各内角中最小内角是__________________度，最大内角是________________度，用它们拼成的一个五边形如图②，其中面积为__________________。
（2）请用这副七巧，既不留下一丝空白，又不相互重叠，拼出2种边数不同的凸多边形，画在下面格点图中，并使凸多边形的顶点落在格点图的小黑点上（格点图中，上下，左右相邻两点距都为1）
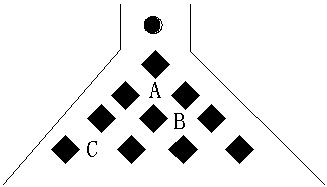
18、在科技馆里，小亮看见一台名为帕斯卡三角的仪器，如图所示，当一实心小球从入口落下，它依次碰到每层菱形挡快时，会等可能地向左或向右落下，（1）小球通过第二层A位置的概率是多少？
（2）请用学过的数学方法模拟该试验。并具体说明小球下落到第三层B位置和第四层C位置处的概率各是多少？
四、解答题（每小题8分共16分）
19．读诗词解题（通过列方程式，算出周瑜去世的年龄）
大江东去浪淘尽，千古风流数人物，而立之年督东吴，早年英逝两位数。十位恰小个位三，个位平方与寿符，哪位学子算得快，多少年华属周喻？
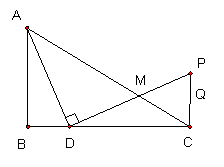
20、如图△ABC中，B＝90，∠BAD＝∠ACB，AB＝2，BD＝1过D作DM⊥AD交AC天点M，DM的延长线与点C的垂线交于点P。
（1）求∠ACB的值
（2）求MC的长
（3）若点Q以每秒1个单位的速度由点C向点P运动，是否存在某在某一时刻t，使四边形ADQP的面积等于四边形ABCQ的面积，若存在，求出t的值，若不存在，请说明理由。
 |
五、解答题。（每小题10分共30分）
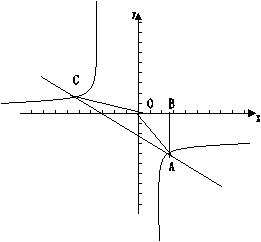
21、如图，在Rt△ABO的顶点是双曲线
与直线
在第四象限的交点。AB垂直轴于点B。且
＝
（1） 求这两个函数的解析式
（2） 求直线与双曲线的两个交点A、C的坐标和△AOC的面积。
 |
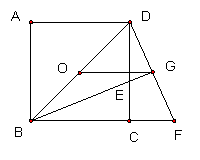
22、已知：如图，O是正方形ABCD的中心，BE平分∠DBC，交DC于点E，延长BC到点F，使CF＝CE，连接DF交BE的延长线于点G，连接OG
①求证△BCE≌△DCF
②OG与BF有什么关系？证明的结论。
③若GE·GB＝4－
。求正方形ABCD的面积。
 |
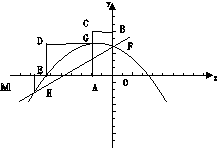
23、如图O点是坐标原点，点A（n,0）是轴上一动点，（n0）以AO为一边作矩形AOBC，使OB＝2OA，点C在第二象限，将矩形AOBC绕点A逆时针旋转90，得矩形AGDE，过点A的直线
交
轴于点F，FB＝FA，抛物线
过点E、F、G，且和直线AF交于点H，过点H作轴的垂线，垂足为点M，
（1）求
的值
（2）点A位置改变时△AMH的面积和矩形AOBC的面积比是否改变？说明你的理由。
 |
六、解答题（每小题10分共20分）
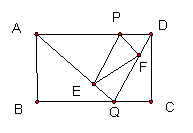
24、如图，已知矩形ABCD的边长AB＝2，BC＝3。点P是AD边上的一动点（点P异于A、D）Q是BC边上任意一点，连接AQ，DQ，过点P作PE∥DQ交于AQ于点E，作PF ∥AQ交DQ于点F。
（1）求证△APE∽△ADQ
（2）AP的长为，试求△PEF的面积关于的函数关系式，并求当P在何处时
取得最大值？最大值是多少？
（3）当Q在何处时△ADQ的周长最小？（需给出确定Q在何处的过程或方法但不必给证明）
 |
25、如图①，以矩形OABC的两边OA和OC所在的直线为轴，轴建立平面直角坐标系，A点坐标为（3，0），C点坐标为（0，4），将矩形OABC绕O点逆时针旋转，使B点落在 轴的正半轴上，旋转后的矩形为OA1，B1C1，BC，A1B1相交于点M，
（1）求点B1的坐标与线段B1C的长。
（2）将图①中的矩形OA1B1C1沿 轴向上平移，如图②，矩形PA2B2C2是平移过程中的某一位置，BC、A2B2相交于点M1，点P运动到C点停止，设点P运动的距离为 ，矩形PA2B2C2与原矩形OABC重叠部分的面积为 求关于 的函数关系式，并写出 的取值范围。
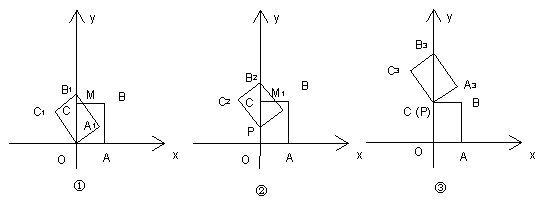（3）如图③，当点P运动到C时，平移后的矩形PA3B3C3请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的作法。