2003年太仓高级中学理科实验班提前招生考试试卷
（数学部分）
考试时间：2003年12月20日上午
一、选择题（每小题4，共24分）
1、用去分母方法解分式方程
，产生增根，则m的值为（ ）
A、--1或—2 B、--1或2 C、1或2 D、1或—2
2、关于x的方程
有实数根α、β，则α+β的取值范围为（ ）
A、α+β≤1 B、α+β≥1 C、α+β≥
D、α+β≤
3、已知PT切⊙O于T，PB为经过圆心的割线交⊙O于点A，（PB>PA），若PT=4，PA=2，则cos∠BPT=（ ）
A、
B、
C、
D、
4、矩形ABCD中，AB=3，AD=4，P为AD上的动点，PE⊥AC垂足为E，PF⊥BD垂足为F，则PE+PF的值为（ ）
A、
B、2 C、
D、
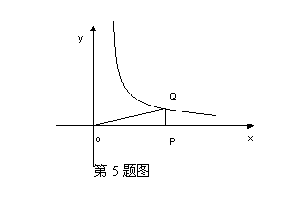
5、如图P为x轴正半轴上一动点，过P作x轴的垂线PQ交双曲线
于点Q，连接OQ，当P沿x轴正方向运动时，Rt△QOP的面积（ ）
A、逐渐增大 B、逐渐减小 C、保持不变 D、无法确定
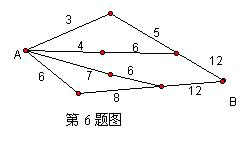6、如图小圆圈表示网络的结点，结点之间的连线表示它们有网线相连，连线标明的数字表示该段网线单位时间内通过的最大信息量，现从结点A向结点B传递信息，信息可以分开沿不同的线路同时传递，则单位时间内传递的最大信息量为（ ）
A、26 B、24 C、20 D、19
二、填空题（每小题4分，共36分）
7、若a、b、c 满足等式
，则
=
8、若
，
，则代数式
的值为
9、方程
的解为
10、若点M（1--x，1--y）在第二象限，那么点N（1—x¸ y—1）关于原点对称点P在第 象限。
11、若m、n是关于x的方程
的两个实数根，则代数式
的值为
12、已知方程
的两根都比5大，则实数k的范围是
13、2003年世界女排锦标赛上，中国女排以11战全胜获得冠军，在这次锦标赛上共有12支球队，采用单循环制（即每两个球队打一场），则主办单位共安排了 场比赛。
14、如图：⊙O内切于边长为2的等边△ABC，分别以A、B、C为圆心，1为半径画弧，则图中阴影部分面积为
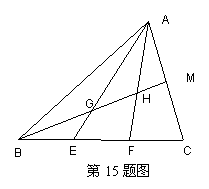
15、如图△ABC中，E、F为BC的三等份点，M为AC的中点，BM与AE、AF分别交于G、H，则BG：GH：HM=
三、计算题（本大题40分）
16、（本题12分）某广告公司设计一幅周长为12米的矩形广告牌，广告设计费为每平方米1000元，设矩形的一边长为x 米，面积为S平方米。（1）求S与x之间的函数关系式，并确定自变量x的取值范围；（2）请你设计一个方案，使获得的设计费最多，并求出这个费用；（3）为使广告牌美观、大方，要求做成黄金矩形，请你按要求设计，并计算出可获得的设计费是多少？（精确到元）（参考资料：①当矩形的长是宽与（长+宽）的比例中项时，这样的矩形叫做黄金矩形；②
）
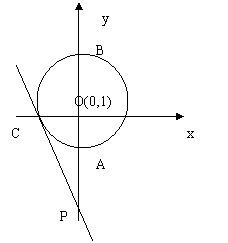17、（本题12分）已知如图⊙D交y轴于AB，交x轴于点C，过点C的直线：
与y轴交P；（1）证明：PC是⊙D的切线；（2）判断在直线PC上是否存在点E，使得
，若存在求出点E的坐标，若不存在，请说明理由；
（3）当直线PC绕点P转动时，与劣弧
交于点F（不与A、C重合），连结OF，设PF=m，OF=n，求m、n之间满足的函数关系式，并写出自变量n的取值范围。
五、阅读、理解、应用
18、（本题16分）
~36间的角的三角函数
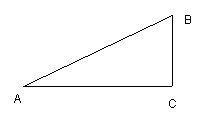
在初中，我们学习过锐角的正弦、余弦、正切和余切四种三角函数，即在图1所示的直角三角形ABC，∠A是锐角，那么
sinA=
，cosA=
，tanA=
，cotA=
|
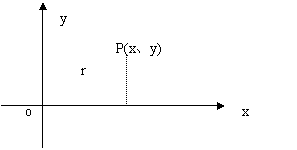
为了研究需要，我们再从另一个角度来规定一个角的三角函数的意义：
设有一个角α，我们以它的顶点作为原点，以它的始边作为x轴的正半轴ox，建立直角坐标系（图2），在角α的终边上任取一点P，它的横坐标是x，纵坐标是y ，点P 和原点（0，0）的距离为
（r总是正的），然后把角α的三角函数规定为：
sinα=
，cosα=
，tanα=
，cotα=
我们知道，图1的四个比值的大小与角A的大小有关，而与直角三角形的大小无关，同样图2中四个比值的大小也仅与角α的大小有关，而与点P在角α的终边位置无关.
比较图1与图2，可以看出一个角的三角函数的意义的两种规定实际上是一样的，根据第二种定义回答下列问题，每题4分，共16分
1．若27<α<36，则角α的三角函数值sinα、cosα、tanα、cotα，其中取正值的是
2．若角α的终边与直线y=2x 重合，则sinα+ cosα=
3．若角α是钝角，其终边上一点P（x，
），且cosα=
，则tanα
4．若
≤α≤9 ，则 sinα+cosα 的取值范围是