2006年提前批数学模拟（三）
命题人： 沈小兵 2006、4
一、选择题（共5小题，每小题6分，满分30分. 以下每道小题均给出了代号为A，B，C，D的四个选项，其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里. 不填、多填或错填得零分）
1．方程
的所有整数解的个数是（ ）
（A）2个 （B）3个 （C）4个 （D）5个
2. 若直角三角形的两条直角边长为
、
，斜边长为
，斜边上的高为
，则有 （
）.
（A）
（B）
（C）
（D）
3．一条抛物线
的顶点为（4，
），且与x轴的两个交点的横坐标为一正一负，则a、b、c中为正数的（
）.
（A）只有
（B）只有
（C）只有 （D）只有和
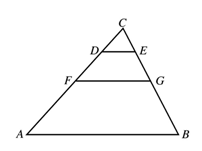4．如图所示，在△ABC中，DE∥AB∥FG，且FG到DE、AB的距离之比为1:2. 若△ABC的面积为32，△CDE的面积为2，则△CFG的面积S等于
（ ）.
（A）6 （B）8
（C）10 （D）12
5．如果x和y是非零实数，使得
和
那么x+y等于（ ）.
（A）3 （B）
（C）
（D）
二、填空题（共5小题，每小题6分，满分30分）
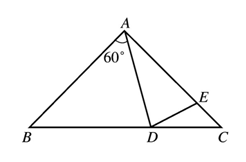
6． 如图所示，在△ABC中，AB=AC，AD=AE，
，则
（度）.
7．据有关资料统计，两个城市之间每天的电话通话次数T与这两个城市的人口数m、n（单位：万人）以及两城市间的距离d（单位：km）有
的关系(k为常数) . 现测得A、B、C三个城市的人口及它们之间的距离如图所示，且已知A、B两个城市间每天的电话通话次数为t，那么B、C两个城市间每天的电话通话次数为
次（用t表示）.
8、已知不等式
≥0的正整数解为1，2，3，则的取值范围是
．
9．如果对于任意两个实数、，“
”为一种运算，定义为
，则函数
（－3≤
≤3）的最大值与最小值的和为
．
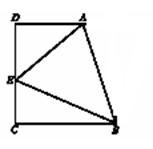
10． 如图所示，在梯形ABCD中，AD∥BC
(BC>AD)，
，BC=CD=12, 
，若AE=10，则CE的长为 .
三、解答题（共4题，每小题15分，满分60分）
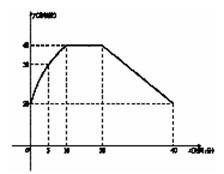11．通过实验研究，专家们发现：初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的，讲课开始时，学生的兴趣激增，中间有一段时间，学生的兴趣保持平稳的状态，随后开始分散. 学生注意力指标数y随时间x（分钟）变化的函数图象如图所示（y越大表示学生注意力越集中）. 当
时，图象是抛物线的一部分，当
和
时，图象是线段.
（1）当时，求注意力指标数y与时间x的函数关系式；
（2）一道数学竞赛题需要讲解24分钟. 问老师能否经过适当安排，使学生在听这道题时，注意力的指标数都不低于36.
12．预计用1500元购买甲商品个，乙商品
个，不料甲商品每个涨价1.5元，乙商品每个涨价1元，尽管购买甲商品的个数比预定数减少10个，总金额仍多用29元．又若甲商品每个只涨价1元，并且购买甲商品的数量只比预定数少5个，那么甲、乙两商品支付的总金额是1563.5元．
（1）求、的关系式；
（2）若预计购买甲商品的个数的2倍与预计购买乙商品的个数的和大于205，但小于210，求、的值．
13．如图，形如量角器的半圆O的直径DE=12cm，形如三角板的⊿ABC中，
∠ACB=90°，∠ABC=30°，BC=12cm。半圆O以2cm/s的速度从左向右运动，在运动过程中，点D、E始终在直线BC上。设运动时间为t (s)，当t=0s时，半圆O在⊿ABC的左侧，OC=8cm。
（1） 当t为何值时，⊿ABC的一边所在直线与半圆O所在的圆相切？
（2） 
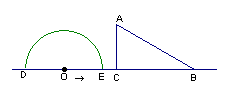当⊿ABC的一边所在直线与半圆O所在的圆相切时，如果半圆O与直线DE围成的区域与⊿ABC三边围成的区域有重叠部分，求重叠部分的面积。