一、选择题
1、(2005泉州课该实验区) 如图,⊙O为△ABC的外接圆,直径AB=10,弦BC=8,则弦AC=
.
如图,⊙O为△ABC的外接圆,直径AB=10,弦BC=8,则弦AC=
.
2、
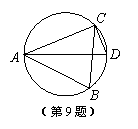 1、(南通2005)9. 如图,已知AD是△ABC的外接圆的直径,AD =13 cm,
1、(南通2005)9. 如图,已知AD是△ABC的外接圆的直径,AD =13 cm,![]() ,则AC的长等于D
,则AC的长等于D
A.5 cm B.6 cm
C.10 cm D.12 cm
2、(2005福建福州)9、一个底面半径为5cm,母线长为16cm的圆锥,它的侧面展开图的面积是……( A )
A、80πcm2 B、40πcm2 C、80cm2 D、40cm2
3、 (2004河北实验区)如图5,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,
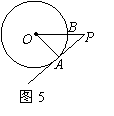 OA=3,则cos∠APO的值为( C )
OA=3,则cos∠APO的值为( C )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 10.(2005安徽课该实验区) 如图, ⊙O的半径OA=6, 以A为圆心,OA为半径的弧叫⊙O于B、C点, 则BC= ( )
10.(2005安徽课该实验区) 如图, ⊙O的半径OA=6, 以A为圆心,OA为半径的弧叫⊙O于B、C点, 则BC= ( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
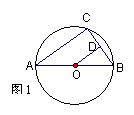
9.(20005广东佛山市课改实验区) 如图1,AB是⊙O的直径,C是⊙O上一点,若AC︰BC=![]() ︰
︰![]() ,AB=10
,AB=10![]() ,OD⊥BC于点D,则BD的长为(
B ).
,OD⊥BC于点D,则BD的长为(
B ).
 A.
A.![]() B.3
B.3![]() C.5
C.5![]() D.6
D.6![]()
8、(2005广东茂名课该实验区)如图,梯形ABCD内接于◎○,AB//CD,AB为直径,DO平分∠ADC,则∠DAO的度数是(D)
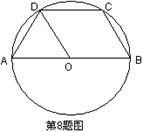 A、900, B、800, C、700, D、600;
A、900, B、800, C、700, D、600;
9、(2005广东茂名课该实验区)下列三个命题:
① 园既是轴对称图形,又是中心对称图形;
② 垂直于弦的直径平分这条弦;
③ 相等圆心角所对的弧相等;
其中是真命题的是(A)
A、①② ,B、②③ ,C、①③ ,D、①②③;
 7.(2005湖北省十堰石课改实验区)已知⊙
7.(2005湖北省十堰石课改实验区)已知⊙![]() 和⊙
和⊙![]() 的半径分别为2cm和3cm,两圆的圆心距是5cm,则两圆的位置关系是(D)
的半径分别为2cm和3cm,两圆的圆心距是5cm,则两圆的位置关系是(D)
A、相交 B、外离 C、内切 D、外切
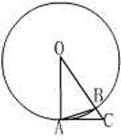
8.如图,A、B是⊙O上的两点,AC是⊙O的切线,∠OBA=75°,
⊙O的半径为1,则OC的长等于(C)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
 4.(2005山东大连课改实验区)已知两圆的半径分别为1和4,圆心距为3,则两圆的位置关系是( D )
4.(2005山东大连课改实验区)已知两圆的半径分别为1和4,圆心距为3,则两圆的位置关系是( D )
A、外离 B、外切 C、相交 D、内切
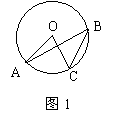
7.(2005山东大连课改实验区)如图1,A、C、B是⊙O上三点,若∠AOC=40°,则∠ABC的度数是( B )
A、10° B、20° C、40° D、80°
 二、填空题:
二、填空题:
13.(2005山东大连课改实验区)如图3,AB是⊙O的直径,AC是⊙O的切线,且AB=AC,则∠C的度数是__45°____。
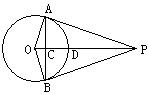 3、(2004灵武·开福·曲沃·乌海实验区卷)如图,P是⊙O外一点,OP垂直于弦AB于点C,交
3、(2004灵武·开福·曲沃·乌海实验区卷)如图,P是⊙O外一点,OP垂直于弦AB于点C,交![]() 于点D,连结OA、OB、AP、BP。根据以上条件,写出三个正确结论(OA=OB除外):
于点D,连结OA、OB、AP、BP。根据以上条件,写出三个正确结论(OA=OB除外):
①
;②
;③
。
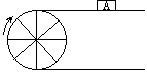 4、(2004灵武·开福·曲沃·乌海实验区卷)如图,当半径为30cm的转动轮转过120°角时,传送带上的物体A平移的距离为 cm。
4、(2004灵武·开福·曲沃·乌海实验区卷)如图,当半径为30cm的转动轮转过120°角时,传送带上的物体A平移的距离为 cm。
1、(2005福建福州)14、平面内半径分别为3和2的两圆内切,则这两圆的圆心距等于_______
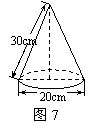
13. 图7是小明制作的一个圆锥形纸帽的示意图.围成这个纸帽
的纸的面积为 cm2(π取3.14).
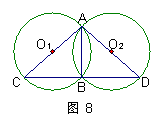
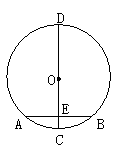 15、“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”此问题的实质就是解决下面的问题:“如图8,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长”。根据题意可得CD的长为 26 。
15、“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”此问题的实质就是解决下面的问题:“如图8,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长”。根据题意可得CD的长为 26 。
16.(2005扬州)如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,
则∠APB= °

|
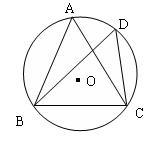
14、(2004深圳南山区课该实验区)如图10,在⊙O中,已知∠ACB=∠CDB=60°,AC=3,则△ABC的周长是 。
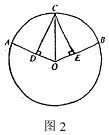
 6 (2004广西南宁课该实验区)如图2,D、E分别是⊙O的半径OA、OB上的点,CD⊥OA、CE⊥OB、CD=CE,则AC与CB两弧长的大小关系是:
.
6 (2004广西南宁课该实验区)如图2,D、E分别是⊙O的半径OA、OB上的点,CD⊥OA、CE⊥OB、CD=CE,则AC与CB两弧长的大小关系是:
.
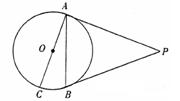
 10、(2005广东课改实验区)如图,PA、PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠BAC=°20,则P的大小是 40 度。
10、(2005广东课改实验区)如图,PA、PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠BAC=°20,则P的大小是 40 度。
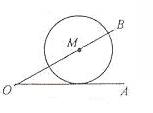
14.已知∠AOB=30°,M为OB边上任一点,以M为圆心,2cm
为半径坐⊙M,当OM= cm时,⊙M与OA相切(如图)
13、(2005河南课改实验区)如图,在⊙O中,弦AB=AC=5cm,BC=8cm,则⊙O的半径等于 ![]() cm。
cm。
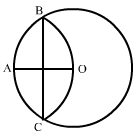
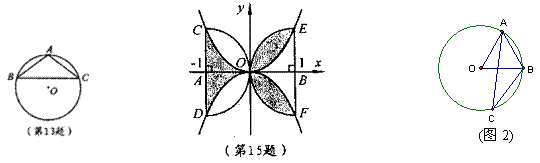 15、(2005河南课改实验区)如图,半圆A和半圆B均与y轴相切于点O,其直径CD、EF均和x轴垂直,以O为顶点的两条抛物线分别经过点C、E和点D、F,则图中阴影部分的面积是
15、(2005河南课改实验区)如图,半圆A和半圆B均与y轴相切于点O,其直径CD、EF均和x轴垂直,以O为顶点的两条抛物线分别经过点C、E和点D、F,则图中阴影部分的面积是 ![]() 。
。
8.(2005江苏徐州课改实验区)如图2,A、B、C是⊙O上的点,AB = 2㎝,∠ACB=30°,那么⊙O的半径为___________________.
三、解答题
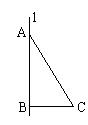 1、(2005福建漳州)22.如图:已知在Rt△ABC中,∠ABC=90°,∠C=60°,边AB=6cm.
1、(2005福建漳州)22.如图:已知在Rt△ABC中,∠ABC=90°,∠C=60°,边AB=6cm.
(1) 求边AC和BC的值;
(2) 求以直角边AB所在的直线l为轴旋转一周所得的几何体的侧面积.
(结果用含π的代数式表示)
2、(2005福建)22.解:(1)AC=![]() cm,BC=
cm,BC=![]() cm
cm
 (2)所求几何体的侧面积S=
(2)所求几何体的侧面积S=![]() (
(![]() )
)
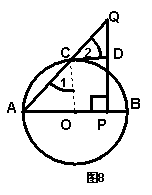
20、已知:如图8,AB是⊙O的直径,P是AB上的一点(与A、B不重合),QP⊥AB,垂足为P,直线QA交⊙O于C点,过C点作⊙O的切线交直线QP于点D。则△CDQ是等腰三角形。对上述命题证明如下:
证明:连结OC
∵OA=OC
∴∠A=∠1
∵CD切O于C点
∴∠OCD=90°
 ∴∠1+∠2=90°
∴∠1+∠2=90°
∴∠A+∠2=90°
在RtQPA中,QPA=90°
∴∠A+∠Q=90°
∴∠2=∠Q
∴DQ=DC
即CDQ是等腰三角形。
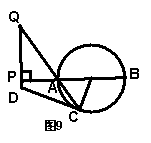
问题:对上述命题,当点P在BA的延长线上时,其他条件不变,如图9所示,结论“△CDQ是等腰三角形”还成立吗?若成立,误给予证明;若不成立,请说明理由。
20、答:结论“△CDQ是等腰三角形”还成立
证明:略
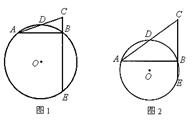
3、(2005北京) (本题满分8分) 24. 已知:在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A、D、B三点,CB的延长线交⊙O于点E(如图1)。
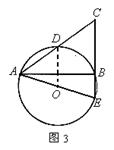
在满足上述条件的情况下,当∠CAB的大小变化时,图形也随着改变(如图2),在这个变化过程中,有些线段总保持着相等的关系。
(1)观察上述图形,连结图2中已标明字母的某两点,得到一条新线段,证明它与线段CE相等;
(2)在图2中,过点E作⊙O的切线,交AC的延长线于点F。
①若CF=CD,求sin∠CAB的值;
②若![]() ,试用含n的代数式表示sin∠CAB(直接写出结果)。
,试用含n的代数式表示sin∠CAB(直接写出结果)。
(1)连结__________________
求证:_________=CE
 证明:
证明:
(2)解:①
②![]() _____________(
_____________(![]() )
)
(1)连结AE
求证:AE=CE
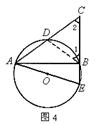 证法一:如图3,连结OD ∵∠ABC=90°,CB的延长线交⊙O于点E ∴∠ABE=90° ∴AE是⊙O的直径
证法一:如图3,连结OD ∵∠ABC=90°,CB的延长线交⊙O于点E ∴∠ABE=90° ∴AE是⊙O的直径
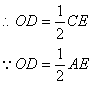 ∵D是AC的中点,O是AE的中点
∵D是AC的中点,O是AE的中点
 ∴AE=CE
∴AE=CE
证法二:如图4,连结BD 在Rt△ABC中,∠ABC=90°∵D是AC的中点 ∴AD=CD=BD ∴∠1=∠2 ∵四边形AEBD内接于⊙O ∴∠1=∠DAE
∴∠2=∠DAE ∴AE=CE
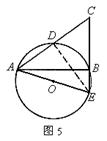
证法三:如图5,连结DE
 同证法一,得AE是⊙O的直径 ∴∠ADE=90°
∵D是AC的中点 ∴DE是线段AC的垂直平分线 ∴AE=CE
同证法一,得AE是⊙O的直径 ∴∠ADE=90°
∵D是AC的中点 ∴DE是线段AC的垂直平分线 ∴AE=CE
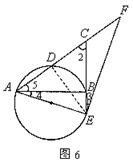
(2)①解法一:根据题意画出图形,如图6,连结DE。 ∵EF是⊙O的切线
∴∠3=∠4,且![]()
![]() 设
设![]() ,则
,则![]()
![]()
 ∵AE是⊙O的直径 ∴∠AEF=90° 在Rt△AEF中,
∵AE是⊙O的直径 ∴∠AEF=90° 在Rt△AEF中,![]()
![]()
![]()
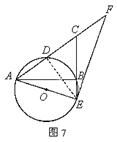
解法二:根据题意画出图形,如图7,连结DE。
∵AE是⊙O的直径,EF是⊙O的切线 ∴∠ADE=∠AEF=90° ∴Rt△ADE∽Rt△EDF ![]()
设![]() ,则
,则![]()
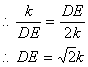 在Rt△CDE中
在Rt△CDE中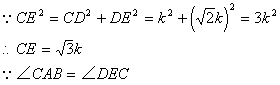
![]()
②![]() (
(![]() )
)
22*( 2005年恩施自治州课改实验区)在探讨圆周角与圆心角的大小关系时,小亮首先考虑了一种特殊情况(圆心在圆周角的一边上)如图(1)所示:
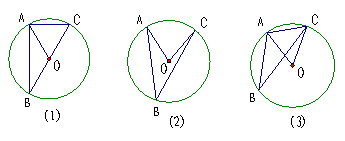 ∵∠AOC是⊿ABO的外角
∵∠AOC是⊿ABO的外角
∴∠AOC=∠ABO+∠BAO
又∵OA=OB
∴∠OAB=∠OBA ∴∠AOC=2∠ABO
即∠ABC=![]() ∠AOC
∠AOC
 如果∠ABC的两边都不经过圆心,如图(2)、(3),那么结论会怎样?请你说明理由.
如果∠ABC的两边都不经过圆心,如图(2)、(3),那么结论会怎样?请你说明理由.
 | |||
22. 如果∠ABC的两边都不经过圆心,
结论∠ABC=![]() ∠AOC仍然成立 ( 2分)
∠AOC仍然成立 ( 2分)
(1)对图2的情况
连接BO并延长交圆O于点D ( 3分)
由图1知:
∠ABD=![]() ∠AOD
∠AOD
∠CBD=![]() ∠COD
( 5分)
∠COD
( 5分)
∴∠ABD+∠CBD=![]() ∠AOD+
∠AOD+![]() ∠COD
∠COD
即∠ABC=![]() ∠AOC
( 8分)
∠AOC
( 8分)
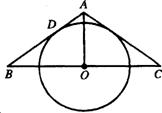 (2) 对图3的情况仿图2的情况可证 ( 10分)
(2) 对图3的情况仿图2的情况可证 ( 10分)
24.(2005甘肃省课改实验区)(10分)如图lO,AO是△ABC的中线,⊙D与AB边相切于点D.
(1)要使⊙O与AC边也相切,应增加条件 .(任写一个)
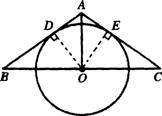 (2)增加条件后,请你证明⊙O与AC边相切.
(2)增加条件后,请你证明⊙O与AC边相切.
24.(1)答案不唯一.
(2)增加条件∠B=∠C后,⊙O与AC边相切.
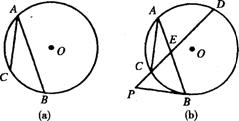
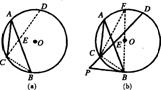
28.(2005甘肃省课改实验区)(1 0分)如图1 3,已知AC、AB是⊙O的弦,AB>AC.
(1)在图l 3(a)中,能否在AB上确定一点E,使得AC2=AE·AB,为什么?
(2)在图1 3(b)中,在条件(1)的结沦下延长EC到P,连结PB,如果PB=PE,试判断PB和⊙O的位置关系,并说明理由.
 28.(1)作法有多种:
28.(1)作法有多种:
(2)如图(6),过点B作直径BF,连结CF.
29.(2005甘肃省课改实验区)(14分)如图14,已知两点A(-1,0)、B(4,O)在x轴上,以AB为直径的半圆P交y轴于点C.
(1)求经过A、B、C三点的抛物线的解析式;
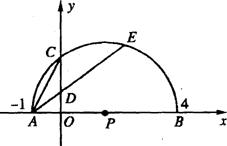 (2)设AC的垂直平分线交OC于D,连结AD并延长AD交半圆P于点E,︵AC与︵CE相等吗?请证明你的结论;
(2)设AC的垂直平分线交OC于D,连结AD并延长AD交半圆P于点E,︵AC与︵CE相等吗?请证明你的结论;
(3)设点M为x轴负半轴上一点,OM=![]() AE ,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在,请说明理由.
AE ,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在,请说明理由.
29.(1)∴点C的坐标是(O,2).
根据A(-1,0)、B(4,0),
设抛物线的解析式为y=a(x+1)(x-4).
y=![]() x2+
x2+![]() +2.
+2.
(2)弧AC=弧CE.
(3)不存在符合要求的直线.理由是:连结BE.设AD=x,
在Rt△AOD中,AD2=OA2+OD2,
解得x=5/4
∵△AOD∽△AEB,
OM=2.
∴点M的坐标为(-2,0).设过点M的直线对应函数的解析式为y=kx+b.
把点M(-2,0)代入,得b=2k_ ∴y=kx+2k. ①
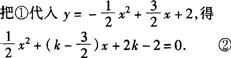
由题意知,方程②的两个根互为相反数,k=3/2.这时方程②无实数根,不存在符合要求的直线.
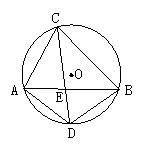
21.(2005宁夏课改实验区)
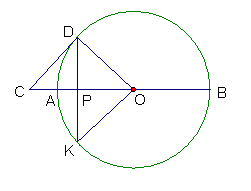 已知: 在⊙O中,CD平分∠ACB,弦AB、CD相交于点E,连结AD、BD.
已知: 在⊙O中,CD平分∠ACB,弦AB、CD相交于点E,连结AD、BD.
(1) 写出图中3对相似的三角形;
(2) 找出图中相等的线段,并说出理由.
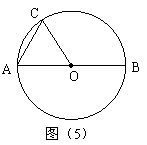
24、(2005四川课改实验区)如图,P是⊙O的半径OA上的一点,D在⊙O上,且PD=PO.过点D作⊙O的切线交OA的延长线于点C,延长DP交⊙O于K,连接KO,OD.
(1)证明:PC=PD;
(2)若该圆半径为5,CD∥KO,请求出OC的长.
27、(济南课改实验区)(本题9分)如图⑴,已知⊙O是等边△ABC的外接圆,过点O作MN∥BC分别交AB、AC于M、N,且MN=a。另一个与△ABC全等的等边△DEF的顶点D在MN上移动(不与点M、N重合),并始终保持EF∥BC,DF交AB于点P,DE交AC于点Q。
①试判断四边形APDQ的形状,并进行证明;
②设DM为x,四边形APDQ的面积为y,试探索y与x的函数关系式;四边形APDQ的面积能取到最大值吗?如果能,请求出它的最大值,并确定此时D点的位置;
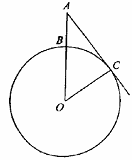 ③如图⑵,当D点和圆心O重合时,请判断四边形APDQ的形状,并说明理由;你能发现四边形APDQ的面积与△ABC的面积有何关系吗?为什么?
③如图⑵,当D点和圆心O重合时,请判断四边形APDQ的形状,并说明理由;你能发现四边形APDQ的面积与△ABC的面积有何关系吗?为什么?
 |  | ||
 23(2004广西南宁实验区)如图8,已知⊙O半径为8cm,点A为半径OB延长线上一点,射线AC切⊙O于点)C,BC弧的长为209πcm,求线段AB的长(精确到0.01cm).
23(2004广西南宁实验区)如图8,已知⊙O半径为8cm,点A为半径OB延长线上一点,射线AC切⊙O于点)C,BC弧的长为209πcm,求线段AB的长(精确到0.01cm).
25. (2004青海湟中实验区)(本题满分8分)如图(5),在⊙O中,AB是直径,半径为R,![]()
求:(1)∠AOC的度数.
(2)若D为劣弧BC上的一动点,且弦AD与半径OC交于E点.试探求△AEC≌△DEO时,D点的位置.
答案: (1)∠AOC=60° (2)D的位置,只要满足∠DOB=60°,或AC∥OD或劣弧BC的中点其中一条.
20、20-1(2005宜昌课该实验区).如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC交⊙O与点F.
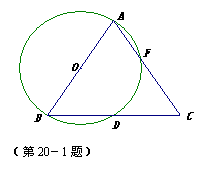 (1)AB与AC的大小有什么关系?为什么?
(1)AB与AC的大小有什么关系?为什么?
(2)按角的大小分类, 请你判断△ABC属于哪一类三角形,并说明理由.
2.小明按下面的方法作出了∠MON的平分线:
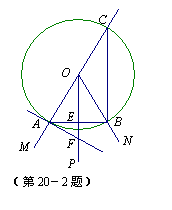 ①反向延长射线OM;
①反向延长射线OM;
②以点O为圆心,任意长为半径作圆,分别交∠MON的两边于点A、B,交射线OM的反向延长线于点C;
③连接CB;
④以O为顶点,OA为一边作∠AOP=∠OCB.
(1)根据上述作图,射线OP是∠MON的平分线吗?并说明理由
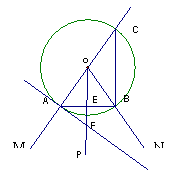
(2)若过点A作⊙O的切线交射线OP于点F,连接AB交OP于点E,当∠MON=60°、OF=10时,求AE的长.
 20—1.解:(1)(方法1)连接DO.∵OD是△ABC的中位线, ∴DO∥CA.∵∠ODB=∠C,∴OD=BO ∴∠OBD=∠ODB,∴∠OBD=∠ACB, ∴AB=AC
20—1.解:(1)(方法1)连接DO.∵OD是△ABC的中位线, ∴DO∥CA.∵∠ODB=∠C,∴OD=BO ∴∠OBD=∠ODB,∴∠OBD=∠ACB, ∴AB=AC
(方法2)连接AD, ∵AB是⊙O的直径,∴AO⊥BC,
∵BD=CD,∴AB=AC.
(方法3)连接DO.∵OD是△ABC的中位线,∴OD=![]() AC
AC
OB=OD=![]() AB ∴AB=AC
AB ∴AB=AC
(2) 连接AD,∵AB是⊙O的直径,∴∠ADB=90°
∴∠B<∠ACB=90°.∠C<∠ACB=90°.∴∠B、∠C为锐角.
∵AC和⊙O交于点F,连接BF,
∴∠A<∠BFC=90°.∴△ABC为锐角三角形
20-2. 解:(1)(方法一)∵∠AOF=∠OCB, 又∵∠BOA=2∠OCB,
∴∠AOF=∠BOF∴OP为∠BOA的角平分线
(方法二)∵∠AOF=∠OCB,∴PO∥BC ,∴∠POB=∠OBC,又∵OB=OC,
∴∠OCB=∠OBC,∴∠AOF=∠POB,∴OE为∠BOD的角平分线
(2)(方法一)∵AF与⊙O相切,∴AF⊥AO,
∵∠MON=60°,∴∠AOF=![]() ∠MON=30°,∴AF=
∠MON=30°,∴AF=![]() OF=5,由勾股定理得:AO=5
OF=5,由勾股定理得:AO=5![]() . ∵AO=BO,∴△AOB是等腰三角形,∵OP平分∠AOB,∴PO⊥AB,
. ∵AO=BO,∴△AOB是等腰三角形,∵OP平分∠AOB,∴PO⊥AB,
在Rt△AOF中,S⊿AOF=![]() AO×AF=
AO×AF=![]() FO×AE,即:5
FO×AE,即:5![]() ×5=10×AE,
×5=10×AE,
∴AE=![]() .
.
(方法二)∵∠MON=60°,∴⊿AOB为正三角形,∵OP平分∠MON,
∴AE=BE=![]() AB, ∵OP平分∠BOD,∴∠BOF=30°,又∵AF与⊙O相切,∴AF⊥AO
AB, ∵OP平分∠BOD,∴∠BOF=30°,又∵AF与⊙O相切,∴AF⊥AO
在Rt⊿AOF中,AO=5![]() , ∴AB=AO=5
, ∴AB=AO=5![]() ,∴AE=
,∴AE=![]()
22.(2005恩施自治州课改实验区)在探讨圆周角与圆心角的大小关系时,小亮首先考虑了一种特殊情况(圆心在圆周角的一边上)如图(1)所示:
 ∵∠AOC是⊿ABO的外角
∵∠AOC是⊿ABO的外角
∴∠AOC=∠ABO+∠BAO
又∵OA=OB
∴∠OAB=∠OBA ∴∠AOC=2∠ABO
即∠ABC=![]() ∠AOC
∠AOC
 如果∠ABC的两边都不经过圆心,如图(2)、(3),那么结论会怎样?请你说明理由.
如果∠ABC的两边都不经过圆心,如图(2)、(3),那么结论会怎样?请你说明理由.
 | |||
25.(2005福建厦门课改实验区) (本题满分12分) 已知:⊙O1与⊙O2相交于点A、B,过点B作CD⊥AB,分别交⊙O1和⊙O2于点C、D.
(1)如图8,求证:AC是⊙O1的直径;
(2)若AC=AD,
① 如图9,连结BO2、O1 O2,求证:四边形O1C BO2是平行四边形;
② 若点O1在⊙O2外,延长O2O1交⊙O1于点M,在劣弧︵MB上任取一点E(点E与点B不重合). EB的延长线交优弧︵BDA于点F,如图10所示. 连结 AE、AF.
则AE AB(请在横线上填上 “≥、≤、<、>”这四个不等号中的一个)并加以证明.
(友情提示:结论要填在答题卡相应的位置上)
 | 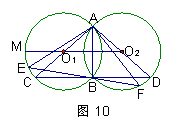 | ||||
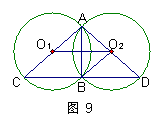 | |||||
 25. (本题满分12分)
25. (本题满分12分)
(1) 证明:∵ CD⊥AB …… 1分
∴∠ABC=90° …… 2分
∴ AC是⊙O1的直径 …… 3分
(2)
① 证明1:∵ CD⊥AB ∴∠ABD=90°
∴ AD是⊙O2的直径 …… 4分
∵ AC=AD
∵ CD⊥AB ∴CB=BD …… 5分
∵ O1、O2分别是AC、AD的中点
∴ O1O2∥CD且 O1O2=CD=CB …… 6分
 ∴ 四边形O1C BO2是平行四边形
…… 7分
∴ 四边形O1C BO2是平行四边形
…… 7分
证明2:∵ CD⊥AB ∴∠ABD=90°
∴ AD是⊙O2的直径 …… 4分
∵ AC=AD
∵ CD⊥AB ∴CB=BD …… 5分
∵ B、O2分别是CD、AD的中点
∴ BO2∥AC且 BO2=AC=O1C …… 6分
∴ 四边形O1C BO2是平行四边形 …… 7分
证明3:∵ CD⊥AB ∴∠ABD=90°
∴ AD是⊙O2的直径 …… 4分
∵ O1、O2分别是AC、AD的中点
∴ O1O2∥CD …… 5分
∵ CD⊥AB ∴ CB=BD
∴ B是CD的中点
∴O2B∥O1C …… 6分
∴四边形O1C BO2是平行四边形 …… 7分
证明4:∵ CD⊥AB ∴∠ABD=90°
∴ AD是⊙O2的直径 …… 4分
∵ AC=AD
∴ O1C=O2B
∴ ∠C=∠D ------------------------------------------------ 5分
∵ O2B=O2D
∴∠O2B D=∠D ……∴∠C=∠O2B D
∴O2B∥O1C …… 6分
 ∴四边形O1C
BO2是平行四边形
…… 7分
∴四边形O1C
BO2是平行四边形
…… 7分
② AE > AB …… 8分
证明1:当点E在劣弧︵MC上(不与点C重合)时,
∵ AC=AD
∴ ∠ACD=∠ADC
∴ ∠AEB=∠ACD=∠ADC=∠AFB
∴ AE=AF …… 9分
记AF交BD为G ∵ AB⊥CD
∴ AF>AG>AB …… 10分
当点E与点C重合时,AE=AC>AB
当点E在劣弧︵CB上 (不与点B重合) 时,设AE交CD与H,
AE>AH>AB …… 11分
综上,AE>AB. …… 12分
证明2:当点E在劣弧︵MC上(不与点C重合)时,
连结EC、DF ,∵ AD是⊙O2的直径,即∠AFD=90°
∠EAC=∠EBC=∠DBF=∠DAF
∵ AC=AD 直角△AFD≌直角△AEC
∴ AE=AF …… 9分
证明3:当点E在劣弧︵MC上(不与点C重合)时,
连结EC、DF ,∵ AD是⊙O2的直径,即∠AFD=90°
∵ ∠DBF=∠DAF ∴∠ADF+∠DBF=90°
又∵ ∠DBF=∠EBC ∠ABE+∠EBC=90°
∴ ∠ADF=∠ABE
∵ ∠ABE=∠ACE ∴∠ADF=∠ACE
∵ AC=AD ∴ 直角△AFD≌直角△AEC
∴ AE=AF …… 9分
24(2005广东茂名课改实验区)(本小题10分)
如图,已知直线L与◎○相切于点A,直径AB=6,点P在L上移动,连接OP交◎○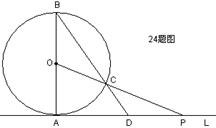 于点C,连接BC并延长BC交直线L于点D,
于点C,连接BC并延长BC交直线L于点D,
(1) 若AP=4, 求线段PC的长(4分)
(2) 若ΔPAO与ΔBAD相似,求∠APO
的度数和四边形OADC的面积(答
案要求保留根号)(6分)
解:24、解:(1)![]() ◎○相切于点A,
◎○相切于点A,
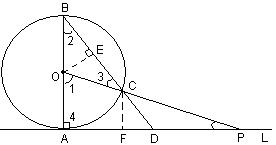
![]() ……………1分
……………1分
![]() ………2分
………2分
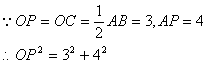
![]() ………………3分
………………3分
![]() ………4分
………4分
(2)![]()
![]() PAO∽ΔBAD,且∠1>∠2,∠4=∠4=900
PAO∽ΔBAD,且∠1>∠2,∠4=∠4=900
![]() ………………………………………………5分
………………………………………………5分
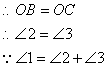
![]() ……………………………6分
……………………………6分
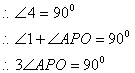
![]() ………………………………7分
………………………………7分
在RtΔBAD中,![]()
![]() …………………8分
…………………8分
方法一:过点O作OE⊥BC于点E,
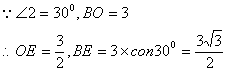
![]() ………………………………9分
………………………………9分
![]()
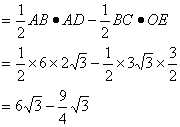
=![]() ……………………………10分
……………………………10分
方法二:在RtΔOAP中,AP=6tan600=3![]() ,OP=2OA=6,
,OP=2OA=6,
![]() DP=AP-AD=3
DP=AP-AD=3![]()
过点C作CF⊥AP于F,![]() ∠CPF=300,
∠CPF=300, ![]() CF=
CF=![]() ………9分
………9分
![]() S四边形OADC=SΔOAP-SΔCDP
S四边形OADC=SΔOAP-SΔCDP
=![]() AP·OA-
AP·OA-![]() DP·CF
DP·CF
=![]() (
(![]()
=![]() …………………10分
…………………10分
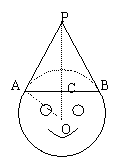
 (2005江苏省课改实验区)如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,求∠A PB的度数.
(2005江苏省课改实验区)如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,求∠A PB的度数.
19.方法一:∵PA、PB切⊙O于A、B,
∴PA=PB ………………………………………………2分
 ∴OA ⊥PA ……………………………………………4分
∴OA ⊥PA ……………………………………………4分
∵∠OAB=25°,∴∠PAB=65° ………………………6分
∴∠APB=180-65°×2=50°…………………………8分
方法二:连结OB,
∵PA、PB切⊙O于A、B,∴OA ⊥PA,OP⊥AB,………2分
∴∠OAP+∠OBP=180°,∴∠APB+∠AOB=180°, ……4分
∵OA=OB,∴∠OAB=∠OBA=25°…………………………6分
 ∴∠AOB=130°,∴∠APB=50°。…………………………8分
∴∠AOB=130°,∴∠APB=50°。…………………………8分
方法三:连结OP交AB于C,
∵PA、PB切⊙O于A、B,∴OA ⊥PA,OP⊥AB,……2分
OP平分∠APB, ……………………………………………4分
∴∠APC=∠OAB=25° ……………………………………6分
∴∠APB=50°。 ……………………………………………8分
 23.(2005江苏泰洲市课改实验区)如图,AB切⊙O于点B,OA交⊙O于C点,过C作DC⊥OA交AB于D,且BD:AD=1:2
23.(2005江苏泰洲市课改实验区)如图,AB切⊙O于点B,OA交⊙O于C点,过C作DC⊥OA交AB于D,且BD:AD=1:2
(1)求∠A的正切值.(3分)
![]() (2)若OC =1,求AB及BC的长.(6分)
(2)若OC =1,求AB及BC的长.(6分)
23.解:(1)(方法一)∵DC⊥OA,OC为半径.∴DC为⊙O的切线………1分
∵AB为⊙O的切线 ∴DC=DB…………………2分
在Rt△ACD中∵ sinA=![]() ,BD:AD=1:2 ∴sinA=
,BD:AD=1:2 ∴sinA=![]() ∴∠A=30°
∴∠A=30°
∴tanA=![]() ………………………………………………3分
………………………………………………3分
(方法二) ∵DC⊥OA,OC为半径.∴DC为⊙O的切线………1分
∵AB为⊙O的切线 ∴DC=DB…………………2分
∵BD:AD=1:2 ∴ CD:AD=1:2
∴设CD= k AD=2k ∴AC=![]() k
k
∴tanA=![]() =
=![]() …………………………………………………3分
…………………………………………………3分
(2)连结OB
∵AB是⊙O的切线 ∴OB⊥AB………………………………4分
在Rt△AOB中 ∵ tanA=![]() OB=1 ∴ AB=
OB=1 ∴ AB=![]() ………6分
………6分
∵∠A=30° ∴∠O=60°………………………………………7分
![]() ∴BC的长=
∴BC的长=![]() =
=![]() ………………………………………9分
………………………………………9分
 23(2005四川内江课该实验区)如图⊙O半径为2,弦BD=
23(2005四川内江课该实验区)如图⊙O半径为2,弦BD=![]() ,A为弧BD的中点,E为弦AC的中点,且在BD上。
,A为弧BD的中点,E为弦AC的中点,且在BD上。
求:四边形ABCD的面积。
23.解:连结OA、OB,OA交BD于F。
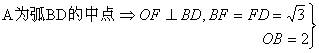
![]()
![]()
![]()
![]()
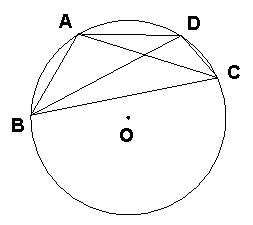
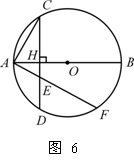 (2005四川课该实验区)如图6,已知AB为⊙O的直径,弦CD⊥AB,垂足为H.
(2005四川课该实验区)如图6,已知AB为⊙O的直径,弦CD⊥AB,垂足为H.
(1) 求证:AH![]() AB=AC2;
AB=AC2;
(2) 若过A的直线与弦CD(不含端点)相交于点E,与⊙O相交于点F,求证:AE![]() AF=AC2;
AF=AC2;
(3) 若过A的直线与直线CD相交于点P,与⊙O相交于点Q,判断AP![]() AQ=AC2是否成立(不必证明).
AQ=AC2是否成立(不必证明).
20.(1) 连结CB,∵AB是⊙O的直径,∴∠ACB=90°. ························· 1分
而∠CAH=∠BAC,∴△CAH∽△BAC . ················································· 2分
∴![]() , 即AH
, 即AH![]() AB=AC2 . ·························································· 3分
AB=AC2 . ·························································· 3分
(2) 连结FB,易证△AHE∽△AFB, ······················································ 4分
∴ AE![]() AF=AH
AF=AH![]() AB, ············································································· 5分
AB, ············································································· 5分
∴ AE![]() AF=AC2 . ···················································································· 6分
AF=AC2 . ···················································································· 6分
(也可连结CF,证△AEC∽△ACF)
(3) 结论AP![]() AQ=AC2成立 . ··································································· 7分
AQ=AC2成立 . ··································································· 7分