初三培优题(一)
1、(山东枣庄市)已知关于x的二次函数![]() 与
与![]() ,这两个二次函数的图象中的一条与x轴交于A, B两个不同的点.
,这两个二次函数的图象中的一条与x轴交于A, B两个不同的点.
(l)试判断哪个二次函数的图象经过A, B两点;
(2)若A点坐标为(-1, 0),试求B点坐标;
(3)在(2)的条件下,对于经过A, B两点的二次函数,当x取何值时,y的值随x值的增大而减小?
2、(重庆)已知:![]() 是方程
是方程![]() 的两个实数根,且
的两个实数根,且![]() ,抛物线
,抛物线![]() 的图像经过点A(
的图像经过点A(![]() )、B(
)、B(![]() ).
).
(1) 求这个抛物线的解析式;
(2)
设(1)中抛物线与![]() 轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(注:抛物线
轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(注:抛物线![]()
![]() 的顶点坐标为(
的顶点坐标为(![]() )
)
(3) 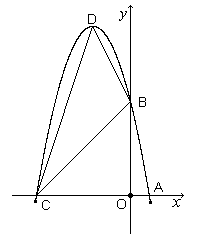 P是线段OC上的一点,过点P作PH⊥
P是线段OC上的一点,过点P作PH⊥![]() 轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
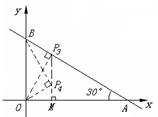
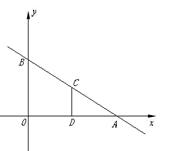 3、(金华)如图,平面直角坐标系中,直线AB与
3、(金华)如图,平面直角坐标系中,直线AB与![]() 轴,
轴,![]() 轴分别交于A(3,0),B(0,
轴分别交于A(3,0),B(0,![]() )两点, ,点C为线段AB上的一动点,过点C作CD⊥
)两点, ,点C为线段AB上的一动点,过点C作CD⊥![]() 轴于点D.
轴于点D.
(1)求直线AB的解析式;
(2)若S梯形OBCD=![]() ,求点C的坐标;
,求点C的坐标;
(3)在第一象限内是否存在点P,使得以P,O,B为顶点的
三角形与△OBA相似.若存在,请求出所有符合条件
的点P的坐标;若不存在,请说明理由.
4、(济南)某校数学研究性学习小组准备设计一种高为60cm的简易废纸箱.如图1,废纸箱的一面利用墙,放置在地面上,利用地面作底,其它的面用一张边长为60cm的正方形硬纸板围成.经研究发现:由于废纸箱的高是确定的,所以废纸箱的横截面图形面积越大,则它的容积越大.
 (1)该小组通过多次尝试,最终选定下表中的简便且易操作的三种横截面图形,如图2,是根据这三种横截面图形的面积
(1)该小组通过多次尝试,最终选定下表中的简便且易操作的三种横截面图形,如图2,是根据这三种横截面图形的面积![]() 与
与![]() (见表中横截面图形所示)的函数关系式而绘制出的图象.请你根据有信息,在表中空白处填上适当的数、式,并完成
(见表中横截面图形所示)的函数关系式而绘制出的图象.请你根据有信息,在表中空白处填上适当的数、式,并完成![]() 取最大值时的设计示意图;
取最大值时的设计示意图;
| 横截面图形 |
|
| |
|
|
|
| |
|
| 30 | 20 | |
|
|
|
| |
|
|
|
|
 (2)在研究性学习小组展示研究成果时,小华同学指出:图2中“底角为
(2)在研究性学习小组展示研究成果时,小华同学指出:图2中“底角为![]() 的等腰梯形”的图象与其他两个图象比较,还缺少一部分,应该补画.你认为他的说法正确吗?请简要说明理由.
的等腰梯形”的图象与其他两个图象比较,还缺少一部分,应该补画.你认为他的说法正确吗?请简要说明理由.
答 案
第一题:(本题满分12分)
解:(l)对于关于x的二次函数y =![]()
由于△=(-m )
2-4×l×![]() =-m2-2<0,
=-m2-2<0,
所以此函数的图象与x轴没有交点……………………………………………… 1分
对于关于x的二次函数 y =![]() .
.
由于△=(-m ) 2-4 ×l×![]() =-m2-2<0,
=-m2-2<0,
所以此函数的图象与x轴没有交点
对于关于x的二次函数![]()
由于![]()
所以此函数的图象与x轴有两个不同的交点.
故图象经过A、B两点的二次函数为![]() …………………3分
…………………3分
(2 )将A(-1,0)代入![]() ,得
,得![]() =0.
=0.
整理,得m2-2m = 0 .
解之,得m=0,或m = 2.…………………………………………………………5分
当m =0时,y=x2-1.令y = 0,得x2-1 = 0.
解这个方程,得x1=-1,x2=1
此时,B点的坐标是B (l, 0).……………………………………………………6分
当m=2时,y=x2-2x-3.令y=0,得x2-2x-3=0.
解这个方程,得x1=-1,x2=3
此时,B点的坐标是B(3,0). …………………………………………………8分
(3) 当m =0时,二次函数为y=x2-1,此函数的图象开口向上,对称轴为x=0,所以当x<0时,函数值 y 随:的增大而减小.……………………………………10分
当m=2时,二次函数为y = x2-2 x-3 = (x-1)2-4, 此函数的图象开口向上,对称轴为x = l,所以当x < l 时,函数值y随x的增大而减小.……………12分
第二题:(1)解方程![]() 得
得![]()
由![]() ,有
,有![]()
所以点A、B的坐标分别为A(1,0),B(0,5).
将A(1,0),B(0,5)的坐标分别代入![]() .
.
得![]() 解这个方程组,得
解这个方程组,得![]()
所以,抛物线的解析式为![]()
(2)由![]() ,令
,令![]() ,得
,得![]()
解这个方程,得![]()
所以C点的坐标为(-5,0).由顶点坐标公式计算,得点D(-2,9).
过D作![]() 轴的垂线交
轴的垂线交![]() 轴于M.
轴于M.
则![]()
![]() ,
,![]()
所以,![]() .
.
(3)设P点的坐标为(![]() )
)
因为线段BC过B、C两点,所以BC所在的值线方程为![]() .
.
那么,PH与直线BC的交点坐标为![]() ,
,
PH与抛物线![]() 的交点坐标为
的交点坐标为![]() .
.
由题意,得①![]() ,即
,即![]()
解这个方程,得![]() 或
或![]() (舍去)
(舍去)
②![]() ,即
,即![]()
解这个方程,得![]() 或
或![]() (舍去)
(舍去)
P点的坐标为![]() 或
或![]() .
.
第三题:(1)直线AB解析式为:y=![]() x+
x+![]() .
……………(3分)
.
……………(3分)
(2)方法一:设点C坐标为(x,![]() x+
x+![]() ),那么OD=x,CD=
),那么OD=x,CD=![]() x+
x+![]() .
.
∴![]() =
=![]() =
=![]() .
………(2分)
.
………(2分)
由题意:![]() =
=![]() ,解得
,解得![]() (舍去) ………(2分)
(舍去) ………(2分)
∴ C(2,![]() ) ………(1分)
) ………(1分)
方法二:∵ ![]() ,
,![]() =
=![]() ,∴
,∴![]() .…(2分)
.…(2分)
由OA=![]() OB,得∠BAO=30°,AD=
OB,得∠BAO=30°,AD=![]() CD.
CD.
∴ ![]() =
=![]() CD×AD=
CD×AD=![]() =
=![]() .可得CD=
.可得CD=![]() . ………(2分)
. ………(2分)
 ∴ AD=1,OD=2.∴C(2,
∴ AD=1,OD=2.∴C(2,![]() ). ………(1分)
). ………(1分)
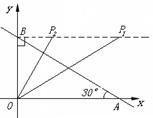
(3)当∠OBP=Rt∠时,如图
①若△BOP∽△OBA,则∠BOP=∠BAO=30°,BP=![]() OB=3,
OB=3,
∴![]() (3,
(3,![]() ).
……(2分)
).
……(2分)
②若△BPO∽△OBA,则∠BPO=∠BAO=30°,OP=![]() OB=1.
OB=1.
∴![]() (1,
(1,![]() ). …………(1分)
). …………(1分)
当∠OPB=Rt∠时
③ 过点P作OP⊥BC于点P(如图),此时△PBO∽△OBA,∠BOP=∠BAO=30°
过点P作PM⊥OA于点M.
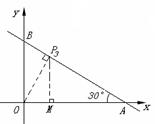 方法一: 在Rt△PBO中,BP=
方法一: 在Rt△PBO中,BP=![]() OB=
OB=![]() ,OP=
,OP=![]() BP=
BP=![]() .
.
∵ 在Rt△PMO中,∠OPM=30°,
∴ OM=![]() OP=
OP=![]() ;PM=
;PM=![]() OM=
OM=![]() .∴
.∴![]() (
(![]() ,
,![]() ). (1分)
). (1分)
 方法二:设P(x ,
方法二:设P(x ,![]() x+
x+![]() ),得OM=x
,PM=
),得OM=x
,PM=![]() x+
x+![]()
由∠BOP=∠BAO,得∠POM=∠ABO.
∵tan∠POM==![]() =
=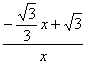 ,tan∠ABOC=
,tan∠ABOC=![]() =
=![]() .
.
∴![]() x+
x+![]() =
=![]() x,解得x=
x,解得x=![]() .此时,
.此时,![]() (
(![]() ,
,![]() ). …(1分)
). …(1分)
④若△POB∽△OBA(如图),则∠OBP=∠BAO=30°,∠POM=30°.
∴ PM=![]() OM=
OM=![]() .
.
∴ ![]() (
(![]() ,
,![]() )(由对称性也可得到点
)(由对称性也可得到点![]() 的坐标).…………(2分)
的坐标).…………(2分)
当∠OPB=Rt∠时,点P在x轴上,不符合要求.
综合得,符合条件的点有四个,分别是:
![]() (3,
(3,![]() ),
),![]() (1,
(1,![]() ),
),![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() ).
).
注:四个点中,求得一个P点坐标给2分,两个给3分,三个给4分,四个给6分.
第四题:(1)表中空白处填写项目依次为![]() ;15;450.························ 3分
;15;450.························ 3分
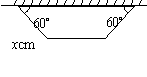
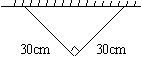
表中![]() 取最大值时的设计示意图分别为:
取最大值时的设计示意图分别为:
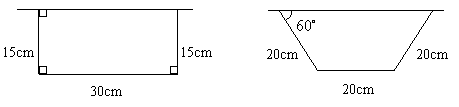 |
(5分)
(2)小华的说法不正确.······················································································ 6分
因为腰长![]() 大于30cm时,符合题意的等腰梯形不存在,所以
大于30cm时,符合题意的等腰梯形不存在,所以![]() 的取值范围不能超过30cm,因此研究性学习小组画出的图象是正确的.·································································································· 7分
的取值范围不能超过30cm,因此研究性学习小组画出的图象是正确的.·································································································· 7分
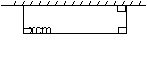
 450
450