2005年初三数学总复习训练题8（圆与直线）
班级_________姓名__________ 得分__________
一、选择题
1、（97南京）直线l与半径为r的⊙O相交，且点O到直线l的距离为5，则r的取值范围是（ ）
A、r>5 B、r=5 C、r<5 D、r≤5
2、（97武汉）已知圆的半径为6.5cm，圆心到直线l的距离为4.5cm，那么这条直线和这个圆的公共点的个数是（ ）
A、0 B、1 C、2 D、不能确定
3、（98广西）等腰△ABC的腰AB＝AC＝4cm，若以A为圆心，2cm为半径的圆与BC相切，∠BAC的度数为（ ）
A、300 B、600 C、900 D、1200
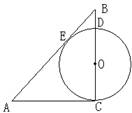
4、（98广州）已知AB是⊙O的直径，CB与⊙O相切于点B，AC＝2AB，则（ ）
A、∠ACB＝600 B、∠ACB＝300 C、ACB＝450 D、BAC＝300
5、（99武汉）已知圆的半径为6.5cm，如果一条直线和圆心距离为6.5cm，那么这条直线和这个圆和位置是（ ）
A、相交 B、相切 C、相离 D、相交或相离
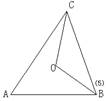
6、（2000武汉）如下左图，在Rt△ABC中，∠C＝900，AC＝4，BC＝3，以BC上一点O为圆心作⊙O与AB相切于E，与AC相切于C，又⊙O与BC的另一交点为D，则线段BD的长为（ ）
A、1 B、 
C、 
D、 
二、填空题
7、（99西安）如图5，在△ABC中，∠ABC＝600，∠ACB＝800，点O是内心，则∠BOC的度数为 __________.
8、（99广西）已知圆的直径为13cm，如果直线和圆心的距离为4.5cm，那么直线和圆的有＿＿个公共点。
9、（98漳州）Rt△ABC的斜边AB＝4，直角边AC＝2，若AB与⊙C相切，则⊙C的半径是 ___ ______。
10、（98甘肃）PA切⊙O于A，PA＝
cm，∠APO＝300，则PO的长为________。
三、解答题：
11、已知四边形ABCD外切于⊙O，四边形ABCD的面积为24，周长24，求⊙O的半径；
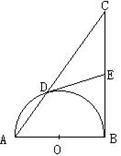
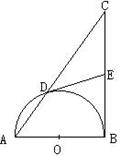
12、如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连结DE.
(1) DE与半圆O相切吗？若相切，请给出证明；若不相切，请说明理由；
(2) 若AD、AB的长是方程x2－10x+24=0的两个根，求直角边BC的长。
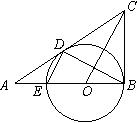
13. 已知：如图，在△ABC中，∠ABC＝90°，O是AB上一点，以O为圆心，OB为半径的圆与AB交于点E，与AC切于点D，连结DB、DE、OC。
⑴从图中找出一对相似三角形（不添加任何字母和辅助线），并证明你的结论；
⑵若AD＝2，AE＝1，求CD的长。
参考答案与提示：
一、选择题
A C D B B C
二、 填空题
7、1100
8、2
9、
10、2
三、 解答题：
11、24=1/2r(AB+BC+CD+DA), AB+BC+CD+DA=24, ∴r=2.
12、 解：（1）DE与半圆O相切. （1分）
证明： 连结OD、BD
∵AB是半圆O的直径
∴∠BDA=∠BDC=90°
∵在Rt△BDC中,E是BC边上的中点
∴DE=BE
∴∠EBD＝∠BDE
∵OB=OD
∴∠OBD=∠ODB (4分)
又∵∠ABC＝∠OBD+∠EBD＝90°
∴∠ODB+∠EBD=90°
∴DE与半圆O相切. (6分)
（2）解：∵在Rt△ABC中，BD⊥AC
∴ Rt△ABD∽Rt△ABC
∴ = 即AB2=AD·AC
∴ AC= (8分)
∵ AD、AB的长是方程x2－10x+24=0的两个根
∴ 解方程x2－10x+24=0得： x1=4 x2=6
∵ AD<AB ∴ AD=4 AB=6
∴ AC=9 （10分）
在Rt△ABC中，AB=6 AC=9
∴ BC===3 （12分）
13、 ⑴略 ⑵ CD＝3