解直角三角形的应用

解直角三角形的应用

一.判断题：

1.在直角三角形中，∠C=90°，siA=，则斜边AB的长为3。 （ ）

2.在Rt△ABC中，∠C=90°，如果sinA=sinB，则∠A=∠B=45°。 （ ）

3.在△ABC中，∠A:∠B:∠C=1:2:3，则BC:AC:AB=1:2:3。 （ ）

4.在Rt△ABC中，∠C=90°，sinA=，则AC大于BC。 （ ）

5.在Rt△ABC中，如果已知一边和一锐角，则△ABC可解。 （ ）

二．选择题：

6.在Rt△ABC中，∠C=90°，∠A≠∠B，则下列等式中正确的是(　 )

（A）sinA-sinB=0 （B）cotA-tanb=0 （C）cosA-cosB=0 （D）sinA+sinB=0

7.已知∠A+∠B=90°,且cosA=，则cosB的值为(　 )

（A）.（B）.（C）.（D）.

8.化简的结果为(　 )

（A）tan50⁰-sin50⁰（B）sin50⁰-tan50⁰. （C）2-sin50⁰-tan50⁰.（D）-sin50⁰-tan50⁰.

9.已知直角三角形的两直角边的比为3:7，则最小角的正弦值为(　 )

（A）.（B）.（C）.（D）.

10.在Rt△ABC中，∠C=90°，tanA=3，AC等于10，则S_△等于(　 )

（A）3 （B）300 （C） （D）150

11.在Rt△ABC中，∠C=90°，sinA:sinB=4:5，则cotA的值是(　 )

（A）.（B）.（C）.（D）.

12.如果直角三角形斜边长为4，一条直角边的长为2，那么斜边上的高为(　 )

（A）2（B）（C）（D）2

13.在Rt△ABC中，∠C=90°，已知α和A，则下列关系式中正确的是(　 )

（A）c=a·sinA（B）c=（C）c=a·cosA（D）c=

14.在Rt△ABC中，∠C=90°,如果cotB=,则下列式子中正确的是(　 )

(A)　  0⁰<B<30⁰.　(B) 60⁰<B<90⁰. (C)30⁰<B<45⁰. (D)45⁰<B<60⁰.

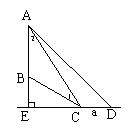
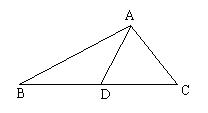15．已知：如右图，在△ABC中，AD是BC边上的中线，∠B=30°，∠C=45⁰,AC=4，求AB和tan∠ADC。

16．在△ABC中，∠C=90°，AD是∠A的平分线，且∠DAC=，BD=，求S_△ABC.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

17.如图,在高出海平面100米的灯塔AB的顶部A,测得正东方和正西方的两艘船C、D的俯角分别为30⁰和

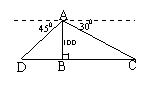45⁰,求这两艘船之间的距离CD.

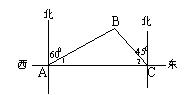
18.如图,一只船从港口C出发向西航行.­出发时,在船上观察小岛B在北偏西45⁰的方向,小岛B距离港口C10­海里.航行到达A处时,再观察小岛B,在北偏东60⁰的方向.­求这只船从C到A航行了多少海里?

­

19.如图,在山顶上有一电视塔,在塔顶B处测得地面上一点A的俯角α=60⁰,在塔底C处测得A的俯角

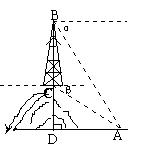β=45⁰,已知塔高BC=60米,求山高CD。

20.如图,,要测底部不能到达的烟囱AB的高度,从烟囱底部在同一水平线上的C、D两处,测得

∠CDA=45⁰­∠ECB=30⁰,CD=a米,∠ECA=60⁰,求烟囱AB的高度.

­

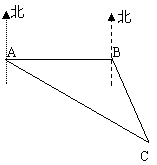21.台湾“华航”客机失事后，祖国大陆海上搜救中心立即通知位于A、B两处的上海救捞人局所属专业救助轮“华意”轮、“沪救12”轮前往出事地点协助搜索。接到通知后，“华意”轮测得出事地点C在A的南偏东60°、“沪救12”轮测得出事地点C在B的南偏东30°。已知B在A的正东方向，且相距100浬，分别求出两艘船到达出事地点C的距离。