★ 机密 ★
2006年一中高中保送生考试
数 学 试 卷
考试时间:120分钟 满分:120分
注意事项：
1．考生答题前将本页密封线内的项目和座位号填写清楚。
2．考生答卷需用蓝（黑）色钢笔或圆珠笔直接答在试题卷上。
| 题 号 | 一 | 二 | 三 | 总 分 | |||||||||
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | ||||
| 分 数 | |||||||||||||
| 得 分 | 评卷人 | 一、填空题：本大题共12个小题，每小题2分，共24分． 请将答案填在题中横线上． |
1.
在函数
中，自变量
的取值范围_______.
2.
分解因式：
.
3.
五张标有１,2,3,4,5的卡片除数字外其它没有任何区别,现在将它们背面朝上,从中任取一张,得到卡片的数字为偶数的概率为_______.
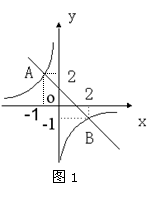
4. 如图1，一次函数与反比例的图像相交于A、B两点，则图中使反比例函数的值小于一次函数的值的x的取值范围是___________.
5.
等腰三角形ABC中，BC=8,AB、AC的长是关于x的方程
的两根,则m的值为___________.
6.
在□
4的空格中,任意填上“+”或“-”,共有______种不同的代数式,其中能够构成完全平方式的概率为__________.
7.
以A(3,4)为圆心的圆与两坐标轴共有三个公共点,⊙A的半径是________.
8.
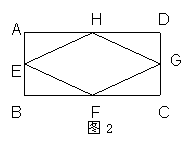
如图2，在矩形 ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点，若
，四边形EFGH的周长为40cm,则矩形ABCD的面积为_______
.
9.
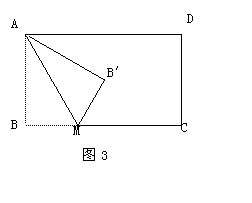
如图3一张长方形纸片ABCD，其长AD为 a,宽AB为b(a>b),在BC边上选取一点M,将
沿AM翻折后B至
的位置,若为长方形纸片ABCD的对称中心,则
的值为_________.
10.
某超市推出如下优惠方案：(1)一次性购物不超过100元不享受优惠(2)一次性购物超过100元但不超过300元一律9折(3)一次性购物超过300元一律8折.小李两次购物分别付款80元,252元,如果他一次性购买与上两次相同的商品,应付款________________元.
11. 在计算机程序中,二叉树是一种表示数据结构的方法,如图4一层二叉树的结点总数为1;二层二叉树的结点的总数为3;三层二叉树的结点总数为7;四层二叉树的结点总数为15……，照此规律，七层二叉树的结点总数为_______.
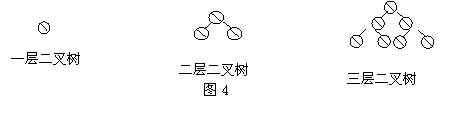
12.
已知矩形ABCD的长AB=4,宽AD=3,按如图5所示放置在直线MP上,然后不滑动地转动矩形,当它转动一周时(A－
)，顶点A所经过的路线长等于______.
| 得 分 | 评卷人 | 二、选择题：本大题共6个小题，每小题3分，共18分．在每小题给出的四个选项中，只有一项是符合题目要求的． |
13.为筹备班级的初中毕业联欢会,班长对全班学生爱吃哪几种水果作了民意调查,那么最终买什么水果,下面的调查数据中最值得关注的是( )
A、众数 B、平均数 C、中位数 D、加权平均数
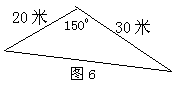
14.某市“旧城改造”中计划在市内一块如图6的三角形空地上种植某种草皮以美化环境，已知种植草皮每平方米售价a元，则购买这种草皮至少需( )
A、450a B、225a C、150a D、300a
15.如图7是由一些相同的小正方体构成的几何体的三视图，则构成这个几何体的小正方体的个数是( )
A、5 B、6 C、7 D、8
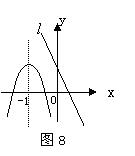16.已知抛物线和直线
在同一直角坐标系中的图像如图8所示，抛物线的对称轴为直线x=-1,
是抛物线上的点，
是直线上的点,且
,则
的大小关系为( )
A、
B、
C、
D、
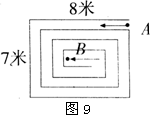
17.如图9“回”字形的道路宽为1米，整个“回”字形的长为8米，宽为7米，一个人从入口点A沿道路中央走到终点B,他共走了( )
A、55米 B、55.5米
C、56米 D、56.5米
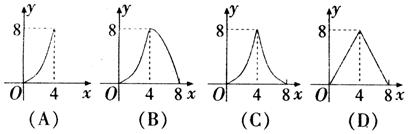
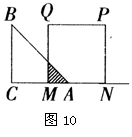
18.如图10,等腰直角三角形ABC(
)的直角边长与正方形MNPQ的边长均为4cm,CA与MN在同一直线上,开始时A点与M点重合,让
ABC向右平移,直到C点与N点重合时为止,设
与正方形MNPQ的重叠部分(图中阴影部分)的面积为
,MA的长度为
,则y与x之间的函数关系大致为( )
三、 本大题共10题,共78分,解答应写出文字说明、演算步骤或推理过程．
| 得分 | 评卷人 |
19.（本题5分）
计算:
| 得分 | 评卷人 |
20.(本题6分)
解方程组:
| 得分 | 评卷人 |
21.(本题6分)
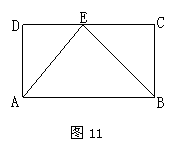
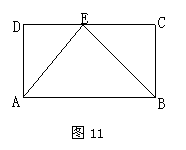如图11，四边形ABCD为矩形,动点E在DC边上移动,但点E不与点D、C重合.
(1)当点E移动到什么位置时,
≌
?请说明你的结论.
(2)当
为多少度时, ∽
?请说明你的结论.
| 得分 | 评卷人 |
22.(本题8分)
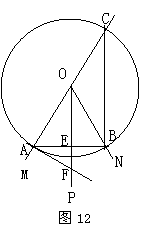
如图12，小明按下面的方法作
的平分线：
① 反向延长射线OM；
②
以O为圆心，任意长为半径作圆，分别交的两边与点A、B,交射线OM的反向延长线于点C;
③ 连接OB；
④
以O为顶点,OA为一边作
.
(1)根据上述作图,射线OP是的平分线吗?并说明理由.
(2)若过点A作⊙O的切线交射线OP于点F,连接AB交OP于点E,当
,OF=10时,求AE的长
| 得分 | 评卷人 |
23.(本题6分)
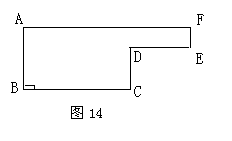
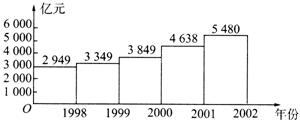如图13给出了我国从1998年～2002年每年教育经费投入的情况.
(1) 由图可见, 1998年～2002年这五年内,我国教育经费投入呈现出___________趋势;
(2)
|
(3) 如果我国的教育经费从2002年的5480亿元增加到2004年的7891亿元,那么这两年的教育经费平均增长率为多少?(结果精确到0.01)
| 得分 | 评卷人 |
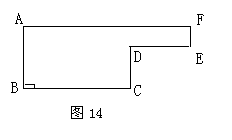
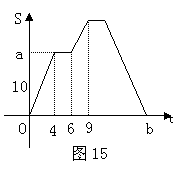24.(本题8分)已知动点P以每秒2cm的速度沿图14的边框按从B→C→D→E→F→A的路径移动，相应的
的面积S关于时间t的函数图像如图15所示,若AB=6cm,试回答下列问题:
(1)、图14中的BC的长是多少?
(2)、图15中的a多少?
(3)、图14中的图形面积是多少?
(4)、图15中的b是多少?
| 得分 | 评卷人 |
25.(本题7分)
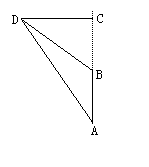
如图16,一人工湖的对岸有一条笔直的小路,湖上原有一座小桥与小路垂直相通,现小桥有一部分已断裂,另一部分完好.站在完好的桥头A测得路边的小树D在它的北偏西
,前进32米到断口B处,又测得小树D在它的北偏西
,请计算小桥断裂部分的长.(结果保留整数)
| 得分 | 评卷人 |
26.(本题9分)
某果农收获荔枝30吨,香蕉13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往某市，已知甲种货车 可装荔枝4吨和香蕉1吨，乙种货车可装荔枝香蕉各2吨.
(1)该果农安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(2)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1300元,则该果农应选择哪种方案,才能使总运费最少?最少运费是多少元?
| 得分 | 评卷人 |
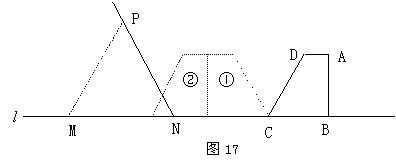
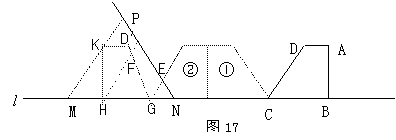
27.(本题10分)已知,如图17,在直角梯形ABCD中,
AD∥BC,BC=5cm,CD=6cm,
.等边三角形MPN(N为不动点)的边长为acm,边MN和直角梯形ABCD的底边BC都在直线上,NC=8cm .将直角梯形ABCD向左翻折
,翻折一次得图形①,翻折二次得图形②,如此翻折下去.
(1) 将直角梯形ABCD向左翻折二次,如果此时等边三角形的边长
,这时两图形重叠部分的面积是多少?
(2) 将直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积等于直角梯形ABCD的面积,这时等边三角形的边长a至少应为多少?
(3) 将直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积等于直角梯形ABCD的面积的一半,这时等边三角形的边长应为多少?
| 得分 | 评卷人 |
28.(本题13分)
在直角坐标系XOY中,O为坐标原点,A,B,C三点的坐标分别为A(5,0),B(0,4),C(-1,0).点M和点N在x轴上(点M在点N的左边),点N在原点的右边,作MP⊥BN,垂足为P(点P在线段BN上,且点P与点B不重合),直线MP与y轴相交于点G,MG=BN.
(1)求经过A,B,C三点的抛物线的表达式;
(2)求点M的坐标;
(3)设ON=t,
的面积为S,求S与t的函数关系式,并写出自变量t的取值范围;
(4)过点B作直线BK平行于x轴,在直线BK上是否存在点R,使
为等腰三角形,若存在,请直接写出点R的坐标,若不存在,请说明理由.
| |
2006年一中高中保送生考试
数学试卷参考答案及评分标准
一、填空题：本大题共12个小题，每小题2分，共24分．
1．
且
2. 
3.
4．x＜-1或0＜x＜2 5.25或16 6.8；0.5
7．4或5
8.192
9. 
10.316或288
11.127
12.
二、选择题：本大题共6个小题，每小题3分，共18分
13．A 14.C 15.D 16.D 17.C 18.B
三、本大题共10题,共78分.
19.（本题5分）
解：原式=
（3分）
=
（4分）
=
（5分）
20.(本题6分)
解：由①+②得
③
②-①得 
④
（4分）
由③④组成方程组为
③+④得x=-1
③-④得y=2 ∴原方程组的解为
(6分)
21.(本题6分)
（1）当点E为DC的中点时,≌.(1分)
∵点E为DC的中点
∴DE=EC
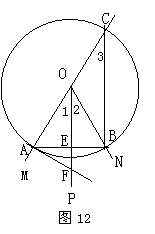
在矩形ABCD中，AD=BC，∠C=∠D=90°
∴在和中
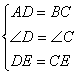∴ ≌（3分）
（2）当为90度时, ∽（4分）
∵=90°
∴
又
∴
且∠C=∠D=90°
∴∽ （6分）
22.(本题8分)
（1） 射线OP是的平分线.（1分）
∵和∠3所对的弧是同弧
∴=2∠3 （2分）
又∵∠1=∠3
∠1+∠2=2∠3
∴∠1=∠2=∠3
∴OP是的平分线 （4分）
（2） ∵AF切于⊙O
∴OA⊥AF
∵=60°
∴∠1=30° （5分）
在Rt△OAF中
且OF=10
∴
（6分）
∵OA=OB
且 =60°
∴△OAB是等边三角形
∴
（8分）
23.(本题6分)
（1） 逐年增长 （1分）
（2） 
（2分）
（3） 设这两年的教育经费的平均增长率为x，则
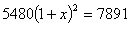（4分）
解得
（舍去）
∴x=0.20=20%
∴这两年的教育经费平均增长率为20% (6分)
24.(本题8分)
（1） 由图知，点P由B运动到C时用了4 秒，
所以
（2分）
（2）
（4分）
（3） 在 C→D的运动中，
的面积不变，
所以用了2秒
所以
在 D→E的运动中，用了3秒
所以
所以
（6分）
（4） 因为AF=14，所以由F→A需7秒
所以b=9+1+7=17秒 （8分）
25.(本题7分)
依题意 作图（画出图形1分）
延长AB交小路于C点，设BC=x
因为
，AC⊥DC
所以BC=CD=x (2分)
在Rt△ADC中 
所以 
，
即
（5分）
所以
米，即断裂部分的长约为44米.（7分）
26.(本题9分)
解：设安排甲种货车x辆，则乙种货车（10-x）辆 （1分）
依题意，得
（3分）
解这个不等式组得 5≤x≤7
因为x是整数，所以x可取5，6，7 （4分）
即安排甲、乙两种货车有3种方案：
①甲种货车5辆，乙种货车5辆
②甲种货车6辆，乙种货车4辆
③甲种货车7辆，乙种货车3辆 （6分）
27.(本题10分)
解：(1)因为CB=5 ，CN=8 所以GN=2
又因为∠PNM=60°且∠EGN=60°
所以△EGN为正三角形
所以 △EGN的高为
所以
（3分）
（2）在直角梯形ABCD中，因为CD=6，∠DCB=60°，
所以AB=
在Rt△KHM中，
，
所以MN=2+5+3=10 （6分）
（3） S梯形ABCD=
当MP经过H点时，交D′G于F，
则
＞
S梯形ABCD
所以HG＜5，设HG=x，则有
所以S公共部分=
所以
因为 GN=2
所以等边三角形PNM的边长a为（
）cm（10分）
28.(本题13分)
解： (1)设所求抛物线的表达式为：
由题意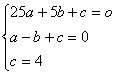，得
解得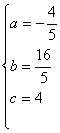
所以所求的表达式为
（3分）
（2）依题意，分两种情况：
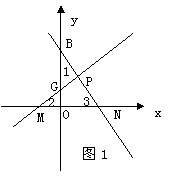
① 当点M在原点的左边（如图1）时，
在Rt△BON中， ∠1+∠3=90°
因为MP⊥PN，所以 ∠2+∠3=90°，
所以 ∠1=∠2
在Rt△BON和Rt△MOG中，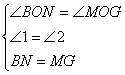
所以 Rt△BON≌Rt△MOG
所以OM=OB=4. 所以M点的坐标为（-4，0）（5分）
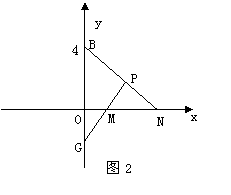
② 当点M在原点的右边（如图2）时，同理可证OM=OB=4.
此时M点的坐标为（4，0）. （7分）
(3) 图1中，Rt△BON≌Rt△MOG，所以OG=ON=t.
所以
=2t(其中0＜t＜4
（9分）
图2中，同理可得S=2t,其中t＞4.
所以所求的函数关系式为S=2t,
t的取值范围为t＞0且t≠4. （11分）
(4) 存在点R，使△ORA为等腰三角形，其坐标为：
.
（13分）
2006年一中高中保送生考试
数学试卷命题思路
为了达到择优录取一中保送生的目的, 我们数学命题组把试卷的难易比例确定为2:6:2。本试卷题型参照中考试卷题型，旨在考查学生的创新能力和综合运用知识的能力，试卷涉及的知识面较广，充分考查学生的实践能力,以及综合运用数学知识分析问题和解决问题的能力。以下分别从各题具体谈谈本次命题的意图：
一、填空题是在考查学生基础知识的同时，更突出考查了学生的解题能力，识图能力。从函数图象求自变量取值范围（第4题），到几何图形的对折、翻转(第12题)，都体现了数形结合的思想。适当地加入多解题,能很好地考查学生应用基础知识的能力和在解题中的思维的缜密性。
二、 选择题的计算量较少，主要考查学生在阅读题目的基础上，对给出的图形是否能较快地进行分析、理解、得出结论.
三、 解答题
（1） 第19、20题为计算题，其中第19题是基础题，考查学生对指数、二次根式等的计算能力；第20题为解方程组，在学生熟练掌握常规方法的基础上，能结合方程组的特征，适当变形，运用“整体思想”进行求解。
（2） 第21、22题为证明题，考查学生基础知识的运用及证明过程的严谨性，具有一定的开放性，需要学生有较扎实的基础知识和较强的逻辑思维能力。
（3） 第23题是统计知识的综合应用题，是一道贴近当前形势、合乎情理的情景题，从中考查了平均数、增长率的有关知识及基本的识图能力。
（4） 第24题是通过文字和图象共同提供信息，题目新颖、灵活。图象中的折线说明了不同的自变量对应着不同的规律。
（5） 第25、26题是情景应用题，此类题型以现实生活为背景，给人耳目一新的感觉，这类题目涉及的数学知识不深，但立意新颖，有利于考查学生应用数学的“建模思想”解决问题的能力。
（6） 第27题是根据新课标的要求，充分运用对称、平移等知识解决几何图形中的变换问题，此类问题要抓住图形的变化过程，认真比较变化前后的图形，从中寻找解题思路。
（7） 第28题主要考查目的是函数及其应用，特别要注意分类讨论的数学思想。这类问题首先要认真审题，分析题意，抓住分类的对象，要求学生具有较强的分析问题及解决问题的综合能力。
数学命题组
2006.5.14