归纳与猜想型问题
1、猜想数式规律
例1（云南）观察按下列顺序排列的等式：
；
；
；
；
； ……
猜想：第
个等式（为正整数）用表示，可以表示成________________.
2、猜想图形规律
 |
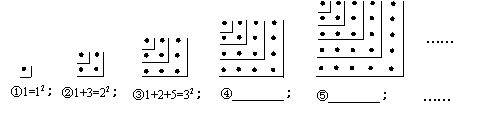例2（河北课改实验区）观察图2所示的点阵图和相应的等式，探究其中的规律：
（1）在④和⑤后面的横线上分别写出相应的等式；
（2）通过猜想写出与第n个点阵相对应的等式.
3、猜想数值结果
例3．如图，细心观察图形，认真分析各式，然后解答问题：
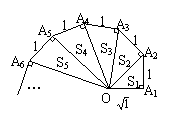（）2＋1＝2 S1＝
（）2＋1＝3 S2＝
（）2＋1＝4 S3＝
⑴请用含有n（n是正整数）的等式表示上述变化规律；⑵推算出OA10的长；
⑶求出S12＋S22＋S32＋…＋S102的值．
4、猜想数量关系
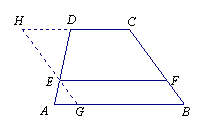
例4（江苏连云港）（1）如图5，在梯形ABCD中，AB∥CD，
，
，E为AD边上的任意一点，EF∥AB，且EF交BC于点F，某学生在研究这一问题时，发现如下事实：
①当
时，有
；
②当
时，有
；
③当
时，有
．
当
时，参照上述研究结论，请你猜想用k表示DE的一般结论，并给出证明；
 |
（2）现有一块直角梯形田地
（如图6所示），其中AB∥CD，
，
310米，
170米，
70米．若要将这块地分割成两块，由两农户来承包，要求这两块地均为直角梯形，且它们的面积相等．请你给出具体分割方案．
5、猜想变化情况
例5（山东青岛）四边形是大家最熟悉的图形之一，我们已经发现了它的许多性质.只要善于观察、乐于探索，我们还会发现更多的结论.
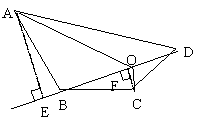
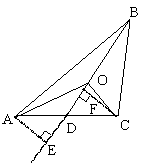(1)四边形一条对角线上任意一点与另外两个顶点的连线，将四边形分成四个三角形(如图7)，其中相对的两对三角形的面积之积相等.你能证明这个结论吗？试试看.
已知：在四边形ABCD中，O是对角线BD上任意一点（如图7）；求证：S△OBC·S△OAD=S△OAB·S△OCD.
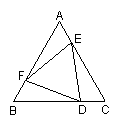
(2)在三角形中（如图8），你能否归纳出类似的结论？若能，写出你猜想的结论，并证明：若不能，说明理由.
课堂练习
1．（2005年常州）如图，已知
为等边三角形，
、
、
分别在边
、
、
上，且
也是等边三角形．
（1）除已知相等的边以外，请你猜想还有哪些相等线段，并证明你的猜想是正确的；
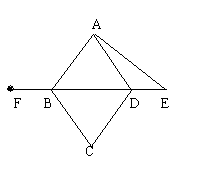（2）你所证明相等的线段，可以通过怎样的变化相互得到？写出变化过程．
2．（2005年北京丰台）已知：如图，四边形ABCD是菱形，E是BD延长线上一点，F是DB延长线上一点，且DE=BF。请你以F为一个端点，和图中已标明字母的某一点连成一条新的线段，猜想并证明它和图中已有的某一条线段相等（只须证明一组线段相等即可）。
（1）连结____________；
（2）猜想：______=______；
（3）证明：
3．随着信息技术的高速发展，电话进入了千家万户，据调查某校初三⑴班的同学家都装上了电话，暑假期间全班每两个同学都通过一次电话，如果该班有56名同学，那么同学们之间共通了多少次电话？
为解决该问题，我们可把该班人数n与通电话次数s间的关系用下列模型来表示：
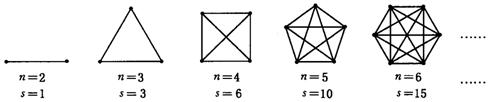
⑴若把n作为点的横坐标，s作为纵坐标，根据上述模型中的数据，在给出的平面直角坐标系中，描出相应各点，并用平滑的曲线连接起来；
⑵根据图中各点的排列规律，猜一猜上述各点会不会在某一函数的图象上？如果在，求出该函数的解析式；
⑶根据⑵中得出的函数关系式，求该班56名同学间共通了多少次电话．
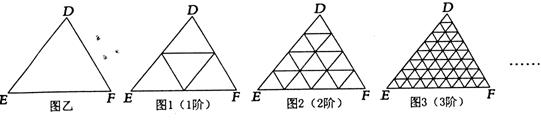
4．定义：若某个图形可分割为若干个都与他相似的图形，则称这个图形是自相似图形。
探究：一般地，“任意三角形都是自相似图形”，只要顺次连结三角形各边中点，则可将原三角形分割为四个都与它自己相似的小三角形。我们把△DEF（图乙）第一次顺次连结各边中点所进行的分割，称为1阶分割（如图1）；把1阶分割得出的4个三角形再分别顺次连结它的各边中点所进行的分割，称为2阶分割（如图2）……依次规则操作下去。n阶分割后得到的每一个小三角形都是全等三角形（n为正整数），设此时小三角形的面积为Sn.
⑴若△DEF的面积为10000，当n为何值时，2＜Sn＜3？（请用计算器进行探索，要求至少写出三次的尝试估算过程）
⑵当n＞1时，请写出一个反映Sn－1，Sn，Sn＋1之间关系的等式（不必证明）。
5．据我国古代《周髀算经》记载，公元前1120年商高对周公说，将一根直尺折成一个直角，两端连结得一个直角三角形，如果勾是三、股是四，那么弦就等于五。后人概括为“勾三、股四、弦五”。⑴观察：3，4，5；5，12，13；7，24，25；……，发现这些勾股数的勾都是奇数，且从3起就没有间断过。计算（9－1）、（9＋1）与（25－1）、（25＋1），并根据你发现的规律，分别写出能表示7，24，25的股和弦的算式；
⑵根据⑴的规律，用n（n为奇数且n≥3）的代数式来表示所有这些勾股数的勾、股、弦，合情猜想他们之间二种相等关系并对其中一种猜想加以证明；
⑶继续观察4，3，5；6，8，10；8，15，17；……，可以发现各组的第一个数都是偶数，且从4起也没有间断过。运用类似上述探索的方法，直接用m（m为偶数且m＞4）的代数式来表示他们的股和弦。
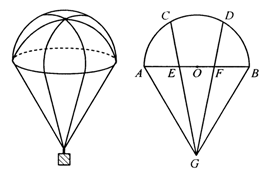6．（2005年河南）空投物资用的某种降落伞的轴截面如图所示，
是等边三角形，
、是以为直径的半圆
的两个三等分点，
、
分别交于点、，试判断点、分别位于所在线段的什么位置？并证明你的结论（证明一种情况即可）
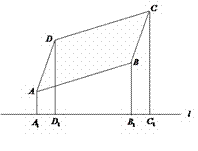7．（2005年潍坊）如图，已知平行四边形
及四边形外一直线
，四个顶点
到直线的距离分别为
．
（1）观察图形，猜想得满足怎样的关系式？证明你的结论．
(2)现将向上平移，你得到的结论还一定成立吗？请分情况写出你的结论．
8.（2005年锦州）如图a，△ABC和△CEF是两个大小不等的等边三角形，且有一个公共顶点C，连接AF和BE.
(1)线段AF和BE有怎样的大小关系?请证明你的结论；
(2)将图a中的△CEF绕点C旋转一定的角度，得到图b，(1)中的结论还成立吗?作出判断并说明理由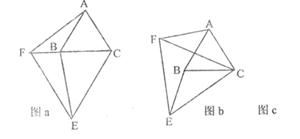
；
(3)若将图a中的△ABC绕点C旋转一定的角度，请你画山一个变换后的图形c(草图即可)，(1)中的结论还成立吗?作出判断不必说明理由；
(4)根据以上证明、说理、画图，归纳你的发现.
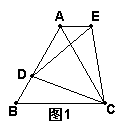
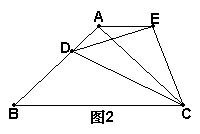
9．（2005年苏州）(1)如图一，等边ΔABC中，D是AB边上的动点，以CD为一边，向上作等边ΔEDC，连结AE。求证：AE∥BC；
(2)如图二，将(1)中等边ΔABC的形状改成以BC为底边的等腰三角形，所作ΔEDC改成相似于ΔABC。请问：是否仍有AE∥BC？证明你的结论。
 |  | ||