操作型问题选
【考点透视】
纵观近年来全国各省市的中考试题,操作型问题已日渐成为中考热点之一 .它体现了新课程标准强调学生主动参与,勤于动手,乐于探究,经历学习过程的新理念.
操作型问题能让学生经历观察,操作,实验,猜想,验证的探究过程.不仅能考查学生的空间观念,对图形的认识,图形的变换,图形的设计,图形的直觉判断能力,而且还能考查学生的分析综合,抽象概括逻辑推理的能力,是学生展示个体思维发散创新的好平台.操作型问题一般包括作图问题,分割组合图形问题,图形的折叠问题和图形移动等问题.
解决这类问题,要理解掌握轴对称轴、中心对称及点的轨迹的基本性质,审清题意,学会运用图形的平移变换、翻折变换和旋转变换. 注意运用分类讨论、类比猜想、验证归纳等数学思想方法,灵活地解决问题.在平时的学习中,要注重操作习题解题训练,提高思维的开放性,培养创新能力.
 【典型例题】
【典型例题】
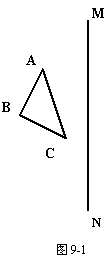
例1如图9-1,在正方形网络上有一个△ABC.
(1)作△ABC关于直线MN的对称图形
(不写作法);
(2)若网络上的最小正方形的边长为1,
求△ABC的面积.
(2003年浙江绍兴市中考试题)
分析:(1)观察图形,先作出点A、B、C关
于直线MN的对称点A1、B1、C1,连结A1B1、、
B1C1、C1A1得△A1B1C1.
(2)S△ABC等于点A、B、C所在边的矩形面积与三个直角三角形面积和的差.
解:(1)作图(略).
(2)此三角形面积为:S△ABC=2×3-2×(![]() ×1×2)-
×1×2)-![]() ×1×3=6-2-
×1×3=6-2-![]() =
=![]()
说明:本题利用轴对称性质来作图. 常见的作图题依据着轴对称、中心对称及点的轨迹的性质来作图.
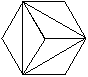
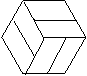
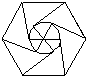
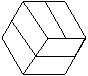
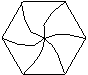
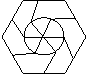
例2某地板厂要制作正六边形形状的地板砖,为了适应市场多样化需求,要求在地板砖上设计的图案能够把正六边形6等分,请你帮助他们设计等分图案(至少设计两种).
(2003年甘肃省中考试题)
分析:由题意得:本例属于等分分割图形问题,正六边形既是轴对称图形又是中心对称图形.设计图案的关键:以正六边形的6个顶点和正六边形的中心为顶点分割设计成6等分图案.
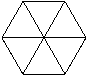
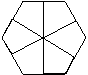
解:(答案不惟一,在下图9-2中任选两种).
 |  |  | |||||
 | |||||||
 | |||||||||
 |  | ||||||||
 | |||||||||
| |||||||||
说明:本例属于等分分割图形问题,与此例类似的如将平行四边形、矩形、正方形分割成4等分等.这类问题解决,只有抓住被分割图形的中心及图形的顶点后,发挥个人的想象力,才能创造性地设计出图案.
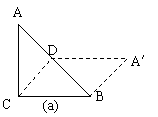
例3如图9-3,把一个等腰直角三角形ABC沿斜边上的高CD(裁剪线)剪一刀,从这个三角形中裁下一部分,与剩下部分能拼成一个平行四边形A′BCD(见示意图a).
(以下探究过程中有画图要求的,工具不限,不必写画法和证明.)
探究一:
(1)想一想——判断四边形A′BCD是平行四边形的依据是 ;

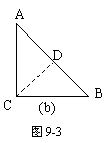 (2)做一做——按上述的裁剪方法,请你拼一个与图(a)位置或形状不同的平行四边形,并在图(b)中画出示意图.
(2)做一做——按上述的裁剪方法,请你拼一个与图(a)位置或形状不同的平行四边形,并在图(b)中画出示意图.
 |
探究二:
在直角三角形ABC中,请你找出其他的裁剪线,把分割成的两部分拼出不同类型的特殊四边形.
(1)试一试——你能拼得不同类型的特殊四边形有 ,它们的裁剪线分别是 ;
(2)画一画——请在图(c)中画出一个你拼得的特殊四边形示意图.
(2003年浙江省丽水市中考试题)
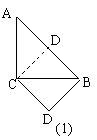 分析:探究二:本例属于分割图形后,再重新组合图形问题.由于裁剪线的不定性,使组合图形变得更加多姿多彩.重新组拼图形的关键是找出不同类型的特殊四边形:平行四边形、矩形、等腰梯形、直角梯形再用实验和类比的方法来寻找答案.
分析:探究二:本例属于分割图形后,再重新组合图形问题.由于裁剪线的不定性,使组合图形变得更加多姿多彩.重新组拼图形的关键是找出不同类型的特殊四边形:平行四边形、矩形、等腰梯形、直角梯形再用实验和类比的方法来寻找答案.
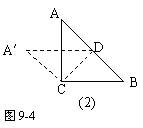 解:探究一:
解:探究一:
|
|
(2)(只要画出图9-4(1),(2)之一的
示意图).
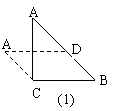
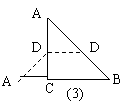
探究二:平行四边形、矩形、等腰梯形、直角梯形. 三角形ABC的中位线(或一条三角形的中位线)(注:若写出直角梯形,并指出这条裁剪线是“把一条直角边分成![]() :1的两段,且平行于另一条直角边(或斜边)的线段”,才算正确.)
:1的两段,且平行于另一条直角边(或斜边)的线段”,才算正确.)
 | |||||
 | |||||
 | |||||
(2)只要画出图9-5中(1)~(6)之一的示意图.
说明:本例探究二中,由于裁剪线的不定性,给重新组合图形留下较大的创新空间.解答此类问题,常用的方法有实验法、分析法、类比法、联想法和验证法.想一想:探究一中,能否拼成菱形?请说明理由.
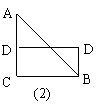
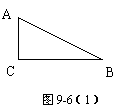
例4阅读下面短文:如图9-6(1)所示,△ABC是直角三角形,∠C=900,现在△ABC补成矩形,使△ABC的两个顶点为矩形一边的两端点,第三个顶点落在矩形这一边上,那么符合要求的矩形可以画出两个:矩形ACBD和矩形AEFB(如图9-6(2)所示).
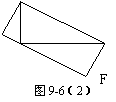
|
|
| |||||
| |||||
| |||||
解答问题:
(1)设图9-6(2)所示矩形ACBD和矩形AEFB的面积分别为S1、S2,则S1 S2(填“>”、“=”、“<”)
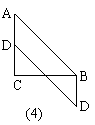
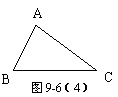
(2)如图9-6(3)所示, △ABC是钝角三角形,按短文中的要求把它补成矩形,那么符合要求的矩形可以画出 个 ,利用图9-6(3)把画出来.
 | |||
 | |||
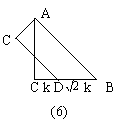
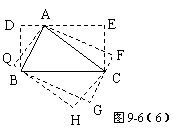
(3)如图9-6(4)所示,△ABC是锐角三角形三边满足BC>AC>AB,按短文中的要求把它补成矩形,那么符合要求的矩形可以画出 个,利用图9-6(4)把它出来.
(4)在(3)中所画出的矩形中,哪一个的周长最小?为什么?
(2002年陕西省中考试题)
分析:(2)只能以AB为一边,作一个矩形;(3)可以锐角△ABC的三边作三个矩形;
(4)由(1)类推(3)中的三个矩形的面积相等,设其面积为S,用S与a、b、c三边分别表示三个矩形的周长L1、L2、L3,用作差法类比三个矩形的周长的大小.
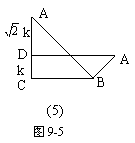
解:(1)S1=S2;(2)一个(如图9-6(5));(3)三个(如图9-6(6));
 | |||
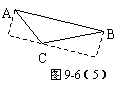 | |||
(4)以AB为边的矩形周长最小. 设矩形BCED、ACHQ、ABGF的周长分别为L1、L2、L3,BC=a,AC=b,AB=c.易知这三个矩形的面积相等.令其面积为S,则有,L1=![]() +2a,L2=
+2a,L2=![]() +2b,L3=
+2b,L3=![]() +2c.∵L1- L2=
+2c.∵L1- L2=![]() +2a-(
+2a-(![]() +2b)=2(a-b)·
+2b)=2(a-b)·![]() . 而ab>S,a>b,∴L1- L2>0,即L1> L2,同理L2> L3. ∴以AB为边的矩形周长最小.
. 而ab>S,a>b,∴L1- L2>0,即L1> L2,同理L2> L3. ∴以AB为边的矩形周长最小.
![]() 说明:本例要求在熟悉按要求补图、组合图形的基础上,分析、归纳、类比一此量的变化.另外通过解答可以发现本例有三个规律:一是所画矩形个数的规律(一个、二个、三个).二是符合要求的矩形的面积的规律(各图中矩形面积均为原三角形面积的2倍等). 三是矩形周长的规律(以短边为矩形一边的矩形周长最短).
说明:本例要求在熟悉按要求补图、组合图形的基础上,分析、归纳、类比一此量的变化.另外通过解答可以发现本例有三个规律:一是所画矩形个数的规律(一个、二个、三个).二是符合要求的矩形的面积的规律(各图中矩形面积均为原三角形面积的2倍等). 三是矩形周长的规律(以短边为矩形一边的矩形周长最短).
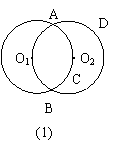
例5已知两个等圆⊙O1和⊙O2相交A、B两点,⊙O1经过O2,点C是AO2B上任一点(不与A、O2、B重合),连结BC并延长交⊙O2于D,连结AC、AD.
(1) 图9-7(1)供操作测量用,(测量时使用刻度尺和圆规)将图9-7(1)按题中叙述补充完整,并观察或度量AC、CD、AD三条线段的长短,通过观察和度量,说出三条线段的长度之间存在怎样关系?
(2)
![]() 猜想结论(求证部分),并证明你的猜想,在补充完整图9-7(1)中进行证明.
猜想结论(求证部分),并证明你的猜想,在补充完整图9-7(1)中进行证明.
(3) 如图9-7(2),若C点是BO2的中点,AC与O1O2相交于点E. 连接O1C、O2C,
求证CE2= O1O2·E O2.
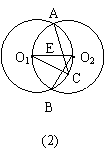
![]()
![]()
图9-7
(2002四川眉山市中考试题)
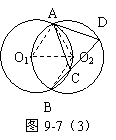 分析:(1)画图测量,易得AC=CD=AD. (2)欲证△ACD为正三角形,可利用圆周角定理及其推论证明△ACD每一个内角都等于600即可.(3)欲证CE2=
O1O2·E O2.只需证:△O1O2C∽△CO2E.
分析:(1)画图测量,易得AC=CD=AD. (2)欲证△ACD为正三角形,可利用圆周角定理及其推论证明△ACD每一个内角都等于600即可.(3)欲证CE2=
O1O2·E O2.只需证:△O1O2C∽△CO2E.
解:(1)补充完整图形如图9-7(3),三条
线段AC、CD、AD相等.
(2)结论:△ACD是正三角形.
证明:连结AO1、AO2、BO2、O1O2.
∵⊙O1、⊙O2是等圆,且⊙O1过O2点,
∴A O2= O1O2=A O1. ∴ ∠AO2 O1=600, ∴∠AO2B=1200.
∴ ∠D=![]() ∠AO2B=
∠AO2B=![]() ×1200=600. ∵∠ACB=∠AO2B=1200,
×1200=600. ∵∠ACB=∠AO2B=1200,
![]() ∴∠ACD=600. ∴△ACD是正三角形.
∴∠ACD=600. ∴△ACD是正三角形.
(3)(如图9-7(2))∵C是BO2的中点, ∴∠C O1O2=300. ∵∠ACO2=300.
∴
∠C O1O2=∠ACO2∵∠O1O2C=∠CO2E ∴
△O1O2C∽△CO2E. ∴![]() =
=![]() .
.
∵O1O2=O1C, ∴∠O1O2 C =∠O1CO2=∠CEO2 ∴CO2=CE. ∴CE2= O1O2·E O2.
说明:本例是一道以相交两圆为背景,集操作、测量、猜想、证明于一体探究性问题,着重考查动手操作变换图形和推理论证的能力.本例以留空回填命题的思路,解答时应顺向逐层进行.
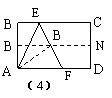
例6取一张矩形的纸进行折叠,具体操作过程如下:
第一步:先把矩形ABCD对折,折痕为MN,如图9-8(1);
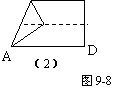
第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B′,
得Rt△A B′E,如图9-8(2);
第三步:沿E B′线折叠得折痕EF,如图9-8(3).
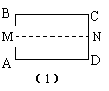
利用展开图9-8(4)探究:
(1) △AEF是什么三角形?证明你的结论.
(2) 对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.
 | |||
| |||
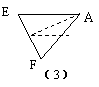
|
|
|
|
| |||||||
| |||||||
| |||||||
| |||||||
(2003年山西省中考试题)
分析:(1)经过操作测量易判定△AEF是正三角形.再运用平行线等分线段定理、直角三角形的性质来证明△AEF是正三角形;
(2) 不一定.运用由特殊到一般的思路来解答:若矩形恰好能折出等边三角形,先找出矩形长a与宽b的关系,再按b≤![]() a、
a、![]() a<b<a的情形分类讨论.
a<b<a的情形分类讨论.
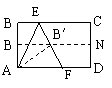
|
|
证法一:(如图右图)由平行线等分线段定理知:PE=PA,
∴B′P是Rt△A B′E斜边上的中线, ∴PA=P B′,∠1=∠3. 又∵PN//AD,
∴∠2=∠3.而∠BAF=2∠1+∠2=900, ∴∠1=∠2=300. ∴在Rt△A B′E,∠1+∠AEF=900,
∴∠AEF=600,∠EAF=∠1+∠2=600,∴△AEF是正三角形.
证法二:∵△ABE与△A B′E完全重合, ∴△ABE≌△A B′E,∠BAE=∠1.
由平行线等分线段定理知 ∴EB′=B′F. 又∠A B′E=900,∴△AB′E≌△A B′F,
AE=AF. ∴∠1=∠2=![]() ∠BAD=300.∴△AEF是正三角形.
∠BAD=300.∴△AEF是正三角形.
(2)不一定.
由上推证可知当矩形的长恰好等于△AEF的边AF时,即 矩形的宽:长AB:AF=sin600=![]() :2时正好能折出. 如果设矩形的长为a,宽为b ,可知当b≤
:2时正好能折出. 如果设矩形的长为a,宽为b ,可知当b≤![]() a时,按此法一定能折出等边三角形;当
a时,按此法一定能折出等边三角形;当![]() a<b<a时,按此法无法折出完整的等边三角形.
a<b<a时,按此法无法折出完整的等边三角形.
说明:折叠图形问题,着重考察动手操作和分析推理能力、图形的直觉判断能力和书面表述的数学素养等. 折叠图形的常见类型:对角线折叠问题;角平分线折叠问题;轴对称折叠问题;两点重合折叠问题等. 想一想本例属于哪种折叠问题?
例7 OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y 轴上,OA=10,OC=6.
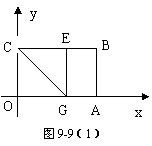
(1)如图9-9(1),在OA上选取一点G,将△COG沿CG翻折,使点O落在BC边上,记为E,求折痕CG所在直线的解析式.
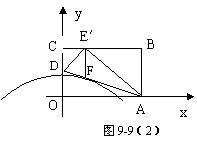
(2)如图9-9(2),在OC上选取一点D,将△AOD沿AD翻折,使点O落在BC边上,记为 E′. ①求折痕AD所在直线的解析式.
②再作E′F//AB,交AD于点F,若抛物线y=-![]() x2+h过点F,求此抛物线的解析式,并判断它与直线AD的交点的个数.
x2+h过点F,求此抛物线的解析式,并判断它与直线AD的交点的个数.
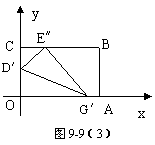
 (3)如图9-9(3),一般地,在OC、OA上选取适当的点D′、G′,使纸片沿D′G′翻折后,点O落在BC边上,记为E〞. 请你猜想:折痕D′G′所在直线与②中的抛物线会有什么关系?用(1)中的情形验证你的猜想.
(3)如图9-9(3),一般地,在OC、OA上选取适当的点D′、G′,使纸片沿D′G′翻折后,点O落在BC边上,记为E〞. 请你猜想:折痕D′G′所在直线与②中的抛物线会有什么关系?用(1)中的情形验证你的猜想.
 |
(2003年江苏省苏州市中考试题)
分析:(1)由折法易知:G(6,0)、C(0,6).
求得折痕CG的解析式为y=-x+6;
(2)①由勾股定理易求得D E′=![]() ,则折痕AD的
,则折痕AD的
解析式为:y=-![]() x+
x+![]() ;
;
②由题意设F(2,yF),点F在AD上,∴F的坐标为(2,![]() ),求出抛物线为y=-
),求出抛物线为y=-![]() x2+3. 再联立方程组,判定直线AD与抛物线只有一个交点.
x2+3. 再联立方程组,判定直线AD与抛物线只有一个交点.
解:(1)由折法知,四边形OCEG是正方形,∴OG=OC=6,∴G(6,0)、C(0,6).设直线CG的解析式为:y=kx+b,则0=6k+b, 6=0+b. ∴k=-1,b=6
∴直线CG的解析式为:y=-x+6.
(2) ①在Rt△ABE′中,BE′=![]() =8,∴CE′=2. 设OD=s,则DE′=s,
=8,∴CE′=2. 设OD=s,则DE′=s,
CD=6-s,∴在Rt△DCE′中,s2=(6-s)2+22, s=![]() .则D(0,
.则D(0,![]() ).
).
设AD:y=k′x+![]() .由于它过A(10,0),∴k′=-
.由于它过A(10,0),∴k′=-![]() . ∴AD:y=-
. ∴AD:y=-![]() x+
x+![]() .
.
②∵E′F//AB, ∴E′(2,6) ,∴设F(2,yF),∵F在AD上,∴yF=-![]() ×2+
×2+![]() =
=![]() ,
,
∴F(2,![]() ).又F在抛物线上,∴
).又F在抛物线上,∴![]() =-
=-![]() ×22+h. ∴抛物线的解析式为:y=-
×22+h. ∴抛物线的解析式为:y=-![]() x2+3.
x2+3.
将y=-![]() x+
x+![]() 代入y=-
代入y=-![]() x2+3. 得-
x2+3. 得-![]() x2+
x2+![]() x-
x-![]() =0. ∵△=(
=0. ∵△=(![]() )2-4×(-
)2-4×(-![]() )×(-
)×(-![]() )=0. ∴直线AD与抛物线只一个交点.
)=0. ∴直线AD与抛物线只一个交点.
(3)
例如可以猜想:折痕所在直线与抛物线y=-![]() x2+3只有一个交点;验证:在图1 中折痕为CG. 将y=-x+6 代入y=-
x2+3只有一个交点;验证:在图1 中折痕为CG. 将y=-x+6 代入y=-![]() x2+3.得-
x2+3.得-![]() x2+x-3=0.
x2+x-3=0.
∵△=1-4 (-3)×(-![]() )=0, ∴折痕CG所在直线的确与抛物线y=-
)=0, ∴折痕CG所在直线的确与抛物线y=-![]() x2+3只有一个交点.
x2+3只有一个交点.
说明:本例在直角坐标系中,以轴对称折叠为变化情境,探究折痕的动态变化,引其函数变化,并用特殊的(1)中的情形加以验证.若不用(1)中的情形验证,请猜想:D′G′所在直线与②中的抛物线会有什么位置关系?
【习题9】
1. 只利用一把有刻度的直尺,用度量的方法,按下列要求画图:
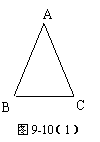
(1)在图9-10(1)中用下面的方法画等腰三角形ABC的对称轴:
①量出底边BC的长度,将线段BC二等分,即画出BC的中点D;
②画直线AD,即画出等腰三角形ABC的对称轴.
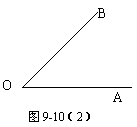
(2)在图9-10(2) 中画出∠AOB的对称轴,并写出画图和方法.
 | |||
 | |||
(2003年江苏省南京市中考试题)
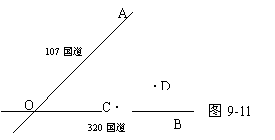 2.如图9-11,107国道OA和国道OB在我市相交于O点,在∠AOB的内部有工厂C和D,现要修建一个货站P,使P到OA、OB的距离相等且PC=PD,用尺规作货站P的位置(不写作法,保留作图痕迹,写出结论).
2.如图9-11,107国道OA和国道OB在我市相交于O点,在∠AOB的内部有工厂C和D,现要修建一个货站P,使P到OA、OB的距离相等且PC=PD,用尺规作货站P的位置(不写作法,保留作图痕迹,写出结论).
(2003年湖南省湘谭市中考试题)
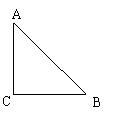
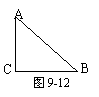 3.一服装厂里有大量形状为等腰直角三角形的边角布料(如图9-12),现找出其中的一种,测得∠C=900,AB=BC=4.今要从这种三角形中剪出一种扇形, 做成不同形状的玩具,使扇形的边缘半径恰好都在△ABC的边上,且扇形的弧与△ABC的其他边相切,请设计出所有可能符合题意的方案示意图,并求出扇形的半径(只要求画出图形,并直接写出扇形半径).
3.一服装厂里有大量形状为等腰直角三角形的边角布料(如图9-12),现找出其中的一种,测得∠C=900,AB=BC=4.今要从这种三角形中剪出一种扇形, 做成不同形状的玩具,使扇形的边缘半径恰好都在△ABC的边上,且扇形的弧与△ABC的其他边相切,请设计出所有可能符合题意的方案示意图,并求出扇形的半径(只要求画出图形,并直接写出扇形半径).
(2002年湖北省黄冈市中考试题)
4. 如图9-13,有两个正方形的花坛,准备把每个花坛都分成形状相同的四块,种不同的花草.下面左边的两个图案是设计示例,请你在右面的两个正方形中设计两个不同的图案.
示例: 请你设计:
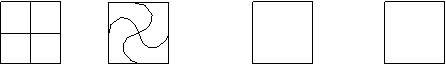 |
图9-13 (2003年江苏省苏州市中考试题)
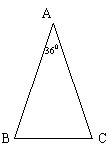
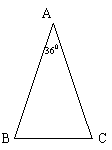
5. 已知,如图9-14,△ABC中,AB=AC,∠A=360.
仿照图(a),请你再设计两种不同的分法,将△ABC分割成3个三角形,使得每个三角形都是等腰三角形. (图(b)、图(c)供画图用,作图工具不限,不要求写出画法,不要求证明;要求标出所分得的每个等腰三角形三个内角的度数). (2003年江苏省镇江市中考试题)
 |  | ||||
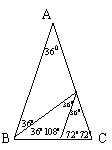 | |||||
| |
图9-14
如图9-15,把一个边长为2cm的的正方形剪成四个全等的直角三角形. 请用这四个直角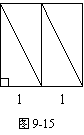 三角形拼成符合下列要求的图形(全部用上,互不
三角形拼成符合下列要求的图形(全部用上,互不
重叠且不留空隙),并把你的拼法仿照右图按实际大
小画在方格纸内(方格为1cm×1cm).
(1)不是正方形的菱形(一个);(2)不是正方形的矩形(一个).
(3)梯形(一个). (4)不是矩形和菱形的平行四边形(一个)
(5)不是梯形和平行四边形的凸四边形(一个).
7.已知,AB为⊙O的直径,P为AB延长上的一个动点,过点P作⊙O的切线,设切点为C.
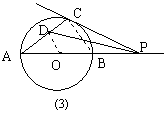
(1) 当点P在AB延长线上,如图9-16(1)时,连结AC,作∠APC的平分线,交AC于D,请你测量∠CDP的度数.
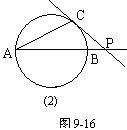
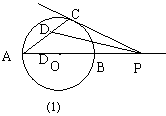
(2) 当点P在AB延长线上,如图9-16(2)和(3)所示时,连结AC,请你分别在这两个圆中用尺规作∠APC的平分线(不写作法,保留痕迹),设此角平分线交AC于点D,然后在这两个图中分别测量出∠CDP的度数.
猜想:∠CDP的度数是否随点P在AB延长线上位置的变化而变化?请对你加以证明.
 | |||||
 | |||||
 | |||||
(2002年北京市要城区中考试题)
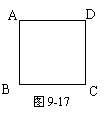 8. 操作:如图9-17,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角尺的直角顶点与P重合,并且一条直角边始终经过点B,另一直角边与正方形的某一边所在直线交于点E.探究:(1)观察操作结果,哪一个三角
8. 操作:如图9-17,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角尺的直角顶点与P重合,并且一条直角边始终经过点B,另一直角边与正方形的某一边所在直线交于点E.探究:(1)观察操作结果,哪一个三角
形与△BPC相似?并证明你的结论;
(2)当点P位于CD的中点时,你找到的三角形与
△BPC的周长比是多少? (2003年云南省昆明市中考试题)
【习题9】参考答案
1.(1)略;(2)画图略.画图方法:①利用有刻度的直尺,在∠AOB的边OA、OB上分别截取OC、OD,使OC=OD. ②连结CD,量出CD的长,将线段CD二等分,画出线段CD的中点E. ③画直线OE.直线OE即为∠AOB的对称轴.
2. 画图略.提示:作∠AOB的平分线OP,再作CD的垂直平分线PQ与OP相交于点P.
∴点P就是货站的位置.
3. 
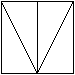
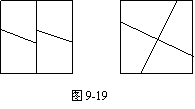
 通过观察、分析,符合题目要求的方案可以设计出如图9-19所示的四种方案.
通过观察、分析,符合题目要求的方案可以设计出如图9-19所示的四种方案.
| |||||||||||
| |||||||||||
 | |||||||||||
| |||||||||||
| |||||||||||
4.(任选图9-19中两个图案,答案不惟一.)
 | |||||
 | |||||
 | |||||
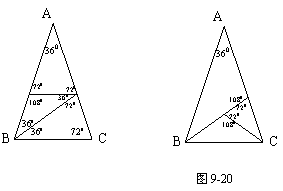
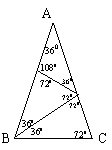 5.本题答案有多种,这里图9-20提供了3种参考答案.如果学生画出的两个图形是同一类型的对称图形视为正确,若学生画出(1)的对称图形也视为正确.
5.本题答案有多种,这里图9-20提供了3种参考答案.如果学生画出的两个图形是同一类型的对称图形视为正确,若学生画出(1)的对称图形也视为正确.
| |
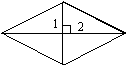
![]() 6.(1)
(2)
6.(1)
(2)
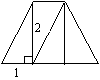 (3)
(3)
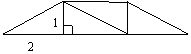
(两个图形任画一个)
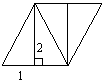 (4)
(4)
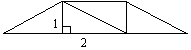 | |||||
(四个图形任画一个)
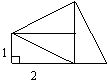
 (5)
(5)
(两个图形任画一个)
7. (1)测量结果:∠CDP=450.(2)作图略,题图中测量结果均为∠CDP=450.猜想:∠CDP=450为确定值,∠CDP的度数不随点P在AB的延长线上位置的变化而变化.
(3)证明 如图9-16(3),连结CB,∵AB为⊙O的直径,∴∠ACB=900,∴∠A+∠ABC=900又PC为⊙O的切线,∴∠A=∠PCB.又∵PD平分∠APC,∴∠BPD=∠CPD.又∵∠ABC=∠APC+∠PCB,∴2∠A+2∠BPD=900. ∠CDP=∠A+∠BPD=450.
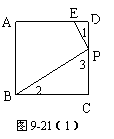
8. 解:(1)如图9-21(1),另一条直角边与AD交于点,则△PDE∽△BCP.
 | |||||||
 | |||||||
 | |||||||
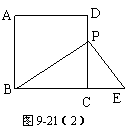 | |||||||
证明:在△PCE和△BCP中,∵∠1+∠3=900 ∠2+∠3=900 ∴∠1=∠2
又∠PDE=∠BCP=900∴△PCE∽△BCP.或如图9-21(2),若一条直角边与BC的延长线交于点E,同理可证△BPE∽△BCP.
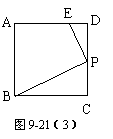
(2)如图9-21(3),当点P位于CD的中点时,若另一条直角边与AD交于点E,则![]() =
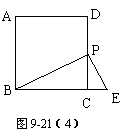
=![]() 又∵△PDE∽△BCP∴△PDE和△BCP的周长比是1:2. 或:如图9-21(4),若另一条直角边与BC的延长线交于点E,同理可证△PCE与△BCP的周长是1:2,或若另一条直角边与BC的延长线交于点E∵
又∵△PDE∽△BCP∴△PDE和△BCP的周长比是1:2. 或:如图9-21(4),若另一条直角边与BC的延长线交于点E,同理可证△PCE与△BCP的周长是1:2,或若另一条直角边与BC的延长线交于点E∵![]() =
=![]() ,又△BPE∽△BCP,
,又△BPE∽△BCP,
∴△PCE与△BCP的周长比是![]() :2.
:2.