德州市2006年中等学校招生考试(课标卷)
数学试题
注意事项:
1.本试题分第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷3页为选择题,24分;第Ⅱ卷8页为非选择题,96分;全卷共11页,满分120分,考试时间为120分钟.
2.答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目涂写在答题卡上,考试结束,试题和答题卡一并收回.
3.第Ⅰ卷每题选出答案后,必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑,如需改动,先用橡皮擦干净,再改涂其它答案.
4.考试时,允许使用科学计算器.
第Ⅰ卷(选择题 共24分)
一、选择题(本大题共8小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.)
1.气象台预报“本市明天降水概率是80%”,对此信息,下面的几种说法正确的是( )
A.本市明天将有80%的地区降水 B.本市明天将有80%的时间降水
C.明天肯定下雨 D.明天降水的可能性比较大
2.若反比例函数![]() 的图象经过点
的图象经过点![]() ,则这个函数的图象一定经过点( )
,则这个函数的图象一定经过点( )
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
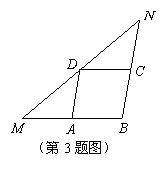
3.在![]() 中,
中,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别在
分别在![]() ,
,![]() ,
, ![]() 上,四边形
上,四边形![]() 为平行四边形,且
为平行四边形,且![]() , 则
, 则![]() 的周长是( )
的周长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.由几个小立方体搭成的一个几何体如图1所示,它的主(正)视图见图2,那么它的俯视图为( )
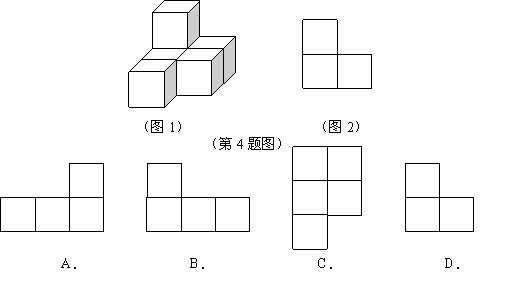 |
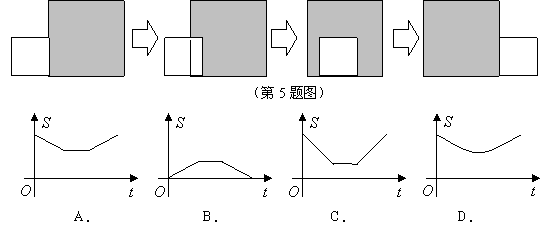
5.如图所示:边长分别为![]() 和
和![]() 的两个正方形,其一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为
的两个正方形,其一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为![]() ,大正方形内除去小正方形部分的面积为
,大正方形内除去小正方形部分的面积为![]() (阴影部分),那么
(阴影部分),那么![]() 与
与![]() 的大致图象应为( )
的大致图象应为( )
 |
 6.某时刻两根木棒在同一平面内的影子如图所示,此时,第三根木棒的影子表示正确的是( )
6.某时刻两根木棒在同一平面内的影子如图所示,此时,第三根木棒的影子表示正确的是( )
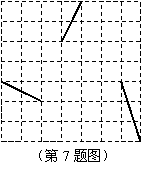
7.如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动( )
A.![]() 格 B.
格 B.![]() 格 C.
格 C.![]() 格 D.
格 D.![]() 格
格
 |
8.已知点![]() ,
,![]() ,
,![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,则直线
,则直线![]() 对应的函数表达式是( )
对应的函数表达式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共96分)
注意事项:
1.第Ⅱ卷共8页,用钢笔或圆珠笔直接写在试卷上.
2.答卷前将密封线内的项目填写清楚.
二、填空题(本大题共8小题,共24分,只要求填写最后结果,每小题填对得3分).
9.随着中国综合国力的提升,近年来全球学习汉语的人数不断增加.据报道,2005年海外学习汉语的学生人数已达![]() 人,用科学记数法表示为_____________人(保留3个有效数字).
人,用科学记数法表示为_____________人(保留3个有效数字).
10.从两副拿掉大、小王的扑克牌中,各抽取一张,两张牌都是红桃的概率是_____________.
11.钟表的轴心到分针针端的长为![]() ,那么经过
,那么经过![]() 分钟,分针针端转过的弧长是_____________.
分钟,分针针端转过的弧长是_____________.
12.已知方程组![]() 的解为
的解为![]() ,则
,则![]() 的值为_____________.
的值为_____________.
13.将点![]() 绕原点
绕原点![]() 顺时针旋转
顺时针旋转![]() 到点
到点![]() ,则点
,则点![]() 的坐标是_____________.
的坐标是_____________.
14.如图:已知![]() 中,
中,![]() ,
,![]() ,直角
,直角![]() 的顶点
的顶点![]() 是
是![]() 中点,两边
中点,两边![]() ,
,![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,给出以下五个结论:
,给出以下五个结论:
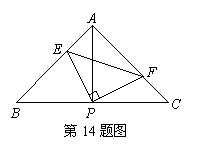 ①
①![]() ②
②![]() ③
③![]() 是等腰直角三角形④
是等腰直角三角形④![]() ⑤
⑤![]() .当
.当![]() 在
在![]() 内绕顶点
内绕顶点![]() 旋转时(点
旋转时(点![]() 不与
不与![]() ,
,![]() 重合),上述结论中始终正确的序号有______________.
重合),上述结论中始终正确的序号有______________.
15.要在一个矩形纸片上画出半径分别是![]() 和
和![]() 的两个外切圆,该矩形面积的最小值是______________.
的两个外切圆,该矩形面积的最小值是______________.
16.如图,已知![]() 的面积
的面积![]() .
.
在图(1)中,若![]() ,则
,则![]() ;
;
在图(2)中,若![]() ,则
,则![]() ;
;
在图(3)中,若![]() ,则
,则![]() ;
;
按此规律,若![]() ,则
,则![]() .
.

三、解答题(本大题共7小题,共72分.解答要写出必要的文字说明、证明过程或演算步骤.)
17.(本题满分6分)
解不等式组,并把其解集在数轴上表示出来:
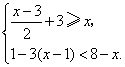
18.(本题满分10分)
 某单位欲从内部招聘管理人员一名,对甲、乙、丙三名侯选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
某单位欲从内部招聘管理人员一名,对甲、乙、丙三名侯选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
| 测试项目 | 测试成绩分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 75 | 80 | 90 |
| 面试 | 93 | 70 | 68 |
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如上图所示,每得一票记作1分.
(1)请算出三人的民主评议得分;
(2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到![]() )?
)?
(3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按![]() 的比例确定个人成绩,那么谁将被录用?
的比例确定个人成绩,那么谁将被录用?
19.(本题满分10分)
近年来,由于受国际石油市场的影响,汽油价格不断上涨,请你根据下面的信息,帮小明计算今年5月份每升汽油的价格.
 |
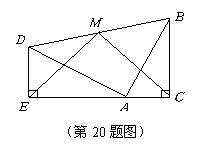
20(本题满分10分)
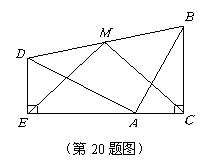 两个全等的含
两个全等的含![]() ,
,![]() 角的三角板
角的三角板![]() 和三角板
和三角板![]() 如图所示放置,
如图所示放置,![]() ,
,![]() ,
,![]() 三点在一条直线上,连结
三点在一条直线上,连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,试判断
,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
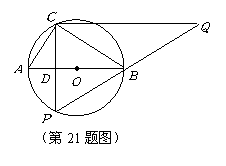
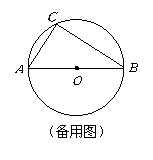
21.(本题满分12分)
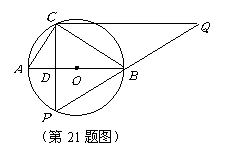
半径为![]() 的
的![]() 中,直径
中,直径![]() 的不同侧有定点
的不同侧有定点![]() 和动点
和动点![]() ,已知
,已知![]() ,点
,点![]() 在
在![]() 上运动,过点
上运动,过点![]() 作
作![]() 的垂线,与
的垂线,与![]() 的延长线交于点
的延长线交于点![]() .
.
 (1)当点
(1)当点![]() 运动到与点
运动到与点![]() 关于直径
关于直径![]() 对称时,求
对称时,求![]() 的长;
的长;
 (2)当点
(2)当点![]() 运动到什么位置时,
运动到什么位置时,![]() 取到最大值,并求出此时
取到最大值,并求出此时![]() 的长.
的长.
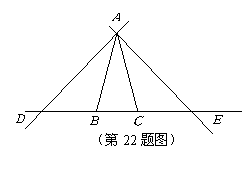
22.(本题满分12分)
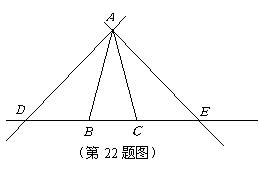
如图,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 上运动,设
上运动,设![]() ,
,![]() .
.
(1)如果![]() ,
,![]() ,试确定
,试确定![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果![]() 的度数为
的度数为![]() ,
,![]() 的度数为
的度数为![]() ,当
,当![]() 满足怎样的关系式时,(1)中
满足怎样的关系式时,(1)中![]() 与
与![]() 之间的函数关系式还成立,试说明理由.
之间的函数关系式还成立,试说明理由.
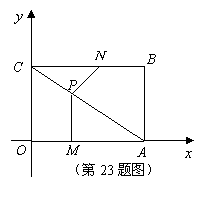
23.(本题满分12分)
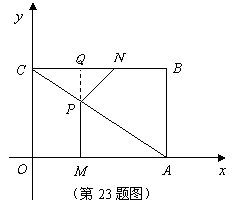
如图,平面直角坐标系中,四边形![]() 为矩形,点
为矩形,点![]() 的坐标分别为
的坐标分别为![]() ,动点
,动点![]() 分别从
分别从![]() 同时出发,以每秒1个单位的速度运动.其中,点
同时出发,以每秒1个单位的速度运动.其中,点![]() 沿
沿![]() 向终点
向终点![]() 运动,点
运动,点![]() 沿
沿![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,连结
,连结![]() ,已知动点运动了
,已知动点运动了![]() 秒.
秒.
(1)![]() 点的坐标为( , )(用含
点的坐标为( , )(用含![]() 的代数式表示);
的代数式表示);
(2)试求![]() 面积
面积![]() 的表达式,并求出面积
的表达式,并求出面积![]() 的最大值及相应的
的最大值及相应的![]() 值;
值;
(3)当![]() 为何值时,
为何值时,![]() 是一个等腰三角形?简要说明理由.
是一个等腰三角形?简要说明理由.
 |
德州市2006年中等学校招生考试(课标卷)
数学试题参考解答及评分意见
评卷说明:
1.选择题和填空题中的每小题,只有满分和零分两个评分档,不给中间分.
2.解答题每小题的解答中所对应的分数,是指考生正确解答到该步骤所应得的累计分数,每小题只给出一种解法,对考生的其他解法,请参照评分意见进行评分.
3.如果考生在解答的中间过程出现计算错误,但并没有改变试题的实质和难度,其后续部分酌情给分,但最多不超过正确解答分数的一半;若出现严重的逻辑错误,后续部分就不再给分.
一、选择题(本大题共8小题,每小题3分,共24分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | D | C | D | C | A | D | B | D |
二、填空题(本大题共8小题,每小题3分,共24分)
9.![]() 10.
10.![]() 11.
11.![]() 12.6 13.
12.6 13.![]()
14.①②③⑤ 15.![]() 16.
16.![]()
三、解答题(本大题共7小题,共72分)
17.(本小题满分6分)
解:解不等式![]() ,得
,得![]() ,····································································· 2分
,····································································· 2分
解不等式![]() ,得
,得![]() .···································································· 4分
.···································································· 4分
所以,原不等式组的解集是![]() .···································································· 5分
.···································································· 5分
在数轴上表示为
![]() ·································· 6分
·································· 6分
18.(本小题满分10分)
解:(1)甲、乙、丙的民主评议得分分别为:50分,80分,70分.···························· 3分
(2)甲的平均成绩为:![]() (分),
(分),
乙的平均成绩为:![]() (分),
(分),
丙的平均成绩为:![]() (分).
(分).
由于![]() ,所以候选人乙将被录用.············································· 6分
,所以候选人乙将被录用.············································· 6分
(3)如果将笔试、面试、民主评议三项测试得分按![]() 的比例确定个人成绩,那么
的比例确定个人成绩,那么
甲的个人成绩为:![]() (分),
(分),
乙的个人成绩为:![]() (分),
(分),
丙的个人成绩为:![]() (分),
(分),
由于丙的个人成绩最高,所以候选人丙将被录用.················································ 10分
19.(本小题满分10分)
解:设去年5月份汽油价格为![]() 元/升,则今年5月份的汽油价格为
元/升,则今年5月份的汽油价格为![]() 元/升,··········· 1分
元/升,··········· 1分
根据题意,得![]() .············································································· 5分
.············································································· 5分
整理,得![]() .
.
解这个方程,得![]() .······························································································· 8分
.······························································································· 8分
经检验,![]() 是原方程的解.····················································································· 9分
是原方程的解.····················································································· 9分
所以![]() .
.
答:今年5月份的汽油价格为![]() 元/升.····································································· 10分
元/升.····································································· 10分
20.(本小题满分10分)
解:![]() 的形状是等腰直角三角形.····································································· 1分
的形状是等腰直角三角形.····································································· 1分
 证明:连接
证明:连接![]() ,由题意得:
,由题意得:
![]() .
.
![]() ………………2分
………………2分
又![]() ,
,
![]() .
.
![]() .
.
![]() .······························································································ 5分
.······························································································ 5分
![]() .············································································· 7分
.············································································· 7分
又![]() ,
,
![]() .
.
![]() .··········································································································· 9分
.··········································································································· 9分
所以![]() 的形状是等腰直角三角形.····································································· 10分
的形状是等腰直角三角形.····································································· 10分
21.(本小题满分12分)
解:(1)当点![]() 运动到与点
运动到与点![]() 关于直径
关于直径![]() 对称时,如图所示,此时
对称时,如图所示,此时![]() 于
于![]() ,
,
 又
又![]() 为
为![]() 的直径,
的直径,
![]() .
.
![]() ,
,
![]() .
.
又![]() ,
,
![]() .…………………4分
.…………………4分
在![]() 和
和![]() 中,
中,
![]() ,
,
![]() ,
,
![]() .······················································································· 6分
.······················································································· 6分
![]() .··························································· 8分
.··························································· 8分
(2)因为点![]() 在弧
在弧![]() 上运动过程中,有
上运动过程中,有![]() ,
,
所以![]() 最大时,
最大时,![]() 取到最大值.············································································· 10分
取到最大值.············································································· 10分
![]() 当
当![]() 过圆心
过圆心![]() ,即
,即![]() 取最大值5时,
取最大值5时,![]() 最大,最大为
最大,最大为![]() .···························· 12分
.···························· 12分
22.(本小题满分12分)
解:(1)在![]() 中,
中,![]() ,
,
![]() ,…………………………1分
,…………………………1分
![]() .
.
又![]() ,
,
![]() .…………………………2分
.…………………………2分
又![]() ,
,
![]() .·································································································· 3分
.·································································································· 3分
![]() .································································································· 4分
.································································································· 4分
![]() .············································································································ 5分
.············································································································ 5分
即![]() ,所以
,所以![]() .····························································································· 7分
.····························································································· 7分
(2)当![]() 满足关系式
满足关系式![]() 时,函数关系式
时,函数关系式![]() 仍然成立.···················· 8分
仍然成立.···················· 8分
此时,![]() .·············································································· 9分
.·············································································· 9分
又![]() ,
,
![]() .·································································································· 10分
.·································································································· 10分
又![]() 仍然成立.················································ 11分
仍然成立.················································ 11分
从而(1)中函数关系式![]() 成立.··········································································· 12分
成立.··········································································· 12分
23.(本小题满分12分)
解:(1)由题意可知,![]() ,
,![]() ,
,
![]() 点坐标为
点坐标为![]() .························································································ 2分
.························································································ 2分
(2)设![]() 的面积为
的面积为![]() ,在
,在![]() 中,
中,![]() ,
,![]() 边上的高为
边上的高为![]() ,其中
,其中![]() . 3分
. 3分
![]() .············································· 5分
.············································· 5分
![]() 的最大值为
的最大值为![]() ,此时
,此时![]() .················································································ 7分
.················································································ 7分
(3)延长![]() 交
交![]() 于
于![]() ,则有
,则有![]() .
.
 ①若
①若![]() ,
,
![]() .
.
![]() ,
,
![]() .……………………………………9分
.……………………………………9分
②若![]() ,则
,则![]() ,
,
![]() .································································································ 10分
.································································································ 10分
③若![]() ,则
,则![]() .
.
![]() ,
,
![]() 在
在![]() 中,
中,![]() .
.
![]() ,
,![]() .····························································· 11分
.····························································· 11分
综上所述,![]() ,或
,或![]() ,或
,或![]() .
.