江西省2006年中等学校招生考试
数学试卷（大纲版）
说明：本卷共有六个大题，25个小题，全卷满分120分，考试时间120分钟。
一、
填空题（本大题共10小题，每小题3分，共30分）
1、计算“2-3＝___________。
2、若m、n互为相反数，则m+n=_________.
3、在△ABC中，∠A＝80°，∠B＝60°，则∠C＝_________.
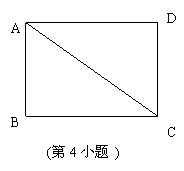
4、如图，在矩形ABCD中，AB＝1，BC＝2则AC＝___________.
5、当m<3时，
=___________.
6、若圆柱的底面半径2cm,，高为3cm，则它的侧面积是___________。
7、近视眼镜的度数y（度）与镜片焦距x(m)成反比例，已知400度的近视眼镜镜片的焦距为0.25m，则y与x的函数关系式为__________________。
8、方程
的解是_______________________。
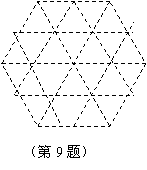9、请在由边长为1的小正三角形组成的虚线网格中，画一个所有顶点均在格点上，且至少有一条边为无理数的等腰三角形。
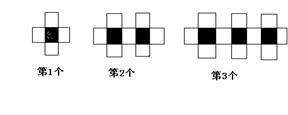
10、用黑白两种颜色的正方形纸片，按黑色纸片数逐渐加1的 规律拼成一列图案：
……
（1）第4个图案中有白色纸片________张；
（2）第n个图案台有白色纸片________张。
二、选择题（本大题共有6小题，每题3分，共18分），每小题只有一个正确选项，请把正确选项的代号填在题后的括号内。
11、下列运算正确的是（ ）
A、a+a=2a2 B、a2·a＝2 a2 C、（2a）2÷a=4a D、（－ab）2=ab2
12、在平面直角坐标系中，点（－3,2）在（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
13、计算
的结果为（ ）
A、
B、3 C、3 D、9
14、下列图案都是由字母“m”经过变形、组合而成的，其中不是中心对称图形的是（ ）
?
15、某公司2003年缴税60万元，2005年缴税80万元，设该公司这两年缴税的年平均增长率为x,则得到方程（ ）
A、60＋2x=80 B、60（x＋1）＝80
C、60x
＝80 D、60(x+1)=80
16、如图，身高为1.6米的某学生想测学校旗杆的高度，当他站在C处时，他头顶端的影子重合，并测得AC＝2.0米，BC＝8.0米，则旗杆的高度是（ ）
A、6.4米 B、7.0米 C、8.0米 D、9.0米
三、（本大题共3小题，第17小题6分，第18、19小题各7分，共20分）
17、计算：（x-y）-(y+2x)(y-2x);
18、已知关于x的一元二次方程x+kx-1=0 ,(1)求证：方程有两个不相等的实数根； （2）设方程的两根分别为x
,x
,且满足x＋x＝x·x，求k的值。
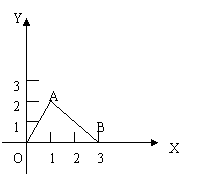
19、如图，在平面直角坐标系中，点A在第一象限，点B的坐标为（3,0），OA＝2，∠AOB＝60º。（1）求点A的坐标；（2）若直线AB交y轴于点C，求△AOC的面积。
 |
20、如图，AB是⊙0的直径，BC是弦，OD⊥BC于E，交
于D。
（1）请写出四个不同类型的正确结论；
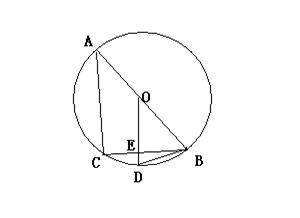（2）连结CD，设∠CDB＝α，∠ABC＝β，试找出α与β之间的一种关系式，并予以证明。
21、如图，在梯形ABCD中，AD∥BC，AD>CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C
处，折痕DE交BC于点E，连结CE。
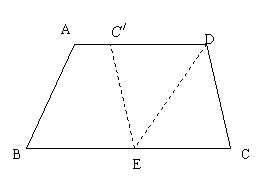（1）求证：四边形CD CE是菱形；
（2）若BC＝CD＋AD，试判断四边形ABED的形状，并加以证明
。
五、（本大题共有2小题，第22小题8分，第23小题9分，共17分）
22、一次期中考试中，A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示：（单位：分）
| A | B | C | D | E | 平均分 | 标准差 | |
| 数学 | 71 | 72 | 69 | 68 | 70 |
| |
| 英语 | 88 | 82 | 94 | 85 | 76 | 85 |
（1）求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差；
（2）为了比较不同学科考试成绩的好与差，采用标准分是一个合理的选择，标准分的计算公式是：标准分＝（个人成绩－平均成绩）÷成绩标准差。
从标准分看，标准分大的考试成绩更好。请问A同学在本次考试中，数学与英语哪个学科考得更好？
友情提示：一组数据的标准差计算公式是S＝
，其中
为n个数据
、
…
r的平均数。
23、小杰到学校食堂买饭，看到A、B两窗口前面排队的人一样多（设为a人，a>8），就站在A窗口队伍的后面，过了2分钟，他发现A窗口每分钟有4人买了饭离开队伍上，B窗口每分钟有6人买了饭离开队伍，且B窗口队伍后面每分钟增加5人。
（1）此时，若小杰继续在A窗口排队，则他到达窗口所花的时间是多少（用含a的代数式表示）？
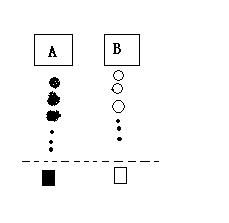（2）此时，若小杰迅速从A窗口队伍转移到B窗口后面重新排队，且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少，求a的取值范围（不考虑其它因素）。
六、（本大题共2小题，第24小题9分，第25小题10分，共19分）
24、一条抛物线y=
经过点（0，
（1）求这条抛物线的解析式，并写出它的顶点坐标坐标；
（2）现有一半径为1，圆心P在抛物线上运动的动圆，当⊙P与坐标轴相切时，求轴心P的坐标。
25、问题背景 某课外学习小组在一次学习研讨中，得到了如下两个命题：
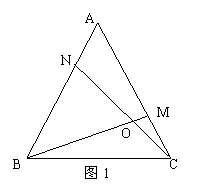
①如图1，在正三角形△ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON＝60º，则BM＝CN；
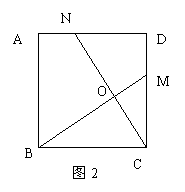
②如图2，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON＝90º，则BM＝CN；
然后运用类比的思想提出了如下命题：
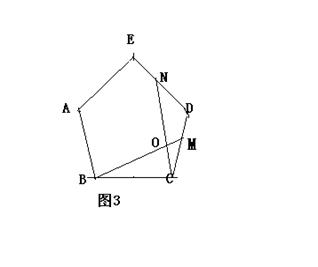
③如图3，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON＝108º，则BM＝CN。
任务要求：
（1）请你从①、②、③三个命题中选择一个进行证明；（说明：选①做对得4分，选②做对得3分，选③做对得5分）
(2)请你继续完成下列探索：
①请在图3中画出一条与CN相等的线段DH，使点H在正五边形的边上，且与CN相交所成的一个角是108º，这样的线段有几条？（不必写出画法，不要求证明）
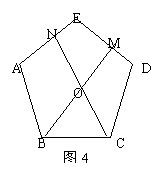
②如图4，在正五边形ABCDE中，M、N分别是DE、EA上的点，BM与CN相交于点O，若∠BON＝108º，请问结论BM＝CN是否还成立？若成立，请给予证明；若不成立，请说明理由。
 | |||
 | |||
