江西省南昌市2006年初中毕业暨中等学校招生考试
数 学 试 卷
说明:本卷共有五个大题,25个小题,全卷满分120分.考试时间120分钟
一、选择题(本大题共8小题,每小题3分,共24分)每小题只有一个正确选项,请把正确选项的代号填在题后的括号内
1. 下列四个运算中.结果最小的是 【 】
A 1+(-2) B 1-(-2) C l×(-2) D 1![]() (-2)
(-2)
2.在下列运算中,计算正确的是 【 】
A ![]() B
B ![]() C
C![]() D
D ![]()
3. 两圆半径分别为5和3,圆心距为8,则两圆的位置关系是 【 】
A内切 B相交 C外切 D外离
4.若点A(2、n)在x轴上则 点B(n-2 ,n+1)在 【 】
A第一象限 B第二象限 C第三象限 D第四象限
5.某运动场的面积为300m![]() ,则它的万分之一的面积大约相当于 【 】
,则它的万分之一的面积大约相当于 【 】
A课本封面的面积 B课桌桌面的面积
C黑板表面的面积 D教室地面的面积
6.某同学的身高为1.6米,某一时刻他在阳光下的影长为1.2米.与他相邻的一
棵树的影长为3. 6米,则这棵树的高度为 【 】
 A 5 .3米 B 4. 8米 C 4 .0米 D 2.7米
A 5 .3米 B 4. 8米 C 4 .0米 D 2.7米
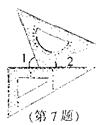
7. 一副三角扳按如图方式摆放,且∠1的度数比∠2的度数大50°,若设∠1=x°∠2=y°,则可得到方程组为 【 】
A![]() B
B ![]() C
C![]() D
D![]()
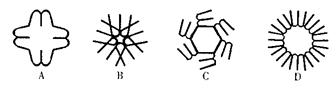
8.下列图案都是由宁母“m”经过变形、组合而成的.其中不是中心对称图形的是【 】
二、填空题(本大题共8小题,每小题3分.共24分)
9.分解因式![]()
10.计算:![]()
11.在△ABC中∠A=80°∠B=60° ,则∠C=
12.近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为
0. 25m,则y与x的函数是关系式为
 13.若分式
13.若分式![]() 的值为零,则x的值为
的值为零,则x的值为
14.若圆锥的母线长为3 cm,底面半径为2 cm,则圆锥的侧面展开图的面积
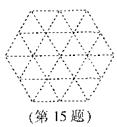
I5. 请在由边长为1的小正三角形组成的虚线网格中,画出1 个所有顶点均在格点上,且至少有一条边为无理数的等腰三角形
16用黑白两种颜色正方形的纸片按黑色纸片数逐渐加l的规律拼成一列图案:
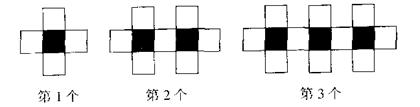
(1)第4个图案中有白色纸片 张
(2)第n个图案中有白色纸片 张
三、(本大题共4小题,每小题6分,共24分)
17 计算:![]()
18已知关于x的一元二次方程![]()
(I)求证方程有两个不相等的实数根:
(2)设的方程有两根分别为![]() 日满足
日满足![]() 求k的值
求k的值
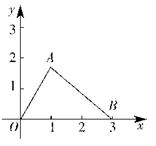
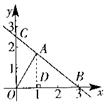
19如图,在平面直角坐标系中,点A在第一象限,点B的坐标为(3,0),OA=2,∠AOB=60°
 (I)
求点A的坐标:
(I)
求点A的坐标:
(2)若直线AB交x轴于点C,求△AOC的面积.
20 如图AB是⊙O的直径,BC是⊙O弦OD⊥CB于点E,交![]() 于点D
于点D
(1)请写出三个不同类型的正确结论:
(2)连结CD,设∠CDB=![]() ,∠ABC=
,∠ABC=![]() ,试找出
,试找出![]() 与
与![]() 之间的一种关系式并给予证明.
之间的一种关系式并给予证明.
四、(本大题共3小题.每小题8分.共24分)
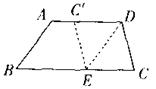
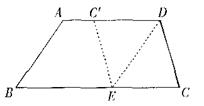 21.如图.在梯形纸片ABCD中.AD∥BC,AD>CD.将纸片沿过点D的直线折叠,使点C落在AD上的点
21.如图.在梯形纸片ABCD中.AD∥BC,AD>CD.将纸片沿过点D的直线折叠,使点C落在AD上的点![]() 处,折痕DE交BC于点E.连结
处,折痕DE交BC于点E.连结![]() E
E
(1)求证:四边形CD![]() E是菱形;
E是菱形;
(2)若BC=CD+AD,试判断四边形ABED的形状,并加以证明;
22一次期中考试中A、B、C、D、E五位同学的数学、英语成绩等有关信息、如下表所示:

(I)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的
计算公式是标准分=(个人成绩-平均成绩)÷成绩标准差
从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语
哪个学科考得更好.
友情提示:一组数据的标准差计算公式是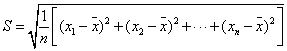
,其中 ![]() 为n个数据
为n个数据 ![]() 的平均数.
的平均数.
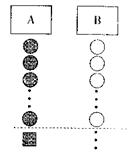 23小杰到学校食堂买饭,看到A、B两窗口前面排的人一样多(设为a人,a>8),就站到A窗口队伍的后面排队,过了 2分钟,他发现A窗口每分钟有4人买了饭离开队伍,B窗口每分钟有6人买了饭离开队伍,且B窗口队伍后面每分钟增加5人
23小杰到学校食堂买饭,看到A、B两窗口前面排的人一样多(设为a人,a>8),就站到A窗口队伍的后面排队,过了 2分钟,他发现A窗口每分钟有4人买了饭离开队伍,B窗口每分钟有6人买了饭离开队伍,且B窗口队伍后面每分钟增加5人
(1)此时,若小杰继续在A窗口排队.则他到达A窗口所花的时间是多少(用含a的代数式表示)
(2)此时,若小杰迅速从A窗口转移到B窗口队伍后面重新排队,且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少,求a的取值范围(不考虑其它因素).
五、(本大题共2小题,每小题12分.共24分)
24已知抛物线![]() ,经过点A(0,5)和点B(3 ,2)
,经过点A(0,5)和点B(3 ,2)
(1)求抛物线的解析式:
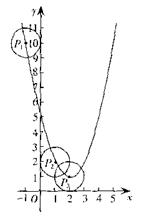
(2)现有一半径为l,圆心P在抛物线上运动的动圆,问⊙P在运动过程中,是否存在⊙P
与坐标轴相切的情况?若存在,请求出圆心P的坐标:若不存在,请说明理由;
(3)若⊙ Q的半径为r,点Q 在抛物线上、⊙Q与两坐轴都相切时求半径r的值
25问题背景;课外学习小组在一次学习研讨中,得到了如下两个命题:
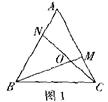
①如图1,在正三角形ABC中,M,N分别是AC、AB上的点,BM与CN相交于点O,若∠BON=60°.则BM=CN:
②如图2,在正方形ABCD中,M、N分别是CD、AD上的点.BM
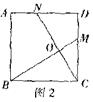 与CN相交于点O,若∠BON=90°.则BM=CN.
与CN相交于点O,若∠BON=90°.则BM=CN.
然后运用类似的思想提出了如下命题:
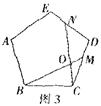
③如图3,在正五边形ABCDE中,M、N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.
任务要求
(1)请你从①.②,③三个命题中选择一个进行证明;
(说明:选①做对的得4分,选②做对的得3分,选③做对的得5分)
(2) 请你继续完成下面的探索;
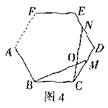 ①如图4,在正n(n≧3)边形ABCDEF
①如图4,在正n(n≧3)边形ABCDEF![]() 中,M,N分别是CD、DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立(不要求证明)
中,M,N分别是CD、DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立(不要求证明)
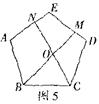
②如图5,在正五边形ABCDE中,M、N分别是DE,AE上的点,BM与CN相交于点O,∠BON=108°时,试问结论BM=CN是否还
成立,若成立,请给予证明.若不成立,请说明理由
 (I)我选 .
(I)我选 .
证明:
江西省南昌市2006年初中毕业暨中等学校招生考试
数学试题参考答案及评分意见说明
1、如果考生的解答与本参考答案不同,可根据试题的主要考查内容参照评分标准制定相应
的评分细则后评卷
2、每题都要评阅到底,不要因为考生的解答中出现错误而中断对题的评阅:当考生的解
答在某一步出现错误,影响了后继部分时,如果该步以后的解答未改变这题的内容和难度则
可视影响的程度决定后面部分的给分;但不得超过后面部分应给分数的一半:如果这一步以
后的解答有较严重的错误.就不给分 .
3、解答右端所注分数,表示考生正确做到这一步应得的累加分数
4、只给整数分数
一,选择题(本大题共8小题.每小题3分.共24分)
1. C;2. D,3. C;4 B;5. A;6. B;7. D;8. B
二、填空题(本大题共8小题,每小题3分.共24分)
9.a(a-b);10.![]() ;11.40°;12.
;11.40°;12. ![]() ;13.
1; 14 .6
;13.
1; 14 .6![]() :
:
15.本题答案不惟一,只要符合要求都给满分,以下答案供参考

16.(1)13;(2)3n+l
说明:1. 第12小题不写x>O.也给满分
2. 第16小题第(1)问1分,第(2)问2分
三、(本大题共4小题.每小题6分,共24分)-
17.解:原式=![]() … ……… 2分
… ……… 2分
= ![]() ……… … 4分
……… … 4分
= ![]() ……… …6分
……… …6分
18.(1)证明 △=![]() , ……… …2分
, ……… …2分
原方程有两个不相等的实数根 ………… 3分
(2)解:由根与系数的关系,得 ![]() .4分
.4分
![]()
![]() ……… ……… … 5分
……… ……… … 5分
解得k=1 …………· 6分
19.解:(1)过点A作AD⊥x轴,垂足为D
则OD=OA cos60°=2×![]() =1, …… 1分
=1, …… 1分
 AD=OA
sin60°=2×
AD=OA
sin60°=2×![]() =
=![]() , …… 2分
, …… 2分
∴点A的坐标为(1,![]() )
……3
)
……3
(2)设直线AB的解析式为y=kx+b,
则有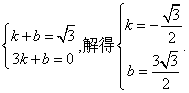 ……4分
……4分
∴直线AB的解析式为![]() y … … 5分
y … … 5分
令x=0,得![]() ,∴
,∴![]()
![]() … … 6分
… … 6分
20.(1)不同类型的正确结论不惟一.以下答案供参考:
①BE=CE ![]() ②,③∠BED=90°④∠BOD=∠A,
⑤AC∥OD
②,③∠BED=90°④∠BOD=∠A,
⑤AC∥OD
⑥AC⊥BC ⑦![]() ⑧
⑧![]() ⑨ΔBOD是等腰三角形⑩ΔBOE∽ΔBAC等,
⑨ΔBOD是等腰三角形⑩ΔBOE∽ΔBAC等,
说明:1每写对一条给1分,但最多只给3分;
2结论与辅助线有关且正确的,也相应给分
(2) ![]() 与
与![]() 的关系式主要有如下两种形式,请参照评分:
的关系式主要有如下两种形式,请参照评分:
①答;![]() 与
与![]() 之间的关系式为
之间的关系式为![]() -
-![]() =90° …… 4分
=90° …… 4分
证明:∵AB为⊙O的直径,∴∠A+∠ABC=90°
又∵四边形ACDB为圆的内接四边形,∴∠A+∠CDB=180°
∴∠CDB-∠ABC=90°
即![]() -
-![]() = 90°
……6分
= 90°
……6分
说明:关系式写成![]() = 90°+
= 90°+![]() 或
或![]() =
=![]() -90°均参照给分
-90°均参照给分
②答![]() 与
与![]() 之间的关系式为;
之间的关系式为;![]() >2
>2![]() ……4分
……4分
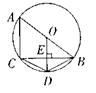 证明
∵ OD=OB
, ∴∠ODB=∠ OBD
证明
∵ OD=OB
, ∴∠ODB=∠ OBD
又∵∠ OBD=∠ABC+∠CBD ∴∠ODB>∠ABC
∵OD⊥BC
∴![]() ∴CD=BD ……5分
∴CD=BD ……5分
∴∠CDO=∠ODB=![]() ∠CDB
∠CDB
∴![]() ∠CDB>∠ABC
∠CDB>∠ABC
![]() >2
>2![]() ……6分
……6分
说明:若得 出与![]() 与
与![]() 的关系式为
的关系式为![]() >
>![]() ,且证明正确的也给满分
,且证明正确的也给满分
四、(本大题共3小题,每小题8分.共24分)
2I(1)证明根据题意可得;
 CD=
CD=![]() D,∠
D,∠![]() DE=∠CDE
……1分
DE=∠CDE
……1分
∵AD∥BC ∴∠![]() DE=∠CED ……2分
DE=∠CED ……2分
∴∠CDE=∠CED ……3分
∴CD= ![]() D =
D =![]() E=CE ……4分
E=CE ……4分
∴四边形CD![]() E是菱形
……5分
E是菱形
……5分
(2)答:当BC=CD+AD时,四边形ABED为平行四边形 ……… 6分
证明:由(1)知CE=CD
又∵BC=CD+AD ∴BE=AD ……… 7分
又∵AD∥BE ∴四边形ABED为平行四边形 ……… 8分
22.解(1)数学考试成绩的平均分![]() ……… 2分
……… 2分
英话考试成绩的标准差
![]() ……4分
……4分
(2)设A同学数学考试成绩标准分为P![]() ,英语考试成绩标准分为P
,英语考试成绩标准分为P![]() ,则
,则
P![]() =
=![]() ……5分
……5分
P![]()
![]() ……6分
……6分
P![]() > P
> P![]()
从标准分看,A同学数学比英语考得更好 ……8分
23.解(1)小杰继续在A窗口排队到达A窗口所花的时间为
![]() (分)
………3分
(分)
………3分
(2)由题意.得![]() ………6分
………6分
解得a>20
a的取值范围为a>20 ………8分
五、(本大题共2小题,每小题12分.共24分)
24.解:(1)由题意,得;![]() ………3分
………3分
抛物线的解析式为![]() …… ……4分
…… ……4分
(2)当⊙P在运动过程中,存在⊙P与坐标轴相切的情况.
设点P坐标为(![]() ),则
),则
则当⊙P与y轴相切时,有![]() =1,
=1,![]() =±1
=±1
 由
由![]() = -1,得
= -1,得![]() ,…… ……5分
,…… ……5分
由![]() = 1,得
= 1,得![]() …… ……6分
…… ……6分
当⊙P与x轴相切时有![]()
∵ 抛物线开口向上,且顶点在x轴的上方.∴![]() =1
=1
由![]() =1,得
=1,得![]() ,解得
,解得![]() =2,B(2,1)
=2,B(2,1)
综上所述,符合要求的圆心P有三个,其坐标分别为:
![]() ………… 8分
………… 8分
(3)设点Q坐标为(x,y),则当⊙Q与两条坐标轴都相切时,有y=![]() x
x
由y=x得![]() ,即
,即![]() ,解得
,解得![]() …… 10分
…… 10分
由y=-x,得![]() .即
.即![]() ,此方程无解 … I 1分
,此方程无解 … I 1分
 ∴⊙O的半径为
∴⊙O的半径为 ![]() …… …………12分
…… …………12分
25(1)根据选择命题的难易程度评分,以下答案供参考:
(1) 如选命题①
证明:在图1中,∵∠BON=60°∴∠1+∠2=60° … 1分
∵∠3+∠2=60°,∴∠1=∠3 … 2分
又∵BC=CA,∠BCM=∠CAN=60°∴ΔBCM≌ΔCAN … 3分
∴BM=CN … 4分
(2)如选命题②
证明:在图2中,∵∵∠BON=90°∴∠1+∠2=90°
∵∠3+∠2=90°,∴∠1=∠3 … 1分
又∵BC=CD,∠BCM=∠CDN=90°∴ΔBCM≌ΔCDN … 2分
∴BM=CN … 3分
(3)如选命题③
证明;在图3中,∵∠BON=108°∴∠1+∠2=108° … 1分
∵∠2+∠3=108°∴∠1=∠3 … 2分
又∵BC=CD,∠BCM=∠CDN=108°………3分
∴ΔBCM≌ΔCDN ……… 4分
∴BM=CN … 5分
(2)①答:当∠BON=![]() 时结论BM=CN成立.…2分
时结论BM=CN成立.…2分
②答当∠BON=108°时。BM=CN还成立 …1分
证明;如图5连结BD、CE.
在△BCI)和△CDE中
∵BC=CD, ∠BCD=∠CDE=108°,CD=DE
∴ΔBCD≌ ΔCDE …2分
∴BD=CE , ∠BDC=∠CED, ∠DBC=∠CEN
∵∠CDE=∠DEC=108°, ∴∠BDM=∠CEN … 3分
∵∠OBC+∠ECD=108°, ∠OCB+∠OCD=108°
∴∠MBC=∠NCD
又∵∠DBC=∠ECD=36°, ∴∠DBM=∠ECN ….4分
∴ΔBDM≌ ΔCNE ∴BM=CN …. 5分
说明:1第(1)小题第(I)问4分,第(2)问3分,第(3)问5分.
2第(2)小题第①问2分,第②问5分