中考数学专题训练 （九） 四边形
一、选择题：
1．七边形的对角线的条数是（ ）
（A）10 （B）12 （C）14 （D）16
2.下列图形中,既是中心对称图形，又是轴对称图形的是( )
(A)平行四边形
(B)等边三角形 (C)矩形 (D)等腰梯形
3．如右图，梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，
则图中面积相等三角形有（ ）
（A）1对 （B）2对 （C）3对 （D）4对
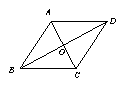4. 如图,菱形ABCD的面积为2
,∠ABC∶∠BAD=1∶2,则下列结论:
①∠ABC=600.②∠ABO=300.③ AC=2.④BD=2.⑤菱形ABCD的周长是8.
其中正确的有（ ）
（A）①②③④⑤.（B）①②③④.（C）②③④⑤.（D）①②③.
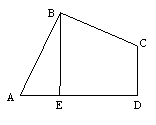
5.如图,四边形ABCD中,若AB=BC，∠ABC=∠CDA=900，BE⊥AD于点E，
=8，则BE的长为（ ）
（A）2 （B）3 （C）
（D）
6．直角梯形的一个内角为
，较长的腰为6cm，一底为5cm，则这个梯形的面积为（ ）
（A）
.（B）
.（C）25
.（D）或.
7．使用同一种规格的下列地砖，不能密铺的是 （ ）
（A）正六边形地砖 （B）正五边形地砖
（C）正方形地砖 （D）正三角形地砖
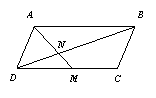
8．如图，在□ABCD中，如果点M为CD中点，AM与BD相交于点 N，
那么S△DMN∶S□ABCD为 （ ）
（A）1∶12 （B）1∶9 （C）1∶8 （D）1∶6
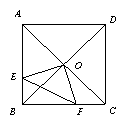
9． 如图，正方形ABCD的对角线交于O，过O点作OE⊥OF，
分别交AB BC于E，F，若AE＝4，CF＝3，则EF等于（ ）
（A）7 （B）5 （C）4 （D）3
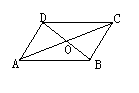10．如图，
ABCD中，对角线AC和BD相交于点O，如果AC=12、BD=10、AB=m，那么m的取什范围是( )
（A）1＜m＜11 （B）2＜m＜22
（C）10＜m＜12 （D）5＜m＜6
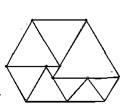
11．如下左图是由9个等边三角形拼成的六边形，现已知中间最小的等边三角形的边长是a，则围成的六边形的周长为
（A）30a （B）32a （C）34a （D）无法计算
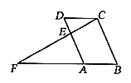
12． 如上右图，在平行四边形ABCD中，E是AD上一点，连结CE并延长交BA的延长线于F，则下列结论中错误的是（ ）
（A）∠AEF＝∠DEC （B） FA:CD＝AE:BC （ C） FA:AB＝FE:EC （D） AB＝DC
13．以线段a=16, b=13, c=10, d=6为边作梯形,其中a,c作为梯形的两底,这样的梯形( )
（A） 可以作一个 （ B）可以作二个
（C）可以作无数个 （ D） 不能作
14. 如下左图把一个正方形三次对折后沿虚线剪下，则所得图形大致是（ ）
 | |||
 | |||
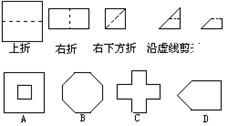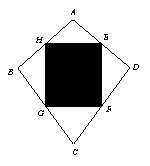
15．小明的爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如上右图所示的风筝，点E、F、G、H分别是四边形ABCD的各边中点，其中阴影部分用甲布料，其余部分用乙布料，（裁剪两种布料时，均不计余料）。若生产这批风筝需甲布料30匹，那么乙布料需（ ）
（A）15匹 （B）20匹 （C）30匹 （D）60匹
二、填空题：
1．如果一个n边形去掉一个角后的内角和等于540°，那么这个n边形的边数可能是_____.
2．如图，菱形ABCD的对角线的长分别为2和5，P是对角线
AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD
交AD于F，则阴影部分的面积是_______.
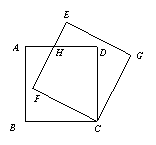
4．如图，边长为3的正方形ABCD绕点C按顺时针方向
旋转30度后得到正方形EFCG，EF交AD于点H，那么
DH长为______________。
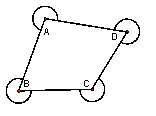3．如图，ABCD是各边长都大于2的四边形，
分别以它的顶点为圆心、1为半径画弧（弧
的端点分别在四边形的相邻两边上），则这
4条弧长的和是_______________。
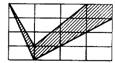
5．如图是阳光广告公司为某种商品设计的商标图案，
图中阴影部分为红色。若每个小长方形的面积都1，则红色的面
积是 。
二、解答题：
1．如图， ABCD的对角线相交于点O，且AD≠CD，过点O作OM⊥AC，交AD于点M，如果△CDM的周长是40㎝，求 ABCD的周长。（8分）
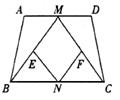
2．如图，等腰梯形ABCD中，AD∥BC，M、N分别是AD、BC的中点，E、F分别是BM、CM的中点。
⑴求证：四边形MENF是菱形；
⑵若四边形MENF是正方形，请探索等腰梯形
ABCD的高和底边BC的数量关系，并证明你的结论。
 |
3．如图是一面矩形彩旗完全展平时的尺寸图，（单位：cm），其中矩形ABCD 是由双层白布缝制的穿旗杆用的旗裤，阴影部分DCEF为矩形绸缎旗面。
（1）用经加工的圆木杆穿入旗裤作旗杆，求旗杆的最大直径（精确到1cm）；
（2）将穿好彩旗的旗杆垂直插在操场上，旗杆从旗顶到地面的高度为220cm，在无风的天气里，彩旗自然下垂（如图），求彩旗下垂时最低处离地面的高度。
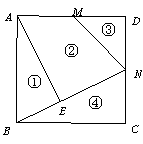
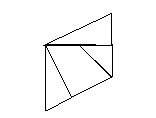
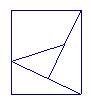
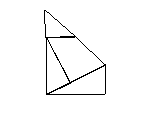
4、如图，M、N分别为正方形的边AD、DC的中点，AE ⊥BN ，把正方形如右图裁成四块，你能拼成几种其他的特殊四边形？请你画出图形。
 |
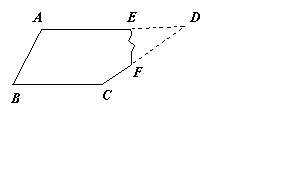
5．有一块如图的玻璃，不小心把DEF 部分打碎，现在只测得AB=60cm ，BC=80cm ，
∠A=120°， ∠B=60°， ∠C=150°，你能根据测得的数据计算AD的长吗?
 |
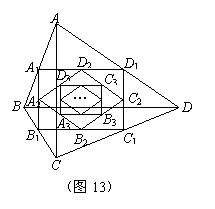
6．如图，四边形ABCD中，AC=6，BD=8且AC⊥BD顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1；再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2……如此进行下去得到四边形AnBnCnDn .
（1）证明：四边形A1B1C1D1是矩形；（6分）
（2）写出四边形A1B1C1D1和四边形A2B2C2D2的面积；（2分）
（3）写出四边形AnBnCnDn的面积；（2分）
（4）求四边形A5B5C5D5的周长.（4分）
_
答案：
一选择题：（1）C (2) C (3) C （4） A (5) D (6) D （7）B （8）A
（9）B （10）A （11）A （12 ）B （13）D （14）A （15）C
二填空题：
（1）四边形或五边形或六边形
(2) 5/2 (3) （4）3π (5)5
三解答题：
1． 80cm
2． ⑴证明：∵ABCD是等腰梯形，M是AD的中点
∴BM=CM (ABMCDM)
又∵N、E、F分别为BC，MB，CM的中点
∴四边形MENF是菱形
⑵若菱形MENF是正方形，则∠BMC=90°，
∴∠MBC=∠MCB=45°，
在Rt△MNB中，∠MBC=45°，∴MN=BN
又∵MB=NC ∴MN=
BC 即等腰梯形ABCD的高MN=BC
3．旗杆的最大直径约3 cm， 彩旗下垂时最低处离地面的高度70cm 。
4、
 | |||
 | |||
5．解：过D作AB的平行线 ，交BC的延长线于G，
则∠3＝∠1＝30°，且∠ADG =180°－∠A ＝ 60°，
又由AD∥BC ， 得 ABGD ，
∴BG=AD ， DG=AB=60cm ．∴ ∠2=60°－∠3 ＝30°．
∴ ∠2=∠1 ．∴ CG=DG=60cm ． ∴ AD=BG =BC+CG=140cm ．
6（1）证明∵点A1，D1分别是AB、AD的中点，∴A1D1是△ABD的中位线
∴A1D1∥BD，
，同理：B1C1∥BD ，
∴
∥
，=， ∴四边形
是平行四边形
∵AC⊥BD，AC∥A1B1，BD∥，∴A1B1⊥ 即∠B1A1D1=90°
∴四边形是矩形
（2）四边形的面积为12；四边形
的面积为6；
（3）四边形
的面积为
；
（4）方法一：由（1）得矩形的长为4，宽为3；
∵矩形
∽矩形；∴可设矩形的长为4x,宽为3x，则
解得
；∴
；
∴矩形的周长=
.
方法二：矩形的面积/矩形的面积
=（矩形的周长）2/（矩形的周长）2
即
∶12 =（矩形的周长）2∶142
∴矩形的周长=