内蒙古包头市高中招生考试数学试卷及答案

2005年内蒙古包头市高中招生考试数学试卷

(满分120分，考试时间120分钟)

参考公式：S²=[(x₁―)²+(x₂―)²+…+(x_n―)²]　　　 S²=(x₁²+x₂²+……+x_n²)―²

　　　　 多边形内角和=(n—2)×180º

一、选择题：(本大题共有12小题，每小题3分，共36分。每小题只有一个正确选项)

1．5的倒数是(　　)

  A．—5　　　　　　　  B．　　　　　　　 C．—　　　　　　　　　 D．5

2．函数y=中，自变量x的取值范围是( 　 )

  A．x≥2　　　　　　　 B．x＞2　　　　　　  C．x≠2　　　　　　　 D．x≤2

3．将不等式组的解集表示在数轴上，正确的是(　 )

4．已知点A(1，5)在反比例函数y=的图像上，则该反比例函数的解析式是(　　)

  A．y=　　　　　　　 B．y=　　　　　　 C．y=　　　　　  D．y=5x

5．已知在Rt△ABC中，∠C=90º，cosA=，则sinB的值是(　 )

A．　　　　　　　  B．　　　　　　  C．　　　　　　  D．

6．据测算，我国每天因土地沙漠化造成的经济损失为元，这个数用科学记数法表示为(　　　 )

  A．15×10⁷　　　　　 B．1.5×10⁸　　　　　 C．15×10⁸　　　　 D．0.15×10⁹

7．下列图形中对称轴最多的图形是(　　  )

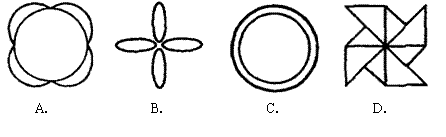
8．小明家准备选用两种形状的地板砖铺地，现在家中已有正六边形地板砖，下列形状的地板砖能与正六边形的地板砖共同使用的是(　　)

　A．正三角形　　　　　  B．正四边形　　　　  C．正五边形　　　D．正八边形

9．已知二次函数y=x²+bx+3，当x=—1时，y取得最小值，则这个二次函数图像的顶点在(　)

A．第一象限　 　　　 B．第二象限　　　　　C．第三象限　　　　D．第四象限

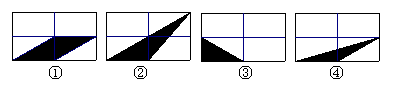10．如图将四个全等的矩形分别等分成四个全等的小矩形，其中阴影部分面积相等的是(　)

A．只有①和②相等　　　　　　　 B．只有③和④相等　

C．只有①和④相等　　　　　　　 D．①和②，③和④分别相等

11．已知下列命题：①半圆是弧；②若am²＞bm²，则a＞b；③若x²=y²，则x=y；④垂直于弦的直径平分这条弦。其中原命题与逆命题均为真命题的个数是(　 )

  A．1个　　　　　　　 B．2个　　　　　　 C．3个　　　　　　　 D．4个

甲	8	5	7	8	7
乙	7	8	6	8	6

12．甲、乙两名同学在相同条件下各射击5次，命中的环数如下表：那么下列结论正确的是(　)

  A．甲的平均数是7，方差是1.2　　　　　 C．甲的平均数是8，方差是1.2

  B．乙的平均数是7，方差是1.2　　　　　 D．乙的平均数是8，方差是0.8

二、填空题：(本大题共有8小题，每小题3分，共24分)

13．坐标平面内点P(m，2)与点Q(3，—2)关于原点对称，则m=_____。

14．把多项式xy―x+y―1分解因式，其结果是__________________。

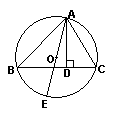
15．如图，AD是△ABC的高，AE是△ABC的外接圆⊙O的直径，且

AC=5，DC=3，AB=4，则⊙O的直径AE=_____。

16．若一次函数y=ax+1―a中，y随x的增大而增大，且它的

图像与y轴交于正半轴，则a―1+=_____。

17．解方程+=7时，利用换元法将原方程化为

6y²—7y+2=0，则应设y=_____。

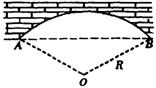
18．如图，有一圆弧形桥拱，拱的跨度AB=30m，拱形的

半径R=30m，则拱形的弧长等于_____m。

19．如图，在Rt△ABC中，∠ACB=90º，∠A＜∠B，以AB边上的

中线CM为折痕将△ACM折叠，使点A落在点D处。如果CD

恰好与AB垂直，则tanA=_____。

20．随着通讯市场竞争日益激烈，为了占领市场，甲公司推出的优惠措施是：每分钟降低a元后，再下调25％；乙公司推出的优惠措施是：每分钟下调25％，再降低a元。若甲、乙两公司原来每分钟收费标准相同，则收费较便宜的是_____公司。

三、解答题：本大题共有6小题，共60分。解答时要求写出必要的文字说明、计算过程或推理过程。

21．(本小题满分8分)

  已知关于x的一元二次方程2x²+4x+m=0。

(1)若x=1是方程的一个根，求方程的另一个根；(4分)

(2)若x₁、x₂是方程的两个不同的实数根，且x₁和x₂满足：x₁²+x₂²+2x₁x₂―x₁²x₂²=0，求m的值。(4分)

22．(本小题满分8分)

  如图，甲楼在乙楼的南面，它们的设计高度是若干层，每层高均为3米，冬天太阳光与水平面的夹角为30º。

  (1)若要求甲楼和乙楼的设计高度均为6层，且冬天甲楼的影子不能落在乙楼上，那么建筑时两搂之间的距离BD至少为多少米?(保留根号)(4分)

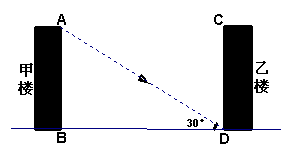　(2)由于受空间的限制，甲楼和乙楼的距离BD=21米，若仍要求冬天甲楼的影子不能落在乙楼上，那么设计甲楼时，最高应建几层?(4分)

23．(本小题满分9分)

  学校鼓励学生参加社会实践，小明和他的同学利用寒假一周时间对市公交10路车起点站的一周乘车人次进行了统计，以每天800人次为准，超过的人次记为正数，不足的人次记为负数。记录一周情况如下：

星期一	星期二	星期三	星期四	星期五	星期六	星期日
50	400	―50	300	―100	377	430

(1)求该起点站在这一周内平均每天乘客的人次，并估计一下2005年6月份(30天)该起点站乘客的总人次；(4分)

(2)若将2005年6月份该起点站每天乘客人次整理后，按人次由小到大排列，分成五组，且每组的频率之比依次为1∶2∶1∶3∶3，请你说明这个月该起点站乘客人次的中位数能否落在某个小组内。(5分)

24．(本小题满分10分)

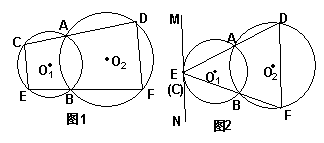
  如图1，⊙O₁与⊙O₂都经过A、B两点，经过点A的直线CD与⊙O₁交于点C，与⊙O₂交于点D。经过点B的直线EF与⊙O₁交于点E，与⊙O₂交于点F。

  (1)求证：CE∥DF；(4分)

  (2)在图1中，若CD和EF可以分别绕点A和点B转动，当点C与点E重合时(如图2)，过点E作直线MN∥DF，试判断直线MN与⊙O₁的位置关系，并证明你的结论。(6分)

25．(本小题满分12分)

  小明计划将今年春节期间得到的压岁钱的一部分作为自己一年内购买课外书籍的费用，其余的钱计划买些玩具去看望市福利院的孩子们。某周日小明在商店选中了一种小熊玩具，单价是10元，按原计划买了若干个，结果他的压岁钱还余30％，于是小明又多买了6个小熊玩具，这样余下的钱仅是压岁钱的10％。

  (1)问小明原计划买几个小熊玩具，小明的压岁钱共有多少元；(6分)

  (2)为了保证小明购书费用不少于压岁钱的20％，问小明最多可比原计划多买几个小熊玩具。(6分)

26．(本小题满分13分)

  已知一次函数y₁=x，二次函数y₂=x²+。

  (1)根据表中给出的x的值，填写表中空白处的值；(2分)

x	―3	―2	―1	0	1	2	3
y1=x	―3	―2	―1	0	1	2	3
y2=x2+			1		1

  (2)观察上述表格中的数据，对于x的同一个值，判断y_l和y₂的大小关系。并证明：在实数范围内，对于x的同一个值，这两个函数所对应的函数值y₁和y₂的大小关系仍然成立；(6分)

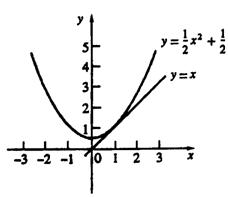　(3)若把y₁=x换成与它平行的直线y=x+k(k为任意非零实数)，请进一步探究：当k满足什么条件时，(2)中的结论仍然成立；当k满足什么条件时，(2)中的结论不能对任意的实数x都成立，并确定使(2)中的结论不成立的x的范围。

  (5分)

2005年内蒙古包头市高中招生考试数学试卷答案