第十讲 图形变换和相似图形
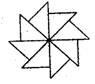
1、（2005年苏州）右图可以看作是一个等腰直角三角形旋转若干次而生成的则每
次旋转的度数可以是（ ）
A．900 B．600 C．450 D．300
2、（2004年海淀）下列交通标志图中，属于轴对称图形的是（ ）
3、（2004年湖北彬州）下列图案中不是中心对称图形的是（ ）
 | |||||||
 | |||||||
 |  | ||||||
A B C D
4、（2004年湖北黄石）下列图案中，即是轴对称图形又是中心对称图形的是（ ）
 |
5、（2004江苏南通）下列图形中既是轴对称图形又是中心对称图形的是（ ）
A B C D
6、（2004年江苏无锡）下面给出的是一些产品的商标图案，从几何图形的角度看(不考虑文字和字母)，这些图案中的中心对称图形是（ ）
 |
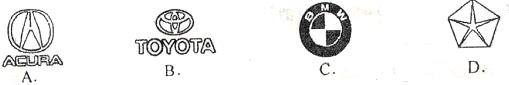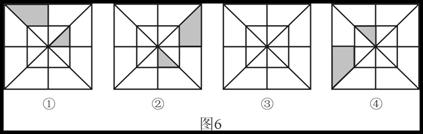
7、（2004•四川资阳）分析图6①,②,④中阴影部分的分布规律，按此规律在图6③中画出其中的阴影部分.
8、（2005年湖北宜昌）某城市进行旧城区人行道的路面翻新,准备对地面密铺彩色地砖, 有人提出了4种地砖的形状供设计选用：①正三角形，②正四边形，③正五边形，④正六边形．其中不能进行密铺的地砖的形状是（ ）.
A、 ① B、② C、③ D、④
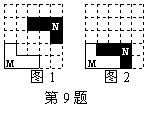
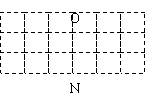
9、（2005年湖北宜昌）在5×5方格纸中将图（1）中的图形N平移后的位置如图（2）中所示，那么正确的平移方法是（ ）.
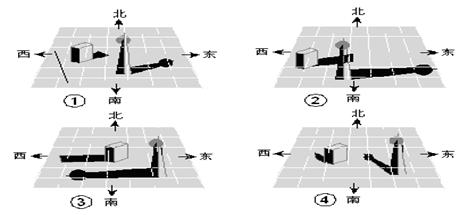
A、先向下移动1格，再向左移动1格 B、先向下移动1格，再向左移动2格
C、先向下移动2格，再向左移动1格 D、先向下移动2格，再向左移动2格
10、（2004年绍兴）4张扑克牌如图（1）所示放在桌子上，小敏把其中一张旋转180º后得到如图（2）所示，那么她所旋转的牌从左数起是（ ）
A、第一张 B、第二张 C、第三张 D、第四张
11、（2004年山东日照）在日常生活中，你会注意到有一些含有特殊数学规律的车牌号码，，如：鲁L80808 、鲁L22222、鲁L12321等，这些牌照中的五个数字都是关于中间的一个数字“对称”的，给以对称的美的感受，我们不妨把这样的牌照叫做“数字对称”牌照。如果让你负责制作只以8和9开头且有五个数字的“数字对称”牌照，那么最多可制作（ ）
A、2000个 B、1000个 C、200个 D、100个
12、（2004年衢州）下列几个图形是国际通用的交通标志，其中不是中心对称图形的是（ ）
 |  | ||||||
 | |||||||
 | |||||||
A B C D
15、（2005年湖北恩施）下面给出的是一些产品的图案，从几何图形的角度看，这些图案既是中心对称图形又是轴对称图形的是（ ）
A.
B．
C．
D．
16、（2005年深圳）图所列图形中是中心对称图形的为（ ）
A B C D
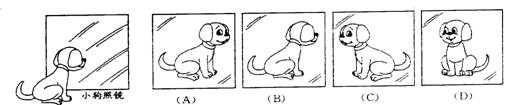17、（2005年台州）一只小狗正在平面镜前欣赏自己的全身像（如图所示），此时，它所看到的全身像是(
)
18、（2005年温州）下列图形中，既是轴对称图形又是中心对称图形的是( )
19、（2005年四川）下面有4个汽车标致图案，其中是轴对称图形的是（ ）
① ② ③ ④
A、②③④ B、①③④ C、①②④ D、①②③
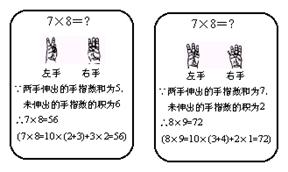
20、（2005年河北实验区） 法国的“小九九”从“一一得一”
到“五五二十五”和我国的“小九九”是一样的，后面的就改用手
势了。右面两个图框是用法国“小九九”计算78和89的两个示例。
若用法国“小九九”计算79，左右手依次伸出手指的个数是( )
A、2，3 B、3，3 C、2，4 D、3，4
21、（2005年常州）下面是一天中四个不同时刻两个建筑物的影子：将它们按时间先后顺序进行排列，正确的是
A、③④②① B、②④③① C、③④①② D、③①②④
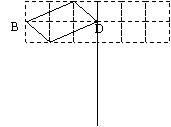
22、（2005年宁波）已知：如图， ABCD.
(1)画出 A1B1C1D1使 A1B1C1D1与 ABCD关于直线MN对称;
(2)画出 A2B2C2D2,使 A2B2C2D2与 ◇ABCD关于点O中心对称;
|
|
(3) A1B1C1D1与 A2B2C2D2是对称图形吗?若是,请在图上画出对称轴或对称中心
 | |||
 | |||
|
 |
第23题 第22题
23、（2005年南京）如图，身高为1.6m的某学生想测量一棵大树的高度，她沿着树影BA由B到A走去，当走到
C点时，她的影子顶端正好与树的影子顶端重合，测得BC=3.2m ,CA=0.8m, 则树的高度为（ ）
A、4.8m B、6.4m C、8m D、10m
24、（2005年大连实验区）下列图形中只能用其中一部分平移可以得到的是 （
）
 | |||||
 | |||||
 | |||||
A
B
C
D
25、（2005年陕西）如图，在一个由4×4个小正方形组成的正方形网格中，
阴影部分面积与正方形ABCD的面积比是 （ B ）
A.3：4 B.5：8 C.9：16 D.1：2
26、（2004年哈尔滨）若
，则
=
。
27、（2004年杭州）右图为羽毛球单打场地按比例缩小的示意图
（由图中粗实线表示），它的宽度为5.18米，那么它的长大约
在（ ）
（A）12米至13米之间 （B）13米至14米之间
（C）14米至15米之间 （D）15米至16米之间
28、（2004年资阳实验区）如图2，若A、B、C、P、Q、甲、乙、丙、丁
都是方格纸中的格点，为使△ABC∽△PQR，则点R应是甲、乙、
丙、丁四点中的（ ）
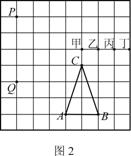A、甲 B、乙
C、丙 D、丁
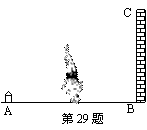
第28题 第30题
29、（2005年佛山实验区）如图：地面A处有一支燃烧的蜡烛(长度不计)，一个人在A与墙BC之间运动，则他在墙上的投影长度随着他离墙的距离变小而 (填“变大”、“变小”或“不变”).
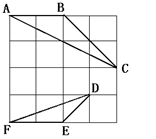
30、（2005年台州）如图，在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上。
（1）填空：∠ABC= °，BC= ；
（2）判断△ABC与△DEF是否相似，并证明你的结论。
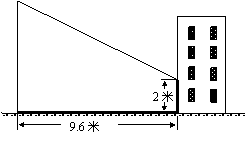
31、（2005年荆州）赵亮同学想利用影长测量学校旗杆的高度，如图，他在某一时刻立1米长的标杆测得其影长为1.2米，同时旗杆的投影一部分在地面上，另一部分在某一建筑的墙上，分别测得其长度为9.6米和2米，则学校旗杆的高度为 米．
32、（2005年安徽）图(1)是一个10×10格点正方形组成的网格. △ABC是格点三角形(顶点在网格交点处), 请你完成下面两个问题：
(1) 在图(1)中画出与△ABC相似的格点△A1B1C1和△A2B2C2, 且△A1B1C1与△ABC的相似比是2, △A2B2C2与△ABC的相似比是
；
(2) 在图(2)中用与△ABC、△A1B1C1、△A2B2C2全等的格点三角形(每个三角形至少使用一次), 拼出一个你熟悉的图案,并为你设计的图案配一句贴切的解说词。
33、（2005年天津）在△ABC中，∠A、∠B、∠C所对的边分别用a、b、c表示。
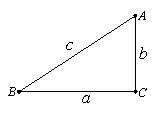（Ⅰ）如图，在△ABC中，∠A＝2∠B，且∠A＝60°。求证：a2＝b（b＋c）
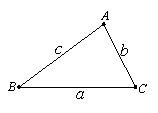（Ⅱ）如果一个三角形的一个内角等于另一个内角的2 倍，我们称这样的三角形为“倍角三角形”。本题第一问中的三角形是一个特殊的倍角三角形，那么对于任意的倍角三角形ABC，其中∠A＝2∠B，关系式a2＝b（b＋c）是否仍然成了？并证明你的结论；
（Ⅲ）试求出一个倍角三角形的三条边的长，使这三条边长恰为三个连续的正整数。
34、（2005年无锡）如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点（P异于A、D），Q是BC边上的任意一点. 连AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F.
（1）求证：△APE∽△ADQ；
（2）设AP的长为x，试求△PEF的面积S△PEF关于x的函数关系式，并求当P在何处时，S△PEF取得最大值？最大值为多少？
（3）当Q在何处时，△ADQ的周长最小？（须给出确定Q在何处的过程或方法，不必给出证明）
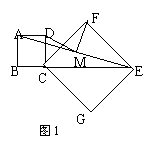35、（2005年大连）如图13－1，操作：把正方形CGEF的对角线
CE放在正方形ABCD的边BC的延长线上（CG＞BC），
取线段AE的中点M。
探究：线段MD、MF的关系，并加以证明。
说明：（1）如果你经历反复探索，没有找到解决问题
的方法，请你把探索过程中的某种思路写出来（要求
至少写3步）；（2）在你经历说明（1）的过程之后，
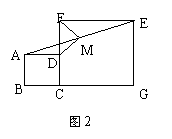可以从下列①、②、③中选取一个补充或更换已知条件，
完成你的证明。
注意：选取①完成证明得10分；选取②完成证明得
7分；选取③完成证明得5分。
① DM的延长线交CE于点N，且AD＝NE；
② 将正方形CGEF绕点C逆时针旋转45°（如图13－2），
其他条件不变；③在②的条件下且CF＝2AD。
附加题：将正方形CGEF绕点C旋转任意角度后
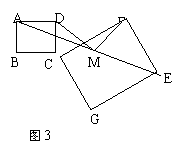（如图13－3），其他条件不变。探究：线段MD、
MF的关系，并加以证明。
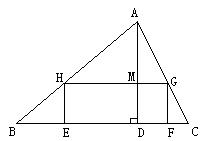
36、（2005年四省实验区）如图，要在底边BC＝160cm，高AD＝120cm，的△ABC铁皮余料上截取一个矩形EFGH，使点H在AB上，点G在AC上，点E、F在BC上，AD交HG于点M，此时
.
（1）设矩形EFGH的长HG＝y，宽HE＝x，确定y与x的函数关系式；
（2）当x为何值时，矩形EFGH的面积S最大；
（3）以面积最大的矩形EFGH为侧面，围成一个圆柱形的铁桶，怎样围时，才能使铁桶的体积最大？请说明理由（注：围铁桶侧面时，接缝无重叠，底面另用材料配备）.
