第二章 方程和不等式测试题
龙丰学校
一、填空题 选择题
1、（04年海口市4）把分式方程
的两边同时乘以（x-2），约去分母，得（ ）
A、1-（1-x）=1 B、1+（1-x）=1
C、1-（1-x）= x-2 D、1+（1-x）= x-2
2、（青岛04 2）用换元法解方程
时，若设
，则原方程可化为（ ）.
3、（大连 04 4）一元二次方程
的根的情况是( )
A、有一个实数根 B、有两个相等的实数根
C、有两个不相等的实数根 D、没有实数根
4、（05年扬州市10）关于x的方程
有实数根，则k的取值范围是（ ）．
A．
B．
C．
D．
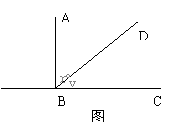5、(04年南山5)如图3，AB⊥BC，∠ABD的度数比∠DBC的度数的两倍少15°，设∠ABD和∠DBC的度数分别为x、y，那么下面可以求出这两个角的度数的方程组是
A．
B．
C．
D．
6、（05安徽7）方程x(x+3)=x+3的解是 ( )
A. x=1 B. x1=0, x2=-3 C. x1=1, x2=3 D. x1=1, x2=-3
7、（05佛山6）方程
的解是（ ）。
A．1 B．－1 C．±1 D．0
8（05年扬州市12）若方程
有增根，则它的增根是（ ）．
A．0 B．1 C．－1 D．1和－1
9、(04无锡市18)设“○”、“□”、“△”分别表示三种不同的物体，用天平比较它们质量的大小，两次情况如图所示，那么每个“○”、“□”、“△”这样的物体，按质量从小到大的顺序排列为（
）
A、○□△ B、○△□ C、□○△ D、△□○
10、（04重庆市北碚区7）关于x的不等式2x-a≤-1的解集如图所示，则a的取值是（ ）
A 、0 B 、-3 C、 -2 D、 -1
（A） （B） （C） （D）
11、(05年黑龙江省19) 不等式组
的解集是 ( )
A. x≤3 B. 1<x≤3
C. x≥3 D. x>1
12、(05年宁夏回族自治区4)把不等式组 
的解集表示在数轴上，正确的是
( )
A. B. C. D.
二、填空题
13、(大连 04 12）大连市内与庄河两地之间的距离是160千米，若汽车以平均每小时80千米的速度从大连市内开往庄河，则汽车距庄河的路程y(千米)与行驶的时间x(小时)之间的函数关系式为_______________________________________；
14、（04年青海省14）一商店把某种品牌的羊毛衫按标价的八折出售，仍可获利20%，若该品牌的羊毛衫的进价每价是100元，则标价是每件___________元.
15、(04无锡市4)设x1、x2是方程
的两实数根，则x1+x2= ，
x1·x2= .
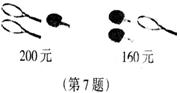
16、（05年南宁市7）根据图2提供的信息，求出每支网球拍的单价为 元，每支乒乓球拍的单价为 元。
17、(05辽宁省沈阳市12)一元二次方程
的根是 。
18、（04年山东潍坊市15）一次普法知识竞赛共有30道题,规定答对一道题得4分,答错或不答一道题得-1分,在这次竞赛中,小明获得优秀(90分或90分以上),则小明至少答对了__________道题.
19、（04年芜湖市5） 不等式组
的解集为________.
20、（05年陕西省11）不等式2(x+1)>1-x的解集为__________.
三、解答题
21、(05年武汉17)解方程：
22、(04年南山)解方程： 
23、已知方程
的一个根是-5，求它的另一个根及
的值.
24、（04年山东潍坊市21）甲、乙两件服装的成本共500元，商店老板为获取利润，决定将甲服装按50﹪的利润定价，乙服装按40﹪的利润定价。在实际出售时，应顾客要求，两件服装均按9折出售，这样商店共获利157元，求甲、乙两件服装的成本各是多少元？
25、（05年深圳市20）某项工程，甲工程队单独完成任务需要40天．若乙队先做30天后，甲、乙两队一起合做20天就恰好完成任务．请问：
（1）乙队单独做需要多少天才能完成任务？
（2）现将该工程分成两部分，甲队做其中一部分工程用了x天，乙队做另一部分工程用了y天．若x、y都是正整数，且甲队做的时间不到15天，乙队做的时间不到70天，那么两队实际各做了多少天？
26、（05福州20）请你替小健同学解答以下问题：
27、（05年河南省22）某公司为了扩大经营，决定购进6台机器用于生产某种活塞。现有甲、乙两种机器供选择，其中每种机器的价格和每台机器日生产活塞的数量如下表所示。经过预算，本次购买机器所耗资金不能超过34万元。
| 甲 | 乙 | |
| 价格（万元/台） | 7 | 5 |
| 每台日产量（个） | 100 | 60 |
（1）按该公司要求可以有几种购买方案？
（2）若该公司购进的6台机器的日生产能力不能低于380个，那么为了节约资金应选择哪种方案？