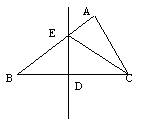初中数学“能力提高”培训题（1）
一、填空题、选择题：
1、单项式-
的系数是
；60021/的角的补角等于
．
2、把多项式
按字母x降幂排列是
．
3、轮船航行到C处测得小岛A的方向为北偏西270，那么此时从A观测C处的方向为 ．
4、有理数a、b在数轴上的位置如图所示，则a+b 0（填“＞”或“＜”或“＝”号）．
|
画3个圆点，涂上白色或红色，然后在这三个圆点处把
绳子剪断，这样所得到的各小段两端都有颜色．则两端颜色不同的小段数目一定是 （答奇数或偶数） ．
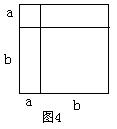
6、试用代数式表示图4中由几个小正方形和长方形并成的大正方形的面积（至少3种） ．
7、在如图所示的2×2方格图案中有多少正方形.
答: .
在3×3方格图案中有多少正方形.
答: .
在4×4和5×5方格图案中有多少正方形.
答: . .
在上面算法过程中你能否探索出用一般规律表示在n×n个
方格图案中的正方形个数表示为 .
8、学校气象小组测得一周的温度并登记在下表:
| 星期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 | 周平均气温 |
| 气温 | 22℃ | 22℃ | 24℃ | 25℃ | 23℃ | ?℃ | 26℃ | 24℃ |
记录表中,星期五的气温是( )
9、据测算．我国每天国土地沙漠化造成的经济损失为1.5亿元，若一年按365天
计算，用科学计数法表示我国一年因土地沙漠化造成的经济损失为（ ）
A．5.475×
B．5.475×
(元) C．0.5475×
(元) D．
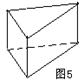
10、如图5所示的三棱柱的三视图是( )
A．三个三角形 B、三个长方形 C．两个长方形和一个三角形
D．两个长方形，且长方形内有一条连结对边的点的线段，和一个三角形
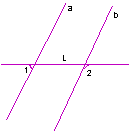
11、在图7中，∠1与∠2是同位角的有（ ）
A．①、② B．①、③ C．②、③ D．②、④
二、先化简，后求值：
，其中
．
三、探索题：
1、看一看，下列两组算式：(3×5)2与32×52 ；[
]2与
.每组两算式的计算结果是否相等？想一想，当n为正整数时，(ab)n等于什么？
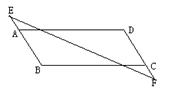
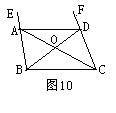
2、观察图形10，回答问题：若使AD∥BC ，需添加什么条件？
（要求：至少找出４个条件）
答：① ②
③ ④ ．
四、解答题：
社会的信息化程度越来越高，计算机、网络已进入普通百姓冢。某市电信局对计算机上网用户提供三种付费方式供用户选择、(每个用户只能选择其中一种付费方式)：
(A)计时制：3元/时．另加付通信费1.2元/时；
(B)包月制：60元/月(限一部个人住宅电话上网)，另加付通信费1.2元/时；
(C)宽带网：78元/月，不必另付通信费．
(1) 某用户某月上网的时间为ｘ小时，请你分别写出(A)、(B)两种收费方式下该用户应该支付的费用：
（2）某用户为选择适合的付费方式，连续记录了7天中每天上网所花的时间．
根据上述情况：①请你估计该用户每天上网约为多少时间? ②该用户选择哪种付费方式比较合适，请你帮助选择，并说明理由(每个月以30天计)．(单位：分)
| 日期 | 第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 |
| 上网时间 | 58 | 43 | 52 | 50 | 57 | 48 | 42 |
初中数学“能力提高”培训题（2） 姓名
一、
填空题、选择题：
1、.不在同一直线上的四点最多能确定 条直线。
2、如右图,点C是 
的边OA上一点，D、E是OB上两点，
则图中共有 条线段， 条射线, 个小于平角的角.
3、（1）
= 
（2）
4.如图,①如果
,那么根据
,
可得 // ;
如果
,那么根据
,
可得 // .
②当 // 时,根据 ,
得
;
当 // 时,
根据
,得
.
5、如图,
, 则图中与
相等的角共有( )个
A 6个 B .5个 C .4个 D.2个
6、如图，
,
,点B、O、D在同一直线上，
则
的度数为（ ）
A．
B．
C．
D．
二、解答题：
1、(1) 一个角的余角比它的补角
还多
，求这个角.
(2)已知互余两角的差为
,求这两个角的度数.
 |
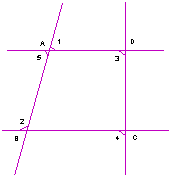
2、如图,直线
,
,
,求
的度数.
3、在下图中,已知直线AB和直线CD被直线GH所截,交点分别为E、F点，
.
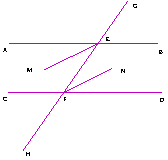（1）写出
的根据;
（2）若ME是
的平分线, FN是
的平分线,
则EM与FN平行吗?若平行,试写出根据.
 |
4、如图,已知:
,且
于D,试说明:
①
②
5、.如图， 
于D， 
于F，
，试说明DE∥BC
|
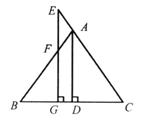
6、如图， 已知△ABC，E在CA延长线上，EG⊥BC于G，AD⊥BC于D，
若AD平分∠BAC，∠BFG=36°，求∠FEA的度数。
|
初中数学“能力提高”培训题（3）
填空题、选择题
1、若2x m －2 n y 3与－xy n是同类项，则m =
，n = 。
2、三角形有两边的长为2cm和6cm，第三边的长为xcm，则x的范围是
3、若一组数据6，7，5，6，x，1的平均数是5，则这组数的众数是
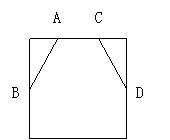
4、工人师傅在做完门框后．为防止变形常常像右图中所示的那样
钉上两条斜拉的木条（即图中的AB，CD两根木条），这样做根据
的数学道理是___ __.
5、若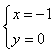
和是
方程mx
+ ny = 0的两个解，则m + n =_____．
6、已知(x + y + 1)2与2 y－x + 5互为相反数，则x 3 + y 3 + 1= 。
7、如图是“赵家镇超市”中某洗发水的价格标签，那么这种
洗发水的原价是
8、已知多边形的内角和的度数为
则这个多边形的边数为 。
9．等腰三角形两边长分别是4和5，则它的周长是 。
10、若干名学生影留念，需交照像费8元，如果另外加洗一张像片，
又需收费1.6元，结果每人平均出钱刚好2元，并都分到一张照片，
则参加照像的有 名学生。
11、若一个多边形内角和是它的外角和的5倍，则这个多边形边数是
12、若方程
和方程
有相同的解，那么a= ,b=
13、某市为了进一步缓解交通拥堵现象，决定修建一条从市中心到飞机场的轻轨铁路。为了使工程能提前3个月完成，须把原定工效提高12%。问原计划完成这一工程用 个月。
14、下列正多边形中，不能够铺满地面的是（ ）
A、正方形 B、正五边形 C、正六边形 D、正三角形
|
A、 11 B、12 C、13 D 、14
|
则下列结论可能错误的是( )
A、PC = PD B、OC = OD C、∠CPO = ∠DPO D、OC = PC
17、若五边形ABCDE中，∠A＝∠B＝∠C，∠D的外角为78°，∠D的外角与∠E互余，
则∠B的度数是( )
A、142° B、140° C、130° D、150°
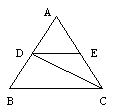
18、如图:等边三角形ABC中,CD是∠ACB的平分线,过D作BC的
平行线交AC于E,若△ADE的周长为6,则△ABC的周长是( )
A、20 B、18 C、12 D、9
二、解下列方程或方程组
1、
2、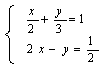 
3、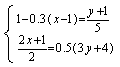
三、
|
四、某养鱼户搞池塘养鱼已两年，头年放养鲢鱼苗2万尾，成活率为70﹪，秋季打捞时随意捞取10尾，称得每尾质量分别为（单位：千克）0.8，0.9，1.2，1.3，0.8，0.9，1.1，1.0，1.2，0.8。
（1）根据样本平均数估计这塘鱼产量是多少千克？
（2）把鱼全部卖掉，市场价4元/千克，能收入多少元？除去当年投资16000元，第一年纯收入多少元？
（3）已知养鱼户这两年纯收入84000元，求第二年收入增长率是多少？
初中数学“能力提高”培训题（4） 姓名
一、填空题：
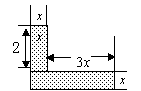
1．试以
的多项式表示右图中的面积为_____________。
2．若
，则m=_____ n=______。
3．若
是一个完全平方式，则m=____________。
4．十位数字是m，个位数字是比m小2，百位数字是m的一半，则这个三位数是___________________________。
5．如图，一等宽纸条，按图折叠后，∠1＝30°º，则∠2＝________。
 | |||
| |||
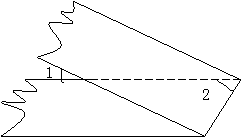(第5题) (第6题)
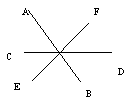
6.如图，三条直线AB、CD、EF交于同一点，若∠AOE=2∠AOC，∠COF比∠AOE大30º，则AOC的度数是_______。
7．一商品每件进价为100元，标价为120元，适应市场行情打9折销售，则该商品的总利润y(元)与售出件数x的关系是__________。
8．已知
，则
＝________。
二、选择题(4’×12)
1．若
，则M＝ (
)
A．
B.
C．
D. 
2．若m，n为自然数，则多项式
的次数应该是( )
A．m B.m+n C. n D.m，n中较大的数
3、
＝ ( )
A．1.5 B. －1.5 C. 1 D.-1
4．一个人从点A出发，沿北偏东70°方向走到点B，另一个人也从A出发，沿南偏东60°º方向走到C点，那么∠BAC的度数是 ( )
A．110º B.50º C.120º D.130º
5．三角形内一点到各边的距离相等，那么这个点一定是 ( )
A．三条中线的交点 B.三条角平分线的交点
C．三条高线的交点 D。三条垂直平分线的交点
6．AD为三角形ABC的角平分线，则
( )
A．
B.
C.
D.
7．当正方形的边长x增加了2时，则面积增加了y，则y与x的关系式为 ( )
A．
B.
C．
D.
三、解答题
1、中国民航规定：乘座飞机普通舱旅客一人最多可免费携带20千克行李，超过部分每千克按飞机票价的1.5%购买行李票。一名旅客带了35千克行李乘机，机票连同行李共付1323元，求该旅客的机票价？
2、某人装修房屋，原预算25000元。装修时因材料费下降了20％，工资涨了10％，实际用去21500元。求原来材料费及工资各是多少元？
|
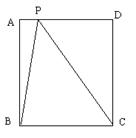
(1) 请说明图中三个三角形的面积变化情况？
(2) 如果用s表示ΔABP的面积，PD=x,则s与x的关系式什么？
(2) 当x等于多少时，ΔABP的面积是正方形面积的一半？
(3) 当x等于多少时，ΔABP的面积是正方形面积的四分之一？
初中数学“能力提高”培训题（5）（相似形） 姓名
一、填空题、选择题：
1、在比例尺为1︰500000的地图上，量得甲、乙两地的距离是25㎝，则两地的实际距离是 。
2、已知
，且3y＝2z＋6，则x＝ 、y＝ 。
3、已知：数3、6，请再写出一个数，使这个数是另外两个数的比例中项，这个数是 。
4、如图，在△ABC中，AD⊥BC，BE⊥AC，则图中有 对相似三角形，
当△ ∽△ 时，则有
；
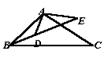
5、如图，点D是△ABC内一点，连结BD并延长到E，连结AD、AE，若∠BAD＝200，
，则∠EAC＝
|
|
6、如果两个相似三角形的面积比为8，周长比为k，那么
＝ 。
7、在△ABC中，DE∥BC，
，且S△ABC＝8cm2，那么S△ADE
8、下列说法不正确的是（ ）
A、所有等边三角形都相似 B、有一个角为120°的两个等腰三角形相似
C、所有等腰三角形都相似 D、所有的正方形都相似
二、解答题：
1、如图，DE∥BC，EF∥AB，①则图中相似形三角形有 对，分别是 。
②如果AD＝5，DB＝3，FC＝2，则△ADE与△ABC的相似比是 ； 
如何求出BF的长？
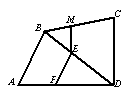2、如图，在四边形ABCD中，E是对角线BD上的一点，EF∥AB，EM∥CD， 求
的值。
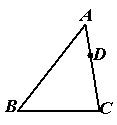3、如图，在△ABC中，AB＝8，AC＝6，点D在AC上，AD＝2，试在AB上求一点E，
使△ADE和△ABC相似，并求出AE的长。
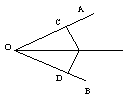
4、如图，点C、D在线段AB上，△PCD是等边三角形，①当AC、CD、BD满足怎样的关系时，△ACP∽△PDB？②当△ACP∽△PDB时，求∠APB的度数。
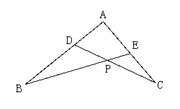5、已知：ΔABE中，D在AB上，C在AE延长线上，CD与BE相交于P，AD·AB=AE·AC
试说明：ΔPBD∽ΔPCE
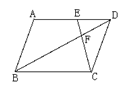6、已知：如图， ABCD中，E是AD上一点
， CE交BD于点F，BF=21cm求：DF的长
7、在△ABC中，∠C＝900，BC＝8㎝，AC︰AC＝3︰5，点P从点B出发，沿BC向点C以2㎝/s的速度移动，点Q从点C出发沿CA向点A以1㎝/s的速度移动，如果P、Q分别从B、C同时出发：
⑴经过多少秒△CPQ∽△CBA？
⑵经过多少秒时，以C、P、Q为顶点的三角形恰与△ABC相似