高中提前考数学模拟检测试题
一、选择题（每小题5分，共40分）
1. 如图是一个经过改造的台球桌面示意图，图中四个角上的阴影部分分别表示四个入球孔。如果一个球按图中所示的方向被击出（球可以经过多次反射），那么该球最后将落入---（ ）
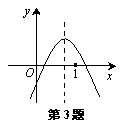A．一号袋
B．二号袋 C．三号袋 D．四号袋
 | |||
 | |||
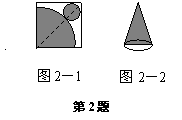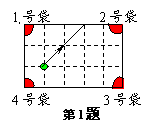
2. 如图2—1，在正方形铁皮上剪下一个圆形和扇形，使之恰好围城图2—2所示的一个圆锥模型。设圆的半径为r，扇形的半径为R，则圆的半径与扇形的半径之间的关系为-------（ ）
A．R＝2r
B．R＝
r
C．R＝3r
D．R＝4r
3. 函数
的图象大致位置如图所示，则代数式
，
，
，
，
，
中，值为正数的有-----------------------------------（
）
A. 2个 B. 3个 C. 4个 D. 5个
4. 已知四边形
的两条对角线相等，但不垂直，顺次连结各边中点得四边形
，顺次连结
各边中点得四边形
，以此类推，则
为---------------------------------（
）
A．是矩形但不是菱形 B. 是菱形但不是矩形
C. 既是菱形又是矩形 D. 既非矩形又非菱形
5. 已知
、
均为质数，且满足
，则以
，
，
为边长的
三角形是----------------------------------------------------------------（ ）
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
6. 过点P(－1,3)作直线，使它与两坐标轴围成的三角形面积为5，这样的直线可以作（ ）
A. 4条 B. 3条 C. 2条 D. 1条
7. 有理数
，满足
，
，
，且
，则
的最大值是（ ）
A．1
B. 2
C. 3
D. 5
8. 如图，在2×3矩形方格纸上，各个小正方形的顶点称为格点，
则以格点为顶点的等腰直角三角形的个数为-----（ ）
A. 24 B. 38 C. 46 D. 50
二、填空题（每小题5分，共25分）
9. 盒子中有红球和白球各2个，小明把球从盒子中一个一个地摸出来，则红球和白球相间
出现（可以是“红白红白”也可以是“白红白红”）的可能性是 .
10. 如图所示，是用火柴棒摆成的一序列“井”字型图案，按这种方式摆下去，当每边上
摆201（即
）根时，需要的火柴棒的总根数是
根.
 |
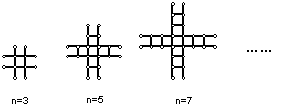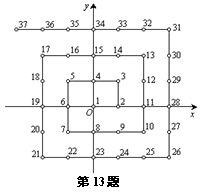
11. 如图，已知图中每个小方格的边长为1，则点C到AB所在直线的距离等于_______________.
 | |||||
 | |||||
 | |||||
12. 如图，在直径为6的半圆弧
上有两动点
、
，弦
、
相交于点
，
则
的值为___________________.
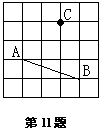
13. 把自然数按下图的次序排在直角坐标系中，每个自然数就对应着一个坐标. 例如1的对应点是原点（0，0），3的对应点是（1，1），16的对应点是（－1，2）,则2006的对应点的坐标是_____
三、解答题（本大题共35分）
14.（本题13分） 已知抛物线
(
,
是常数，
，
)的顶点是
，抛物线
的顶点是
.
（1）判断点是否在抛物线上，并说明理由.
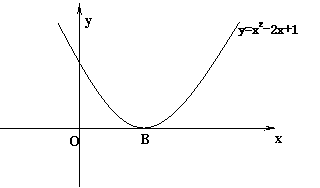（2）如果抛物线经过点，
①求的值；
②抛物线与
轴
的两个交点和它的顶点能否构成
直角三角形？若能，求出的值；
若不能，请说明理由.
15.（本题12分）
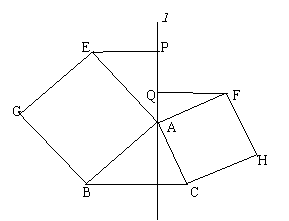
（1）如图，已知
， 以边，
为边分别向外作正方形
和
，直线l
为边
的垂线， 
于， 
于
求证：
（2）若以梯形
的两腰，
为边分别向外作正方形和
（如图所示），
设直线l为上底
的垂直平分线，于， 于，则
与
是否仍然
相等，说明你的理由.
16.（本题10分）已知方程
的根都是整数，求整数
的值.