2006年中考数学第一轮复习专题训练(九)
（立体图形的认识及角、相交线与平行线）
一、填空题：（每题 3 分，共 36 分）
１、32.43°＝＿＿＿度＿＿＿分＿＿＿秒。
２、若∠1＝30°，则∠A的补角是＿＿＿＿度。
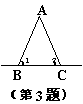
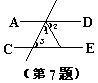
３、如图，∠1和∠2是直线AB、AC被BC所截而成的＿＿＿＿角。
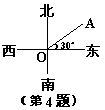
４、如图，射线OA表示的方向是＿＿＿＿＿＿＿。
５、锯木头时，一般先在木板上画出两个点，然后过这两点弹出一条墨线，这种做法的理由是＿＿＿＿＿＿＿＿＿＿＿＿＿＿。
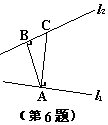６、如图，AC⊥l 1，AB⊥l 2，则点A到直线 l 2 的距离是指线段＿＿＿＿＿＿＿＿的长度。
７、如图，已知：AB∥CD，∠1＝∠2，若∠1＝50°，则∠3＝＿＿＿＿度。
８、如图，将两块直角三角板的直角顶点重合为如图所示的形状，若∠AOD＝127°，则∠BOC＝＿＿＿＿。
９、下面是一些相同的小正方体构成的几何体的三视图。
则至少要＿＿＿＿个正方体搭成。
主视图 左视图 俯视图
10、如图，要得到AB∥CD的结论，则需要角相等的条件是
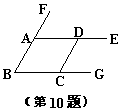＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿（写出一个即可）
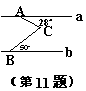
11、直线 a∥b，则∠ACB＝＿＿＿＿。
12、平面内有若干条直线，当下列情形时，可将平面最多分成几部分。
① 有一条直线时，最多分成两部分。
② 有两条直线时，最多分成 2＋2＝4 部分。
③ 有三条直线时，最多分成＿＿＿＿部分。
二、选择题。（每题 4 分，共 24 分）
１、在下列立体图形中，不属于多面体的是（ ）
A、正方体 B、三棱柱 C、长方体 D、圆锥
２、两条直线被第三条直线所截，则（ ）
A、同位角相等 B、同错角相等 C、同旁内角互补 D、无法确定
３、在修建泉厦高速公路时，有时需将弯曲的道路改直，根据（ ）
A、直线公理 B、直线公理或线段最短公理 C、线段最短公理 D、平行公理
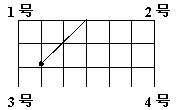
４、如图是一个台球桌面的示意图，如果一个球按图中所示的方向被击中（球可以经过多次反射），那么该球最后将落入的球袋是（ ）
A、1号袋 B、2号袋 C、3号袋 D、4号袋
５、下面图形中，不能折成正方体的是（ ）
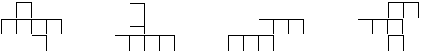
A B C D
６、如果两个角的一边在同一直线上，另一边互相平行，那么这两个角的关系是（ ）
A、相等 B、互补 C、相等或互补 D、相等且互补
三、解答题：（每题 8 分，共 40 分）
１、已知C为线段AB的中点，D在线段CB上，且DA＝6，DB＝4，求CD的长度。
 |
２、已知：一个角等于它的补角的
，求这个角的余角。
３、下列图形是某些立体图形的平面展开图，说出这些图形的名称。
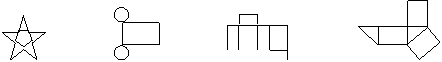
① ② ③ ④
①＿＿＿＿＿ ②＿＿＿＿＿ ③＿＿＿＿＿ ④＿＿＿＿＿
４、指出下列直观图对应的俯视图，在括号里填上对应的字母。
A B C D
（ ） （ ） （ ） （ ）
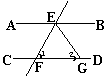５、如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF交CD于点G，∠1＝50°，求∠2的度数。
 |
四、（8分）将方格纸中的图形向右平行移动 4 格，再向下平移动 3 格，画出平移后的图形。
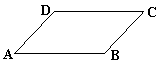
五、（8分）已知AB∥CD，∠A＝∠C，求证：∠B＝∠D。
 |
六、（10分）试计算，下午2点30分，钟表的时针与分针所形成的锐角为多少度。
七、（12分）如图是由五块积木搭成的，这几块积木都是相同的正方体，请你画出从这个图形的正面看、上面看、左面看的平面图。
 |
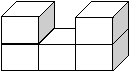八、（12分）如图，直线AB、CD相交于点O，OM⊥AB，NO⊥CD
①若∠1＝∠2，求∠AOD的度数。
②若∠1＝
∠BOC，求∠AOC和∠MOD。
 |
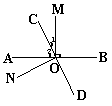答案：
（九）
一、1、32 25 48 2、150 3、同旁内 4、北偏东60° 5、过两点有且只有一条直线
6、AB 7、80° 8、53° 9、5 10、∠B＝∠DCG 11、78° 12、7
二、1、D 2、D 3、C 4、D 5、B 6、C
三、1、CD＝1 2、x＝
(180－x)
x＝30° 余角为60° 3、①五棱柱 ②圆柱 ③长方体
|
④三棱柱 4、D A B C 5、∠2＝65° 四、略
五、（注：题目改为求证：∠B＝∠D）解：∵AB∥CD ∴∠A＋∠D＝180°
∠B＋∠C＝180° 又∵∠A＝∠C ∴∠D＝∠B
六、105° 七、略
八、①∠AOD＝135° ②∠AOC＝60° ∠MOD＝120°