中考数学专题训练（十四） 三角函数与解直角三角形
一、选择题：
1．等腰三角形底边长为10㎝，周长为36cm，那么底角的余弦等于（ ）．
（A）
（B）
（C）
（D）
2．下列等式中正确的是（ ）
（A）
（B）cos30°+cos45°=cos75°
（C）
（D）2cot22°30＇=cot45°=1
3．△ABC中，
，则△ABC是（ ）
（A）等腰三角形 （B）等边三角形 （C）直角三角形 （D）等腰直角三角形
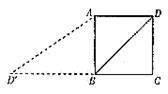4．如图，已知正方形ABCD的边长为2，如果将线段BD绕着点B旋转后，点D落在CB的延长线上的D′处，那么tan∠BAD′等于（ ）
(A)1 (B)
（C）
(D)
5．已知
，45°<α<90°，则cosα－sinα=（ ）
（A）
（B）
（C）
（D）
6．在Rt△ABC中，∠C=90°，a、b、c分别是∠A、∠B、∠C的对边，下列关系式中错误的是（ ）
（A）b=c·cosB （B）b=a·tanB （C）a=c·sinA （D）a=b·cotB
7．在Rt△ABC中，AD为斜边上的高，则下列结论中不成立的是（ ）
（A）
（B）
（C）
（D）
8．在△ABC中，三边之比为
，则sinA+tanA等于（ ）
（A）
（B）
（C）
（D）
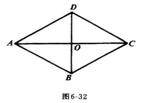
9．如图6-32，在菱形ABCD中，∠ADC=120°，则BD∶AC等于（ ）
（A）
（B）
（C）1∶2 （D）
10．如图，在四边形ABCD中，∠A=60°，∠B=∠D=90°，BC=2，
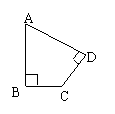CD=3，则AB=（ ）
（A）4 （B）5 （C）
（D）
11．如图是一束平行的光线从教室窗户射入的平面示意图，光线与地面所成的∠AMC=
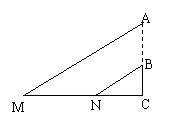30°，在教室地面的影长MN=米，若窗户的下檐到教室地面的距离BC=1米，则窗户的上檐到教室地面的距离AC为（ ）
（A）米 （B）3米 （C）3.2 米 （D）米
12．如图1，梯形护坡石坝的斜坡
的坡度
1:3，坝高
为2米，则斜坡的长是
（ ）
A．
B．
C．
D．
13．如图，在等腰三角形中，∠C=90°，AC=6，D是AC上一点，
若
∠DBA=
，则AD的长是（ ）
(A) (B)
2 （C）1
(D)
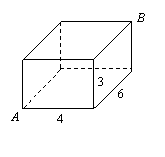14．如图是一块长、宽、高分别是6cm,4cm和3cm的长方体木块.一只蚂蚁要从长方体木块的一个顶点
处，沿着长方体的表面到长方体上和相对的顶点
处吃食物，那么它需要爬行的最短路径的长是
（ ）
(A)
（
）
(B) 
(C) 
(D)
15．如图，在一个房间内，有一个梯子斜靠在墙上，梯子顶
端距地面的垂直距离MA为a米，此时梯子的倾斜角为75°.若梯子底
端距离地面的垂直距离NB为b米，梯子的倾斜角为45°.则这间房子
的宽AB是（ ）
（A）
米 （B）
米 （C）b米 （D）a米
二、填空题：
１．锐角Ａ满足２
(Ａ－１５０)＝
则∠Ａ＝______________.
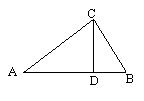
２．如图，CD
是Rt△ABC斜边上的高线，若
，
BD=1，则AD=________.
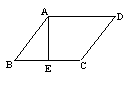3．如图，在菱形ABCD中，AE⊥BC于E，已知EC=1，
，
则这个菱形的面积是________________.
4．某人欲以最短距离游泳横渡一条河，由于水流的影响，实际上岸地点Ｃ偏离欲到达点Ｂ约200米，结果他在水中实际游乐520米，则该河流的 宽度约为___________.
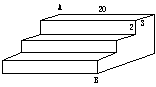5.如图是一个三级台阶，它的每一级的长宽和高分别为20dm、3dm、
2dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B
点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短
路程是_____________.
三、解答题：
1。计算：（1）2sin30°+3tan30°+cot45° (2)sin45°+tan60°cos30°
(3)
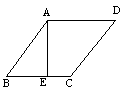
2．如图所示，在菱形ABCD中，
于E点，EC=1，
，求四边形AECD的周长。
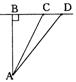
3．如图某校A与直线公路距离为3000米，又与该公路上某车站D的距离为5000米，现要在公路边建一个小商店C，使之与学校A及车站D的距离相等，那么，该店与车站D的距离是多少米？
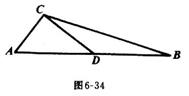
4．如图在△ABC中，点D是AB的中点，DC⊥AC，且
，求∠A的四个三角函数值。
 |
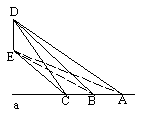
5．直线a和水塔底面E在同一水平面上，在直线a上的三个点A、B、C处分别测得塔顶D的仰角为
，同时量得
米，求塔高DE多少米？（结果保留根号）
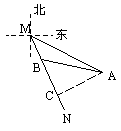
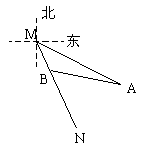
6．如图所示，MN表示某引水工程的一段设计路线，从M到N的走向为南偏东
，在M的南偏东
方向上有一点A，以A为圆心，500米为半径的圆形区域为居民区，则MN上另一点B，测得BA的方向为南偏东
。已知
米，通过计算回答，如果不改变方向，输水路线是否会穿过居民区？
答案：
一选择题：（1）A (2) A (3) C （4）B (5) B (6) A （7）D （8）A（9）B （10）D （11）B （12 B （13）D （14）B （15）D
二填空题：（1） 75° (2) 2 (3) 
（4） 480米 (5)25dm
三解答题：1．（1） 
（2）
（3） 
2。52
3．3125米 4、
5．解：设塔高为h米
在
中得
又在
中，由，得
∴
于是，得
（米）
∴该水塔高
米。
6. 过A作
于C设
，
∴
，
又∵
∴
∴不改变方向输水线路不会穿过居民区
