2005年河南省高级中等学校招生统一考试试卷 数学 姓名 分数
注意事项：
1.本试卷三大题，满分100分，考试时间100分钟，请用钢笔或圆珠笔直接答在试卷上。
2.答题前将密封线的项目填写清楚。
| 题号 | 一 | 二 | 三 | 总分 | ||||||||
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 分数 | ||||||||||||
一、选择题（每小题3分，共18分）下列各小题均有四个答案，其中只有一个是正确的，请将正确答案的代号字母填入题后括号内
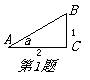
1．tan a等于【 】A.
B. 
C. 
D.2
2.如图所示，两温度计读数分别为我国某地今年2月份某天的最低气温与最高气温，
那么这天的最高气温比最低气温高【 】
A.5°C B.7°C C.12°C D.-12°C
3.在一次科学探测活动中，探测人员发现一目标在如图所示的阴影区域内，则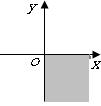
目标的
坐标可能是【 】A.（-3,300） B.（7,-500） C.（9,600） D.（-2,-800）
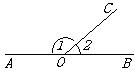
4.如图，点O在直线AB上，OC为射线,∠1比∠2的3倍少10°，设∠1、∠2
的度数分别是x、y,那么下列可以求出这两个角的度数的方程组是【 】
A.
B. 
C. 
D. 
5.下列各数中，适合方程
的一个近似值（精确到0.1）是
【 】 A.1.5 B.1.6 C.1.7 D.1.8
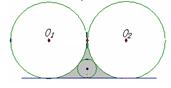6.如图，半径为4的两等圆相外切，它们的一条外公切线与两圆围成的阴影部分中，存在的最大圆的半径等于【 】A.1/2 B.2/3 C.3/4 D.1
二、填空题（每小题3分，共21分）
7.计算
。
8.函数
中，自变量x的取值范围是 。
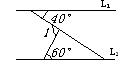
9.如图所示，L1∥L2,则∠1＝ 度。
10.点（-1，-1） （填：“在”与“不在”）直线y=-2x-3上。
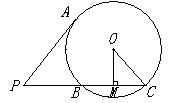
11.如图，已知PA为⊙O的切线，PBC为⊙O的割线，PA=
,PB=BC,
⊙O的半径OC=5,那么弦BC的弦心距OM＝ 。 11题图
12.从《中华人民共和国2004年国民经济和社会发展统计公报》中获悉，2004年末国家全年各项税收收入25718亿元，用科学记数法表示为 元（保留三个有效数字）。
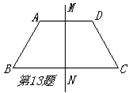13.如图，梯形ABCD中，AD∥BC,AB=CD=AD=1,∠B=60°,直线MN为梯形
ABCD的对称轴，P为MN上一点，那么PC+PD的最小值为 。
三、解答题（本大题9个小题，共61分）
14.（5分）化简：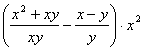
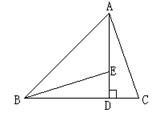
15.（5分）如图：△ABC中，∠ABC＝45°，AD⊥BC于D,点E在
AD上，且DE=CD.求证：BE=AC.
16.（6分）观察下表，填表后再解答问题：
（1）完成下列表格：
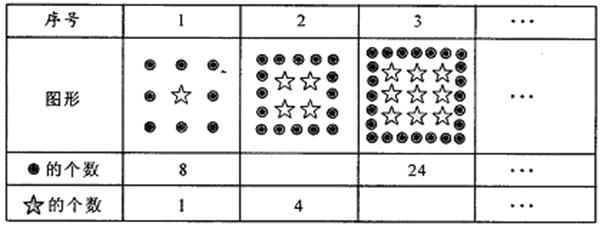
（2）试求第几个图形中的“⊙”和“★”的个数相等？
17.(6分)已知x1、x2是一元二次方程2x2－2x＋1－3m＝0的两个实数根，且x1、x2满足不等式x1·x2＋2（x1＋x2）＞0，求实数m的取值范围.
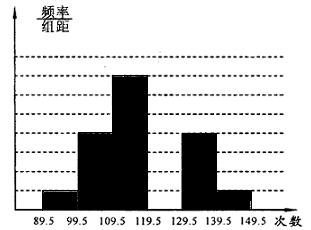18.（6分）小明在一份题目为“了解本校初三毕业生体能情况”的调查报告中，通过对部分学生一分钟跳绳次数成绩的整理与计算，得出89.5～99.5组的频率为0.04，且绘出如下频率分布直方图（规定一分钟110次或110次以上为达标成绩）：
（1） 请补上小明同学漏画的119.5～129.5的
频率直方图.
（2） 小明所调查学生的达标率为
（3） 根据以上信息，替小明写出一条调查结论。
结论：
.
19（6分）已知⊙O的内接四边形ABCD中，AD∥BC.试判断四边形ABCD的形状，并加以证明。
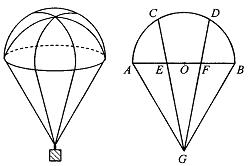
20.（7分）空投物资用的某种降落伞的轴截面如右图所示，△ABG是等边三角形，C、D是以AB为直径的半圆O的两个三等分点。CG、DG分别交AB于点E、F.试判断点E、F分别位于所在线段的什么位置？并证明你的结论.（证一种情况即可）
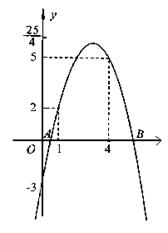
21.（9分）已知一个二次函数的图像过如图所示三点.
（1）求抛物线的对称轴；
（2）平行于x轴的直线L的解析式为y＝
，抛物线与x轴交于A、B两点.在抛物线的对称轴上找P，使BP的长等于直线L与x轴间的距离.求P的坐标.
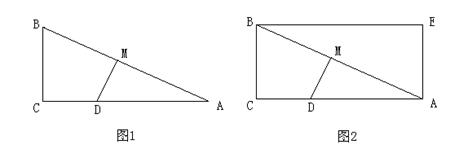
22.（11分）如图1，Rt△ABC中，∠C＝90°，AC＝12，BC=5,点M在AB上，且AM＝6.
（1）动点D在边AC上运动，且与A、C均不重合，设CD＝x.
①设△ABC与△ADM的面积之比是y，求y与x之间的函数关系式（写出自变量x的取值范围）；
②当x取何值时，△ADM是等腰三角形？写出你的理由.
（2）如图2，以图1中的BC、CA为一组邻边的矩形ACBE中，动点D在矩形边上运动一周，能使△ADM是以∠AMD为顶点的等腰三角形共有多少个（直接写结果，不要求说明理由）？
