常州市2005年初中毕业、升学统一考试
数学试题参考答案及评分标准
一、填空题（每个空格1分，共18分）
1、
; 2、1 ，4 ； 3、1.3×109 ;
4、0.5736 , 6.403;
5、90，2 ； 6、
，8 ； 7、
8、x=3 ， 1＜x＜5 ，上 ，4
二、选择题（本大题共9小题，每小题2分，共18分）
| 题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 答案 | C | D | C | C | B | D | A | B | A |
三、解答题（第18题10分，第19题8分，共18分）
18、解：（1）原式=
……………………………………4分
=
………………………………………………5分
（2）原式=
…………………………………2分
=
…………………………………………4分
=
………………………………………………5分
19、解：（1）去分母，得 x=3（x-2）……………………………………1分
解得， x=3…………………………………………2分
经检验： x=3是原方程的根.……………………3分
∴原方程的根是x=3 4分
（2）
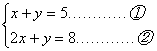
②－①，得x=3………………………………………………2分
把x=3代入①，得3＋y=5 ， ∴y=2………………………3分
∴方程组的解为
………………………………………4分
四、解答题（第20题5分，第21题7分，共12分）
20、证明：∵DE∥BC,EF∥AB,
∴四边形BDEF是平行四边形 2分
∴DE=BF 3分
∵F是BC的中点
∴BF=CF 4分
∴DE=CF 5分
21、解：（1）图中还有相等的线段是：AE=BF=CD，AF=BD=CE 2分
事实上，∵△ABC与△DEF都是等边三角形，
∴∠A=∠B=∠C=60°，∠EDF=∠DEF=∠EFD=60°,DE=EF=FD 3分
又∵∠CED+∠AEF=120°，∠CDE+∠CED=120°
∴∠AEF=∠CDE，同理，得∠CDE=∠BFD， 4分
∴△AEF≌△BFD≌△CDE（AAS），
所以AE=BF=CD，AF=BD=CE 5分
（2）线段AE、BF、CD它们绕△ABC的内心按顺时针（或按逆时针）方向旋转120°，可互相得到，线段AF、BD、CE它们绕△ABC的内心按顺时针（或按逆时针）方向旋转120°,可互相得到。 7分
注：其他解法，按以上标准相应给分。
五、解答题（第22题8分，第23题7分，共15分）
22、答：（1）第一次； 2分
（2）第二次； 4分
（3） 第一次分数的中位数在20~39分数段 6分
第二次分数的中位数在40~59分数段 8分
23、解：方法不公平。
说理方法一：用表格来说明，
| 红球 白球 | 1 | 2 | 3 |
| 1 | （1，1）（2） | （1，2）（3） | （1，3）（4） |
| 2 | （2，1）（3） | （2，2）（4） | （2，3）（5） |
| 3 | （3，1）（4） | （3，2）（5） | （3，3）（6） |
说理方法二：用树状图来说明：
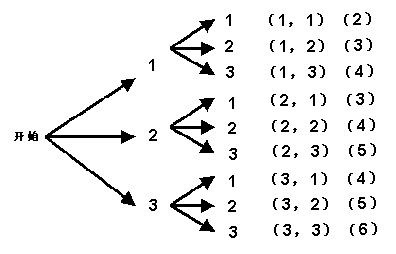
所以，七（2）班被选中的概率为
，七（3）班被选中的概率为
，七（4）班被选中的概率为
，七（5）班被选中的概率为，七（6）班被选中的概率为， 5分
所以，这种方法不公平 7分
六、画图与说理（第24题6分，第25题6分，共12分）
24、解：图不唯一 ，略 。第（1）题2分；第（2）题4分。
25、解：
画图正确 4分
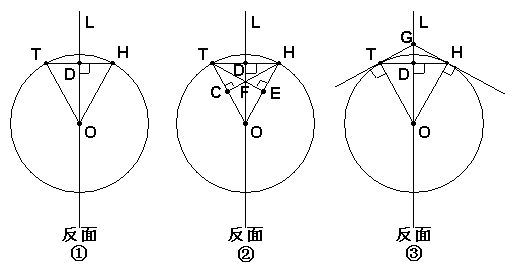
方法一：如图①，画TH的垂线L交TH于D，则点D就是TH的中点。
依据是垂径定理。 5分
方法二：如图②，分别过点T、H画HC⊥TO，TE⊥HO，HC与TE相交于点F，过点O、F画直线L交HT于点D，则点D就是HT的中点。
由画图知，Rt△HOC≌Rt△TOE，易得HF=TF，又OH=OT
所以点O、F在HT的中垂线上，所以HD=TD 6分
方法三：如图③，（原理同方法二） 6分
注：其它解法，按以上标准相应给分
七、解答题（第26题7分，第27题8分，第28题12分，共27分）
26、解：（1）由题意得：
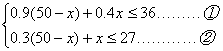2分
由①得，x≥18，由②得，x≤20，
所以x的取值得范围是18≤x≤20（x为正整数） 4分
（2）制作A型和B型陶艺品的件数为：
①制作A型陶艺品32件，制作B型陶艺品18件； 5分
②制作A型陶艺品31件，制作B型陶艺品19件； 6分
③制作A型陶艺品30件，制作B型陶艺品20件； 7分
27、解：本题共有4种情况。
如图①，过点A做AD⊥BC于D
则AD=ABsin60°=
，∴点A的纵坐标为
1分
将其代入y=
，得x=2，即OD=2
2分
在Rt△ADC中，DC=
，所以OC=
，
即点C1的坐标为（
）
3分
（2）如图②，过点A作AE⊥BC于E
则AE=，OE=2，CE=，所以OC=
4分
即点C2的坐标为（，0）
5分
根据双曲线的对称性，得点C3的坐标为（
）
6分
点C4的坐标为（
）
7分
所以点C的坐标分别为：（）、（，0）、（）、（）
28、（1）CD与⊙O相切。 1分
因为A、D、O在一直线上，∠ADC=90°，
所以∠COD=90°，所以CD是⊙O的切线 3分
CD与⊙O相切时，有两种情况：①切点在第二象限时（如图①），
设正方形ABCD的边长为a，则a2＋（a＋1）2=13，
解得a=2，或a=-3（舍去） 4分
过点D作DE⊥OB于E，则Rt△ODE≌Rt△OBA，所以
，所以DE=
，
OE=
，所以点D1的坐标是（-，）
5分
所以OD所在直线对应的函数表达式为y=
6分
②切点在第四象限时（如图②），
设正方形ABCD的边长为b，则b2＋（b－1）2=13，
解得b=-2（舍去），或b=3 7分
过点D作DF⊥OB于F，则Rt△ODF∽Rt△OBA，所以
，所以OF=，DF=，所以点D2的坐标是（，-）
8分
所以OD所在直线对应的函数表达式为y=
9分
（2）如图③，
过点D作DG⊥OB于G，连接BD、OD，则BD2=BG2＋DG2=（BO－OG）2＋OD2-OG2=
10分
所以S=AB2=
11分
因为-1≤x≤1，所以S的最大值为
，
S的最小值为
12分