2005年杭州市各类高中招生考试
数学模拟卷（一）
（满分：120分，时间：100分钟）
一、选择题（本题有15小题，每小题3分，共45分）
1． 下列计算：①
，②
，③
，④
，
⑤
，正确的有
（A）2个 （B）3个 （C）4个 （D）5个
2． 杨利伟乘坐“神州”五号载人飞船旅游太空，行程约600000千米，用科学记数法表示是
（A）
千米 （B）
千米 （C）
千米 （D）
千米
3． 小明参加文学知识竞赛，共有20个必答题，答对1题得5分，
答错1题倒扣5分，小明要力争超过80分，最多只能答错
（A）1题 （B）2题 （C）3题 （D）4题
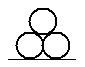
4． 直径为d的三个水泥管堆放成如图形状，最高点离地面的高度为 （第4题）
（A）
（B）
（C）
（D）
5． 3本小说，5本科技书和2本诗集，分类放在书架上，任
意抽取紧挨着的2本书，这2本书是同一类的概率等于 （第5题）
（A）
（B）
（C）
（D）
6． 在一条长为40厘米的木板上要打10个直径为3厘米的圆孔，木板两端到圆孔边缘的距离和相邻圆孔边缘的距离都相等，设相邻两孔的圆心距为x厘米，正确的方程是
（A）
（B）
（C）
（D）
（第6题）
7． 为了了解初三学生的数学学习水平，举行测试，抽取其中30份试卷进行分析. 在这个问题中，样本是
（A）30位学生 （B）30份试卷 （C）30份试卷的解答水平 （D）30
8． 对于函数
，下列判断：① y < 0，② y随x的增大而增大，③图象
与曲线
关于x轴对称，④ 图象关于直线
对称，正确判断有
（A）1个 （B）2个 （C）3个 （D）4个
9． 如图，延长⊙O的直径AB到D，使BD=OB，DC是⊙O的
切线，则cos∠D等于
（A）
（B）
（C）
（D）
（第9题）
10．下图是某企业2001～2004年的产值统计图，每年产值的平均增长率等于
（A）33%
（B）35% （C）41%
（D）59%
（第10题） （第11题） （第12题）
11． 把边长为4的正方形ABCD的顶点C折到AB的中点M，折痕EF的长等于
（A）
（B）
（C）
（D）
12．已知抛物线
如图所示，请判断关于x的方程
的根的情况，正确的判断是
（A）有两个不相等的正实根 （B）有两个异号的实数根
（C）有两个相等的实数根 （D）没有实数根
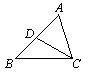
13．如图，D是AB的中点，如果△ABC ～△ACD，那么
=
（第13题）
（A）
（B）
（C）
（D）
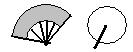
14．纸扇的扇面是扇环，大小弧的半径分别为30厘米和15厘米，
圆心角为120°；绢扇的扇面是直径为30厘米的圆.这两种 （第14题）
扇子的扇面面积
（A）纸扇较大 （B）绢扇较大 （C）相同 （D）不能比较
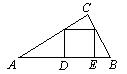15．如图，把一个正方形内接与Rt△ABC中，使正方形的顶点D，
E在AB上，其余两个顶点分别在两条直角边上，设BC=a，
AC=b，则AD：DE：EB=
（A）
（B）
（C）
（D）
（第15题）
二、填空题（本题有5小题，每小题4分，共20分）
16．一件服装的标价为600元，商家要确保赢利20%，因此最多只能8折销售，那么这件服装的进价是 ▲ 元.
17．已知实数a，b，c满足
，则a＋b＋c = ▲ .
18．边长为4的两个正方形重合，把上面一个正方形绕中心旋转45°，重叠部分（图中阴影）就成为一个正8边形，这个正8边形的边长等于 ▲ .
 |
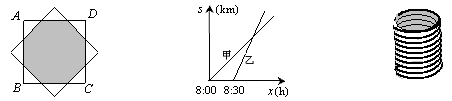（第18题） （第19题） （第20题）
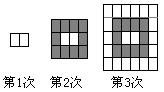
19．甲、乙两人驱车从杭州出发到南京，他们出发的时刻、行驶的里程s与时刻x的函数图象如图所示，若甲12：10到达南京，比乙晚了半小时，则乙超过甲的时刻是 ▲ .
20．一个圆柱形的弹簧直径1厘米，高4厘米，钢丝刚好绕成10匝，则绕成弹簧的钢丝长约等于 ▲ 厘米（精确到1厘米）.
三、解答题（本题有6小题，共55分）
21．（7分）化简并求值：
，其中
.
22．（8分）新建体操房的地面铺木地板，每块地板为长方形，
工人从中间铺起，第1次铺2块（图1）；第2次把第1
次铺成的地板围起来（图2）；第3次又把前两次铺成的
地板围起来（图3）；用这样的顺序继续铺下去……问：
（1）铺完第n次一共用了几块木地板？
（2）当一共铺了500块木地板时，正轮到铺第几次？ （第22题）
23．（8分）解方程组：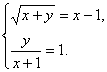
24．（10分）如图，抛物线
与y轴相交于点C，
与直线y = x相交于两点A，B，且OA=OB，已知AC平行
与x轴，求这条抛物线的解析式. （第24题）
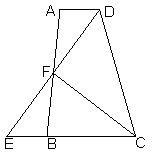
25．（10分）
如图在梯形ABCD中，AD//BC，F是AB中点，DF、CB的延长线相交于E，CD=CE
（1）求证：
（2）若
，AB=c，CD=d，求证AD、BC的长是方程
的两根
（第25题）
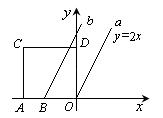
26．（12分）在如图的直角坐标系中，正方形OACD的边长
为10，点B的横坐标为－6，直线a∥b，且直线a的解
析式为y=2x. 现使正方形OACD沿着x轴以每秒1个单
位的速度向右平移. 设在平移中t秒时正方形夹在直线a，
b之间的部分面积为S. （第26题）
（1）当
时，求S与t的函数解析式；
（2）在的范围内，S是否有最大值？如果有最大值，请求出最大值，否则请说明理由.