专题训练二：阅读理解题
班级：_________ 姓名：_________ 得分：_________
一、填空题(1、2每小题5分，3小题7分，4小题3分，5小题6分，6小题4分，共30分)
1．(2002年龙岩市)阅读下面材料并完成填空．
你能比较两个数20012002和20022001的大小吗？为了解决这个问题，先把问题一般化，即比较nn＋1和(n＋1)n的大小(n≥1的整数)．然后，从分析n＝1，n＝2，n＝3，……，这些简单情形入手，从中发现规律，经过归纳，猜想出结论．
(1)通过计算，比较下列①～③各组两个数的大小(在横线上填“＞”“＜”或“＝”)
①12______21； ②23______32； ③34______43；
④45＞54； ⑤56＞65； ⑥67＞76； ⑦78＞87；…
(2)从第(1)小题的结果经过归纳，可以猜想出nn＋1和(n＋1)n的大小关系是：_________．
(3)根据上面归纳猜想得到的一般结论，可以得到20012002______20022001(填“＞”“＜”或“＝”)．
2．阅读下列课文中某一例题及解答过程的摘录：
“已知方程x2-2x-1＝0，求一个一元二次方程，使它的根是原方程的各根的立方．”
解：设方程x2-2x-1＝0的两根是x1、x2，那么所求的方程的两根是x13、x23．
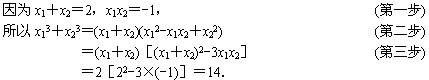
x13·x23＝(x1x2)3＝(-1)3＝-1．
请你回答：
(1)得到“第一步”式子的根据是______．
(2)得到“第二步”式子所使用的具体公式是______．
(3)得到“第三步”的中括号内的式子所使用的具体方法是______．
(4)作“第三步”变形的具体目的是______．
(5)原题最后求得的方程是______．
3．先阅读下列(1)题然后解答(2)、(3)题：
(1)用分组分解法分解多项式：mx＋nx＋my＋ny＝(mx＋nx)＋(my＋ny)，组内公因式分别为x、y，组间公因式为m＋n，最后分解结果为：(m＋n)(x＋y)
(2)也可以这样分解：mx＋nx＋my＋ny＝(______)＋(______)，组内公因式分别为______，组间公因式为______，最后分解结果为：______．
(3)上述两种分组的目的都是______，分组分解的另一个目的是分组后能运用公式法分解．请你设计一个关于字母x、y的二次四项式因式分解，要求要用到分组分解法和完全平方公式：_________．
4．阅读下面一题的解题过程，请判断是否正确，若不正确，请写出正确的解答．
已知a为实数，化简
．
解：
-a·
＝(a-1)·
答：____________
5．阅读下列证明过程：
已知，如图1四边形ABCD中，AB＝DC，AC＝BD，AD≠BC，求证：四边形ABCD是等腰梯形．
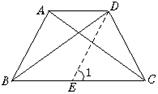
图1
读后完成下列各小题．
(1)证明过程是否有错误？如有，错在第几步上，答：_________．
(2)作DE∥AB的目的是：__________．
(3)有人认为第9步是多余的，你的看法呢？为什么？答：________．
(4)判断四边形ABED为平行四边形的依据是：_________．
(5)判断四边形ABCD是等腰梯形的依据是__________．
(6)若题设中没有AD≠BC，那么四边形ABCD一定是等腰梯形吗？为什么？答______．
6．(2002年鄂州市)从A、B、C 3人中选取2人当代表有A和B、A和C、B和C 3种不同的选法，抽象成数学模型是：从3个元素中选取2个元素的组合，记作
＝3．一般地，从m个元素中选取n个元素的组合，记作
．根据以上分析，从6人中选取4人当代表的不同选法有______种．
二、选择题(每小题5分，共10分)
7．(2002年扬州市)计算机是将信息转换成二进制数进行处理的，二进制即“逢2进1”，如(1101)2表示二进制数，将它转换成十进制形式是1×23＋1×22＋0×21＋1×20＝13，那么将二进制(1111)2转换成十进制形式是数( )
A．8 B．15 C．20 D．30
8．(2002年威海市)如果一个图形绕一个定点旋转一个角a (0°＜a ≤180°)，能够与原来的图形重合，那么这个图形就叫做旋转对称图形．例如，正三角形绕着它的中心旋转
120°(如图2)，能够与原来的正三角形重合，因而正三角形是旋转对称图形．图3是一个五叶风车的示意图，它也是旋转对称图形(a ＝72°)．
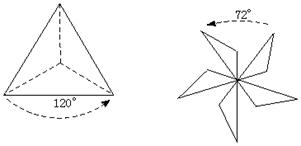
图2 图3
显然，中心对称图形都是旋转对称图形，但旋转对称图形不一定是中心对称图形．下面四个图形中，是旋转对称图形的有( )
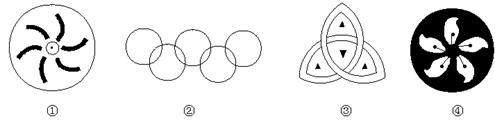
A．①②③ B．②③④
C．①③④ D．①②③④
三、解答题(每小题10分，共60分)
9．请先阅读下列文字，然后解答：
初中数学课本有这样一段叙述：“要比较a与b的大小，可先求a与b的差，再看这个差是正数、负数还是零．”由此可见，要判断两个代数式值的大小，只要考虑它们的差就可以．
问题：甲乙两人两次同时在同一粮店购买粮食(假设两次购买粮食的单价不相同)，甲每次购买粮食100千克，乙每次购买粮用去100元．
(1)假设x、y分别表示两次购粮的单价(单位：元/千克)．试用含x、y的代数式表示：甲两次购买粮食共需付款______元；乙两次共购买______千克的粮食．若甲两次购粮的平均单价为每千克q 1元，乙两次购粮的平均单价为每千克q 2元，则q 1＝______，q 2＝______．
(2)若规定：谁两次购粮的平均单价低，谁的购粮方式就更合算，请你判断甲、乙两人的购粮方式哪一个更合算些，并说明理由．
10．阅读下面的短文，并解答下列问题：
我们把相似形的概念推广到空间：如果两个几何体大小不一定相等，但形状完全相同，就把它们叫做相似体．
如图4，甲、乙是两个不同的正方体，正方体都是相似体，它们的一切对应线段之比都等于相似比(a∶b)．
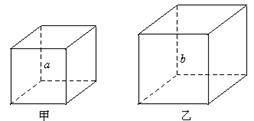
图4
设S甲、S乙分别表示这两个正方体的表面积，则
又设V甲、V乙分别表示这两个正方体的体积，则
(1)下列几何体中，一定属于相似体的是( )
A．两个球体 B．两个锥体
C．两个圆柱体 D．两个长方体
(2)请归纳出相似体的三条主要性质：①相似体的一切对应线段(或弧)长的比等于______；②相似体表面积的比等于______；③相似体体积比等于______．
(3)假定在完全正常发育的条件下，不同时期的同一人的人体是相似体，一个小朋友上幼儿园时身高为1.1米，体重为18千克，到了初三时，身高为1.65米，问他的体重是多少？(不考虑不同时期人体平均密度的变化)
11．(2002年大连市)阅读材料，解答问题．
阅读材料：
当抛物线的解析式中含有字母系数时，随着系数中的字母取值的不同，抛物线的顶点坐标也将发生变化．
例如：由抛物线y＝x2-2mx＋m2＋2m-1，①
有y＝(x-m)2＋2m-1，②
∴ 抛物线的顶点坐标为(m，2m-1)．
当m的值变化时，x、y的值也随之变化．因而y值也随x值的变化而变化．
将③代入④，得y＝2x-1．⑤
可见，不论m取任何实数，抛物线顶点的纵坐标y和横坐标x都满足关系式：y＝2x-1．
(1)在上述过程中，由①到②所用的数学方法是______，其中运用了______公式．由③、④得到⑤所用的数学方法是______；
(2)根据阅读材料提供的方法，确定抛物线y＝x2-2mx＋2m2-3m＋1顶点的纵坐标y与横坐标x之间的关系式．
12．(2002年威海市)某村实行合作医疗制度，村委会规定：
(一)每位村民年初缴纳合作医疗基金a元；
(二)村民个人当年治病花费的医疗费(以医院的收据为准)，年底按下列办法处理：
| 村民个人当年花费的医疗费 | 医疗费的处理办法 |
| 不超过b元的部分 | 全部由村集体承担(即全部报销) |
| 超过b元不超过5000元的部分 | 个人承担c%，其余部分由村集体承担 |
| 超过5000元的部分 | 全部由村集体承担 |
设一位村民当年治病花费的医疗费为x元，他个人实际承担的医疗费用(包括医疗费中个人承担的部分和缴纳的合作医疗基金)为y元．
(1)当0≤x≤b时，y＝a；当b＜x≤5000时，y＝______(用含有a、b、c、x的式子表示)．
(2)下表是该村4位村民2001年治病花费的医疗费和个人实际承担的费用．根据表格中的数据，求a、b、c，并且求当b＜x≤5000时，函数y的解析式．
| 村民 | 治病花费的医疗费x(元) | 个人实际承担的费用y(元) |
| 甲 | 20 | 30 |
| 乙 | 40 | 30 |
| 丙 | 90 | 50 |
| 丁 | 150 | 80 |
(3)村民个人一年最多承担医疗费用多少元？
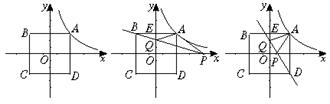
13．(2002年昆明市)已知矩形ABCD的面积为36，以此矩形的对称轴为坐标轴建立平面直角坐标系，设点A的坐标为(x，y)，其中x＞0，y＞0．
(1)求出y与x之间的函数关系式，求出自变量x的取值范围；
(2)用x、y表示矩形ABCD的外接圆的面积S，并用下列方法，解答后面的问题：
方法：∵ a2＋
＋2k(k为常数且k＞0，a≠0)，(a-
)2≥0，∴ a2＋
≥2k．
∴ 当a-＝0，即a＝±
时，a2＋取得最小值2k．
问题：当点A在何位置时，矩形ABCD的外接圆面积S最小？并求出S的最小值；
(3)如果直线y＝mx＋2(m＜0)与x轴交于点P，与y轴交于点Q，那么是否存在这样的实数m，使得点P、Q与(2)中求出的点A构成△PAQ的面积是矩形ABCD面积的
？若存在，请求出m的值；若不存在，请说明理由．
14．(2002年临沂市)九年义务教育三年制初级中学《几何》第二册第180页第2题：
A、B两点被池塘隔开，在AB外选一点C，连结AC和BC，并分别找出AC和BC的中点M、N，如果测得MN＝20 m，那么AB＝2×20 m＝40 m．
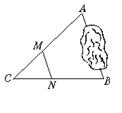
图5
(1)也可由图6所求，用相似三角形知识来解，请根据题意填空：延长AC到D，使CD＝
AC，延长BC到E，使CE＝______，则由相似三角形得，AB＝______．
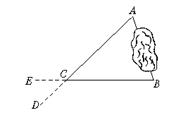
图6
(2)还可由三角形全等的知识来设计测量方案，求出AB的长，请用上面类似的步骤，在图7中画出图形并叙述你的测量方案．
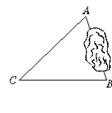
图7
15．(2002年深圳市)阅读材料，解答问题．
命题：如图8在锐角△DBC中，BC＝a，CA＝b，AB＝c，△ABC的外接圆半径为R．则
＝2R．
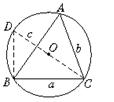
图8
证明：连结CO并延长交⊙O于点D，连结DB，则∠D＝∠A．
∵ CD为⊙O的直径，∴ ∠DBC＝90°．
在Rt△DBC中，
∵ sinD＝
，∴ sinA＝
，即
＝2R．
同理
＝2R，
＝2R．
∴ 
．
请你阅读前面所给的命题及其证明后，完成下面的(1)、(2)两小题．
(1)前面的阅读材料中略去了“＝2R和＝2R”的证明过程，请你把“＝2R”的证明过程补写出来．
(2)直接用前面阅读材料中命题的结论解题．
已知：如图10，在锐角△ABC中，BC＝
，CA＝
，∠A＝60°，求△ABC的外接圆半径R及∠C．
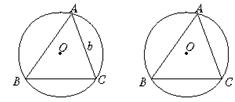
图9 图10
16．(2001年咸宁市)已知下面各图形被一条直线将其面积平分：
略解 由图11可知经过圆的圆心的直线或经过平行四边形的中心的直线平分其面积，据其在图12中作连接其中心的直线即可．(图略)
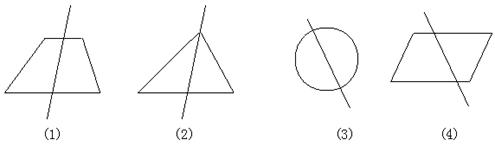
图11
观察以上图形，用所得的结论或启示对下面每个图形作一条直线将其阴影部分的面积平分．(不写画法，不证明，保留作图痕迹)．
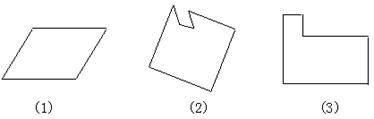
图12
参考答案
一、1．(1)＜ ＜ ＞ (2)nn＋1＜(n＋1)n(n≤2) nn＋1＞(n＋1)n(n≥3) (3)＞
2．(1)一元二次方程根与系数的关系； (2)立方和公式； (3)配方法； (4)使用“第一步”所得的结果； (5)y2-14y-1＝0
3．(2)mx＋my nx＋ny m、n (x＋y) (x＋y)(m＋n)；
(3)提取公因式；如1-x2＋2xy-y2＝1-(x2-2xy＋y2)＝1-(x-y)2＝(1＋x-y)(1-x＋y)
4．∵ a＜0，
∴ 
＋a·
·
．
5．(1)没有错误； (2)为了证明AD∥BC； (3)并不多余； (4)一组对边平行且相等的四边形是平行四边形； (5)梯形及等腰梯形的定义； (6)不一定，因为当AD＝BC时，四边形ABCD是矩形．
6．15
二、7．B 8．C
三、9．(1)100x＋100y；
；q 1＝
，q 2＝
；
(2)∵ q 1-q 2＝
，
∵ x＞0，y＞0，且x≠y，
∴ q 1-q 2＞0．∴ q 1＞q 2．
∴ 甲的购粮方式更合算．
10．(1)A；
(2)①相似比，②相似比的平方，③相似比的立方；
(3)设他的体重为x千克，根据题意得
解得x＝60.75(千克)
答：他的体重是60.75千克．
11．(1)配方法、完全平方法、消元法
(2)y＝x2-2mx＋2m2-3m＋1＝x2-2mx＋m2＋m2-3m＋1＝(x-m)2＋m2-3m＋1
∴ 该抛物线顶点坐标为(m，m2-3m＋1)
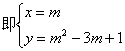
将①代入②，得y＝x2-3x＋1．
∴ 所给抛物线顶点的纵坐标y与横坐标x的关系式为y＝x2-3x＋1．
12．(1)y＝(x-b)c%＋a
(2)甲、乙两人花费的医疗费不同，但实际承担的费用相同(都是30元)，说明他们两人花费的医疗费都不超过b元，因此，他们实际承担的费用就是缴纳的合作医疗基金，即a＝30．丙、丁两人实际承担的医疗费用超过了30元，说明他们一年的医疗费超过了b元，但不足5000元．所以
，解这个方程组，得b＝50，c＝50，∴ 当b＜x≤5000时，y＝(x-50)·50%＋30．即y＝x＋5．
(3)将x＝5000代入y的解析式，得y＝5000×0.5＋5＝2505．
∴ 村民个人一年最多承担医疗费2505元．
13．建立平面直角坐标系，(1)根据题意可知：xy＝9，∴ y与x之间的函数关系式是y＝
，自变量x的取值范围是x＞0．
(2)S＝p(x2＋y2)，∵ x2＋y2＝x2＋()2≥18，当且仅当x-＝0，即x＝3时，S最小＝18p．此时，y＝＝3，所以当点A的坐标为(3，3)时，矩形的外接圆面积S最小，S的最小值为18p．
(3)存在，如图，设AB与y轴相交于点E，由已知得：A(3，3)，Q(0，2)，P(-
，0)，∴ S△PAQ＝S梯形APOE-S△AEQ-S△OPQ＝［(-＋3)×3-1×3-2×(-)］＝3-
．
∴ 3-＝×36．解得：m＝-
．
14．(1)BC 2ED
(2)延长AC至D，使AC＝CD，延长BC至E，使BC＝EC，则△ABC≌△DCE，
∴ AB＝DE，量出DE即得AB．(图略)
15．(1)连结AO并延长交⊙O于点E，连结EC，则∠E＝∠B．
∵ AE为⊙O直径，∴ ∠ECA＝90°，
在Rt△ECA中，sinE＝
，
∴ sinB＝
，∴ ＝2R．
(2)由命题结果得：
＝2R．
∴ R＝1，又∵ 
＝2．
∴ sinB＝
，∴ ∠B＝45°，
∴ ∠C＝180°-60°-45°＝75°．
16．本题答案不唯一，下面给出一种作法：
